Задание 2 огэ информатика

1.6. Дедуктивні висновки у логіці висловлювань

У логіці висловлювань правила висновку використовують, щоб виводити одні істинні речення з інших істинних речень. У коректному дедуктивному виведенні висновок з необхідністю випливає з посилок.

Означення 1.6.1. Логічним наслідком висловлювання є висловлювання 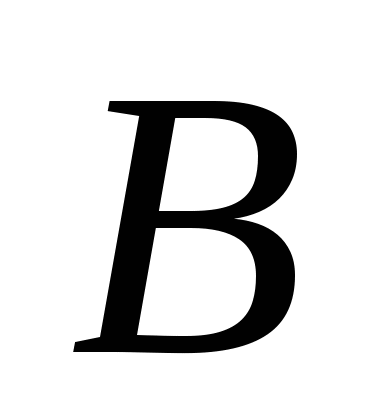, якщо формула є тотожно істинною. Це визначення може бути узагальнено для випадку висловлювань, якщо – тотожно істинна формула.

Приклад 1.6.1. Показати, що висловлювання 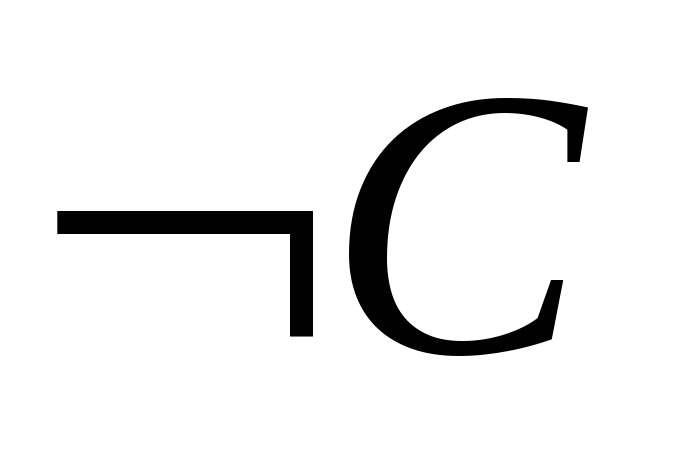є логічним наслідком висловлювання A\wedge  \urcorner C.

Розв’язання. Доведемо, що формула  A\wedge \urcorner C((A\wedge B)\vee \urcorner C) є загальнозначущою. Для її доведення використаємо тотожності логіки висловлювань та еквівалентні перетворення

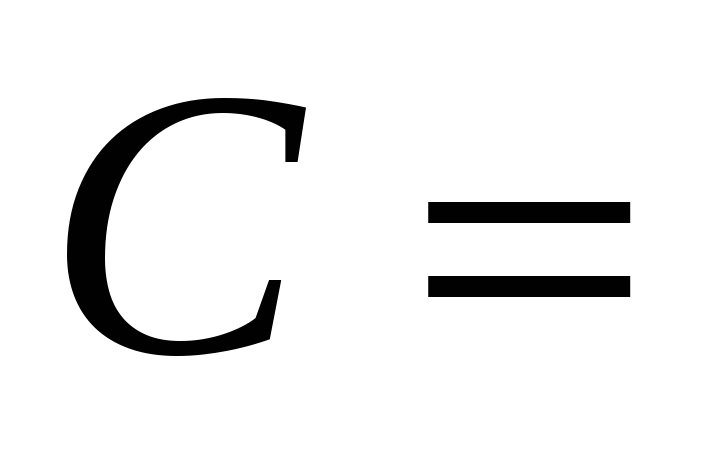
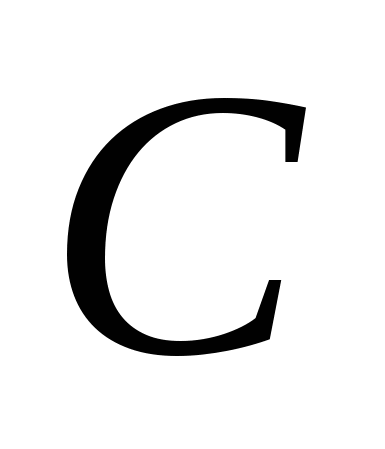
II.

Отже формула 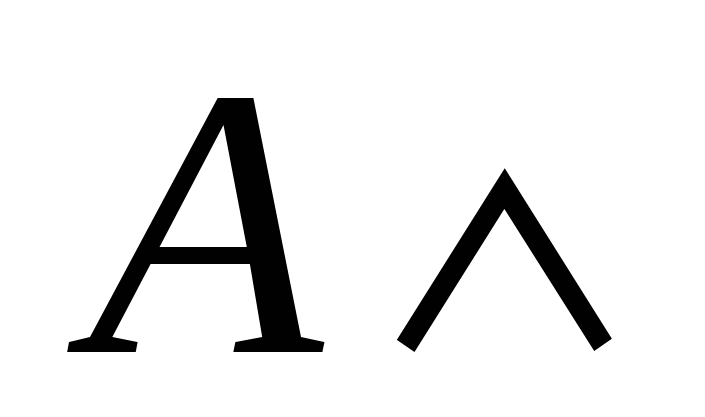є загальнозначущою, а за означенням 1.6.1 — логічний наслідок.

Означення 1.6.1. Дедуктивним висловлюванням називають висновок формули з формули , заснований на тому, що є логічним наслідком .

Приклад 1.6.2. Довести правильність міркування за дедукцією — “ Постанова кабинету Міністрів ухвалюється, якщо за неї голосує більшість міністрів. За постанову не проголосувала більшість міністрів, тому постанова не ухвалюється ”.

Розв’язання.До речень висловлювання введемо такі атоми :

A – “ за постанову проголосувала більшість міністрів ”;

B – “ постанова ухвалюється ”; A – “ за постанову не проголосувала більшість міністрів ”; B – “ постанова не ухвалюється ”;

Тоді засновки і висновки зазначимо відповідно через ~, , і приєднавши за допомогою імплікації до кон’юнкції засновків ~ висновок одержимо ~.

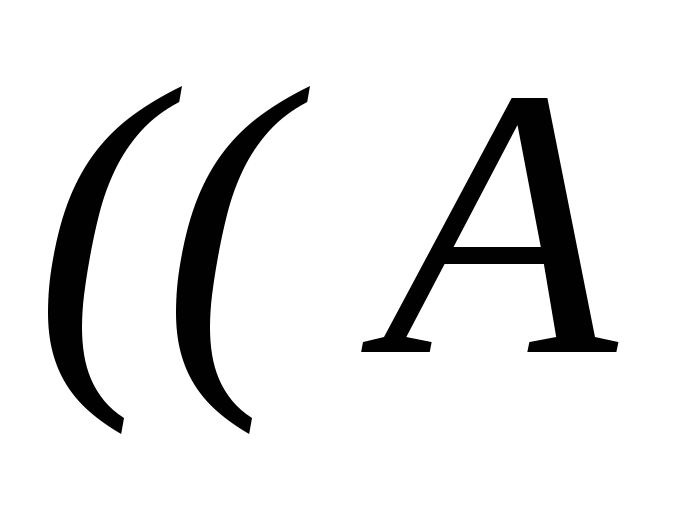Перевіримо за допомогою таблиці істинності, табл. 1.6.1., що задана імплікація ~ є логічним наслідком.

Таблиця 1.6.1

Із таблиці істинності слідує, що отримано тотожно істинне висловлювання. Отже, виходячи із законів, задане по умові міркування задовольняє визначення дедуктивного висновку. Таким чином, істинність висновку в дедуктивному висновку гарантується істинністю засновків.

Твердження 1.6.1. Висловлювання є логічним наслідком висловлювання , якщо висловлювання є тотожно хибним.

Твердження 1.6.2. Висловлювання є логічним наслідком висловлювання , якщо на всіх інтерпретаціях, на яких істинне, теж істинне.

Тотожна істинність або хибність засновків імплікації дозволяє зробити висновок про істинність або хибність наслідку.

Твердження 1.6.3 Якщо висловлювання є логічним наслідком висловлювання , а висловлювання – тотожно істинне висловлювання, то висловлювання також – тотожно істинне.

Твердження 1.6.4 Якщо висловлювання є тотожно хибним, то для будь-якого висловлювання правильно, що .

Правила для дедуктивного висновку будують на підставі загальнозначущих формул логіки висловлень виду .

Для наочного зображення правила умовиводів схематично записують за допомогою риски, над якою пишуть посилки, а під нею – висновок. Якщо посилок дві й більше, їх записують одну під одною ( табл. 1.6.2.)

Таблиця 1.6.2

Правильність всіх перелічених в табл. 1.6.2 логічних висловлювань можна довести за допомогою таблиць істинності. З усіх правил, наведених в табл. 1.6.2, найбільш часто використовується правило відділення. Правило відділення має такий логічний сенс, якщо засновок правильний, то правильний і наслідок із нього.

Приклад 1.6.3. Дано висловлювання “ Якщо n ділиться на 9, то n ділиться на 3 ”. Також відомо, що “n ділиться на 9”. Який висновок можна зробити, виходячи з ціх двох висловлювань?

Розв’язання. Введемо атомарні висловлювання

A – “ n ділиться на 9 ”,

B – “ n ділиться на 3 ”.

Висловлювання “ Якщо n ділиться на 9, то n ділиться на 3 ” можна записати у вигляді формули . З одночасного виконання засновків і можна зробити висновок за правилом відділення “ n ділиться на 3”.

Виды высказываний

Логические высказывания принято подразделять на составные (или сложные) и элементарные. Составные логические высказывания — высказывания, содержащие логические постоянные. Составные высказывания строятся на основе других высказываний. Логическое значение сложного высказывания определяется логическим значением входящих в его состав высказываний и теми логическими постоянными, с помощью которых оно построено.

Элементарные логические высказывания — это высказывания, не относящиеся к составным. Примером элементарного высказывания может служить 5<7{\displaystyle 5<7}. Примером составного логического высказывания может служить если 5<7{\displaystyle 5<7}, то 5{\displaystyle 5} — чётное число.

Примеры тавтологий

Тавтологии исчисления высказываний (и алгебры высказываний)

• A→A{\displaystyle A\rightarrow A} («Из A следует A») — закон тождества
• (A)∨(¬A){\displaystyle (A)\lor (\lnot A)} («A или не-A») — закон исключённого третьего
• ¬(P∧¬P){\displaystyle \neg (P\land \neg P)} — закон отрицания противоречия
• ¬¬P→P{\displaystyle \neg \neg P\rightarrow P} — закон двойного отрицания
• (PQ)(¬Q¬P){\displaystyle (P\leftrightarrow Q)\leftrightarrow (\neg Q\leftrightarrow \neg P)} — закон противоположности
• (P∧Q)(Q∧P){\displaystyle (P\land Q)\leftrightarrow (Q\land P)} — коммутативность конъюнкции
• (P∨Q)(Q∨P){\displaystyle (P\lor Q)\leftrightarrow (Q\lor P)} — коммутативность дизъюнкции
• (P∧Q)∧RP∧(Q∧R){\displaystyle \leftrightarrow } — ассоциативность конъюнкции
• (P∨Q)∨RP∨(Q∨R){\displaystyle \leftrightarrow } — ассоциативность дизъюнкции
• (P∧(P→Q))→Q{\displaystyle (P\land (P\rightarrow Q))\rightarrow Q}
• A→(B→A){\displaystyle A\rightarrow (B\rightarrow A)} (истина следует из чего угодно)
• A¬¬A{\displaystyle A\leftrightarrow \neg \neg A} (закон двойного отрицания)
• (A→B)∧(B→C)→(A→C){\displaystyle (A\rightarrow B)\wedge (B\rightarrow C)\rightarrow (A\rightarrow C)} — правило цепного заключения
• (A∨B)∧C(A∧C)∨(B∧C){\displaystyle (A\vee B)\wedge C\leftrightarrow (A\wedge C)\vee (B\wedge C)} — дистрибутивность конъюнкции относительно дизъюнкции
• (A∧B)∨C(A∨C)∧(B∨C){\displaystyle (A\wedge B)\vee C\leftrightarrow (A\vee C)\wedge (B\vee C)} — дистрибутивность дизъюнкции относительно конъюнкции
• (P∧P)P{\displaystyle (P\land P)\leftrightarrow P} — идемпотентность конъюнкции
• (P∨P)P{\displaystyle (P\lor P)\leftrightarrow P} — идемпотентность дизъюнкции
• (P→Q)(¬P∨Q){\displaystyle (P\rightarrow Q)\leftrightarrow (\neg P\lor Q)}
• (PQ)((PQ)∧(QP)){\displaystyle (P\leftrightarrow Q)\leftrightarrow ((P\leftrightarrow Q)\land (Q\leftrightarrow P))}
• (P∧(Q∨P)P{\displaystyle (P\land (Q\lor P)\leftrightarrow P} — первый закон поглощения
• (P∨(Q∧P)P{\displaystyle (P\lor (Q\land P)\leftrightarrow P} — второй закон поглощения
• ¬(A∧B)(¬A∨¬B){\displaystyle \neg (A\wedge B)\leftrightarrow (\neg A\vee \neg B)} — первый закон де Моргана
• ¬(A∨B)(¬A∧¬B){\displaystyle \neg (A\vee B)\leftrightarrow (\neg A\wedge \neg B)} — второй закон де Моргана
• (A→B)(¬B→¬A){\displaystyle (A\rightarrow B)\leftrightarrow (\neg B\rightarrow \neg A)} — закон контрапозиции
• Если ⊨F(X1,…,Xn){\displaystyle \vDash F(X_{1},…,X_{n})} и H1,…,Hn{\displaystyle H_{1},…,H_{n}} — формулы, то ⊨F(H1,…,Hn){\displaystyle \vDash F(H_{1},…,H_{n})} (правило подстановки)

Тавтологии исчисления предикатов (и алгебры предикатов)

• Если F(X1,…,Xn){\displaystyle F(X_{1},…,X_{n})} — тавтология в исчислении высказываний и P1,…,Pn{\displaystyle P_{1},…,P_{n}} — предикаты, то F(P1,…,Pn){\displaystyle F(P_{1},…,P_{n})} — тавтология в исчислении предикатов
• ¬(∀x)P(x)(∃x)¬P(x){\displaystyle \neg (\forall x)P(x)\leftrightarrow (\exists x)\neg P(x)}

¬(∃x)P(x)(∀x)¬P(x){\displaystyle \neg (\exists x)P(x)\leftrightarrow (\forall x)\neg P(x)} (закон де Моргана)

• (∀x)(P(x)∧Q(x))(∀x)P(x)∧(∀x)Q(x){\displaystyle (\forall x)(P(x)\wedge Q(x))\leftrightarrow (\forall x)P(x)\wedge (\forall x)Q(x)}
• (∃x)(P(x)∨Q(x))(∃x)P(x)∨(∃x)Q(x){\displaystyle (\exists x)(P(x)\vee Q(x))\leftrightarrow (\exists x)P(x)\vee (\exists x)Q(x)}
• Q(∃x)Q{\displaystyle Q\leftrightarrow (\exists x)Q}
• Q(∀x)Q{\displaystyle Q\leftrightarrow (\forall x)Q}
• (∀x)P(x)→P(y){\displaystyle (\forall x)P(x)\rightarrow P(y)}
• P(y)→(∃x)P(x){\displaystyle P(y)\rightarrow (\exists x)P(x)}
• (∀x)(∀y)P(x,y)(∀y)(∀x)P(x,y){\displaystyle (\forall x)(\forall y)P(x,y)\leftrightarrow (\forall y)(\forall x)P(x,y)}
• (∃x)(∃y)P(x,y)(∃y)(∃x)P(x,y){\displaystyle (\exists x)(\exists y)P(x,y)\leftrightarrow (\exists y)(\exists x)P(x,y)}
• (∃x)(∀y)P(x,y)→(∀y)(∃x)P(x,y){\displaystyle (\exists x)(\forall y)P(x,y)\rightarrow (\forall y)(\exists x)P(x,y)}

Аксиомы и правила вывода формальной системы логики высказываний

Одним из возможных вариантов (гильбертовской) аксиоматизации логики высказываний является следующая система аксиом:

A1A→(B→A){\displaystyle A_{1}:A\rightarrow (B\rightarrow A)};

A2(A→(B→C))→((A→B)→(A→C)){\displaystyle A_{2}:(A\rightarrow (B\rightarrow C))\rightarrow ((A\rightarrow B)\rightarrow (A\rightarrow C))};

A3A∧B→A{\displaystyle A_{3}:A\wedge B\rightarrow A};

A4A∧B→B{\displaystyle A_{4}:A\wedge B\rightarrow B};

A5A→(B→(A∧B)){\displaystyle A_{5}:A\rightarrow (B\rightarrow (A\wedge B))};

A6A→(A∨B){\displaystyle A_{6}:A\rightarrow (A\vee B)};

A7B→(A∨B){\displaystyle A_{7}:B\rightarrow (A\vee B)};

A8(A→C)→((B→C)→((A∨B)→C)){\displaystyle A_{8}:(A\rightarrow C)\rightarrow ((B\rightarrow C)\rightarrow ((A\vee B)\rightarrow C))};

A9¬A→(A→B){\displaystyle A_{9}:\neg A\rightarrow (A\rightarrow B)};

A10(A→B)→((A→¬B)→¬A){\displaystyle A_{10}:(A\rightarrow B)\rightarrow ((A\rightarrow \neg B)\rightarrow \neg A)};

A11A∨¬A{\displaystyle A_{11}:A\vee \neg A}.

вместе с единственным правилом:

A(A→B)B{\displaystyle {\frac {A\quad (A\rightarrow B)}{B}}} (Modus ponens)

Теорема корректности исчисления высказываний утверждает, что все перечисленные выше аксиомы являются тавтологиями, а с помощью правила modus ponens из истинных высказываний можно получить только истинные. Доказательство этой теоремы тривиально и сводится к непосредственной проверке. Куда более интересен тот факт, что все остальные тавтологии можно получить из аксиом с помощью правила вывода — это так называемая теорема полноты логики высказываний.
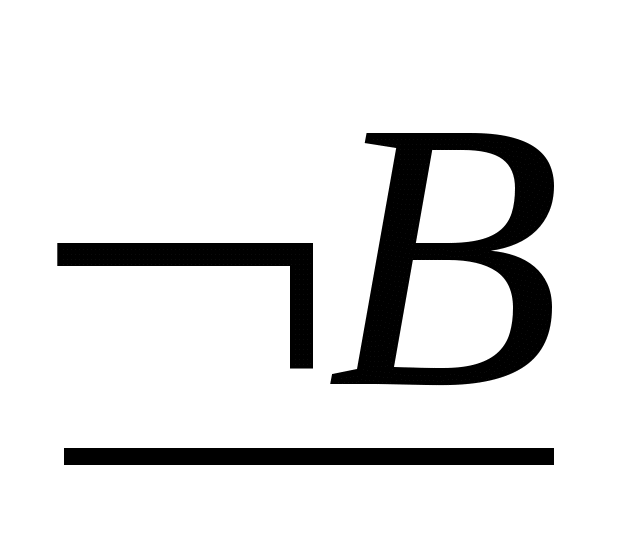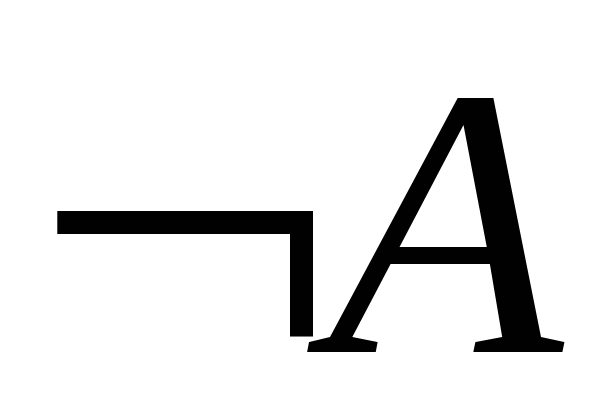
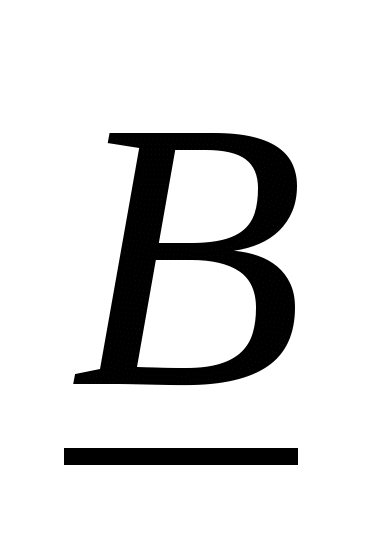