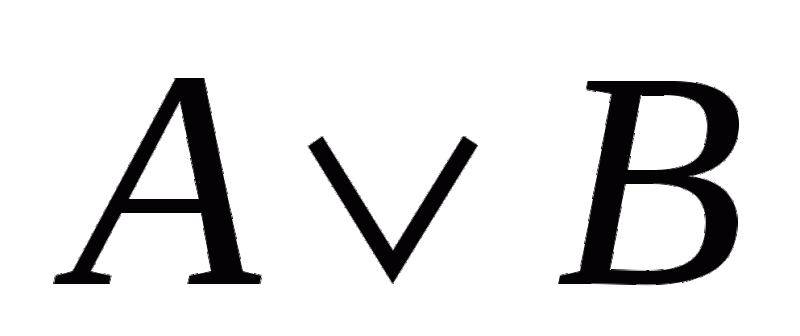Что такое истинное высказывание

Логическое уравнение

Данный термин используется в метаязыке. Под логическим уравнением можно представить запись F1=F2, в которой F1и F2 являются формулами расширенного языка логических высказываний. Решить такое уравнение означает, определить те наборы истинных значений переменных, которые будут входить в одну из формул F1 либо F2, при которых будет соблюдаться предложенное равенство.

Знак равенства в математике в некоторых ситуациях свидетельствует о равенстве исходных объектов, а в ряде случаев он ставится для демонстрации равенства их значений. Запись F1=F2 может свидетельствовать о том, что речь идет об одной и той же формуле.

В литературе довольно часто под формальной логикой подразумевают такой синоним, как «язык логических высказываний». В качестве «правильных слов» выступают формулы, служащие семантическими единицами, используемыми для построения рассуждений в неформальной (философской) логике.

Высказывание выступает в качестве предложения, которое выражает конкретное суждение. Иными словами, оно выражает мысль о присутствии некоего положения дел.

Любое высказывание можно будет считать истинным в том случае, когда положение дел, описываемое в нем, существует в реальности. В иных случаях такое высказывание будет являться ложным утверждением.

Данный факт стал основой пропозициональной логики. Существует подразделение высказываний на простые и сложные группы.

При формализации простых вариантов высказываний применяют элементарные формулы языка нулевого порядка. Описание сложных высказываний возможно только с применением формул языка.

Логические связки необходимы для обозначения союзов. При их применении простые высказывания превращаются в сложные виды:

• «не»,
• «неверно, что…»,
• «или».

Алгебра высказываний

Высказывание – повествовательное предложение, о котором можно сказать истинно оно или ложно. В алгебре простым высказываниям ставятся в соответствии логические переменные (А, В, С и т.д.)

Логическая переменная – это простое высказывание. Логические переменные обозначаются прописными и строчными латинскими буквами (a-z, A-Z) и могут принимать всего два значения – 1, если высказывание истинно, или 0, если высказывание ложно.

 Пример высказываний:

Логическая функция – это сложное высказывание, которое получается в результате проведения логических операций над простыми высказываниями.

Для образования сложных высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».Например,

Многие люди  не любят сырую погоду.

Пусть А = «Многие люди любят сырую погоду». Получаем логическую функцию F(A) = не А.

Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

Логическая формула (логическое выражение) — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА (1) или ЛОЖЬ (0).

Значение логической функции зависит от значений входящих в нее логических переменных. Поэтому значение логической функции можно определить с помощью специальной таблицы (таблицы истинности), в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.

                                                                      Основные (базовые) логические операции:

1. Логическое умножение (конъюнкция), от лат. konjunctio – связываю:•    Объединение двух (или нескольких) высказываний в одно с помощью союза И;•     в языках программирования — And. •    Принятые обозначения: /\ , •, и, and.•    В алгебре множеств конъюнкции соответствует операция пересечения множеств.  

Конъюнкция истинна тогда и только тогда, все, входящие в нее высказывания истинны.

Пример: Рассмотрим составное высказывание  «2 • 2 = 4 и 3 • 3 = 10». Выделим простые высказывания:А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)В = «3 • 3 = 10» = 0 (т.к. это ложное высказывание)Поэтому, логическая функция F(A, B) = A /\ B = 1 /\ 0 = 0 (в соответствии с таблицей истинности), то есть данное составное высказывание ложное.

2. Логическое сложение (дизъюнкция), от лат. disjunctio – различаю:•    Объединение двух (или нескольких) высказываний в одно с помощью союза ИЛИ;•     в языках программирования — Or. •    Обозначение:  \/, +, или, or.•    В алгебре множеств дизъюнкции соответствует операция объединения множеств.  

Дизъюнкция ложна тогда и только тогда, все, входящие в нее высказывания ложны.

Пример: Рассмотрим составное высказывание  «2 • 2 = 4 или 2 • 2 = 5». Выделим простые выска-зывания:А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)В = «2 • 2 = 5» = 0 (т.к. это ложное высказывание)Поэтому, логическая функция F(A, B) = A \/ B = 1 \/ 0 = 1 (в соответствии с таблицей истинности), то есть данное составное высказывание истинно.

3. Отрицание (инверсия), от лат. InVersion – переворачиваю:

•    Соответствует частице НЕ, словосочетаниям НЕВЕРНО, ЧТО или НЕ ЯВЛЯЕТСЯ ИСТИНОЙ, ЧТО;•    в языках программирования — Not; •    Обозначение: не А, ¬А, not•    В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества.

 
 
 
 
 
 
Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.

 Пример:

А = {два умножить на два равно четырем} = 1.

 ¬A= {Неверно, что два умножить на два равно четырем}= 0.

Рассмотрим высказывание А : «Луна — спутник Земли«;  тогда   ¬А будет формулироваться так:  «Луна — не спутник Земли«.

Рассмотрим высказывание: «Неверно, что 4 делится на 3». Обозначим через А простое высказывание «4 делится на 3». Тогда логическая форма отрицания этого высказывания имеет вид ¬А

Приоритет логических операций:

Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:     1. инверсия;     2. конъюнкция;     3. дизъюнкция;Для изменения указанного порядка выполнения логических операций используются круглые скобки.

Составные логические выражения алгебры высказываний называют формулами.Истинно или ложно значение формулы можно определить законами алгебры логики, не обращаясь к смыслу: F = (0 \/ 1) /\ (¬0 \/ ¬1) = (0 \/ 1) /\ (1 \/ 0) =1 /\ 1=1 — истинаF = (¬0 /\ ¬1) \/ (¬1 \/ ¬1) = (1 /\ 0) \/ (0 \/ 0) = 0 \/ 0 = 0 — ложь

Прямые и косвенные высказывания

Такие высказывания, переносный (прагматический) смысл которых отличается от буквального (семантического) содержания предложения, называются «косвенными» (в отличие от «прямых»).

Косвенное высказывание как предмет герменевтики

Извлечение прагматического смысла высказывания из семантического содержания предложения и разнообразие возможных прагматических интерпретаций одного предложения изучаются герменевтикой.

Косвенное высказывание как предмет риторики

Воплощение задуманного (исходного) прагматического смысла (замысла) в косвенном высказывании путём употребления предложения с иным (буквальным) семантическим содержанием и разнообразие экивоков — возможных способов иносказания (выбор средств «непрямого» выражения смысла на фоне множества прагматических эквивалентов, возможных в данной речевой обстановке) изучаются риторикой.

Виды высказываний

Логические высказывания принято подразделять на составные (или сложные) и элементарные. Составные логические высказывания — высказывания, содержащие логические постоянные. Составные высказывания строятся на основе других высказываний. Логическое значение сложного высказывания определяется логическим значением входящих в его состав высказываний и теми логическими постоянными, с помощью которых оно построено.

Элементарные логические высказывания — это высказывания, не относящиеся к составным. Примером элементарного высказывания может служить 5<7{\displaystyle 5<7}. Примером составного логического высказывания может служить если 5<7{\displaystyle 5<7}, то 5{\displaystyle 5} — чётное число.

Научное определение

С точки зрения науки высказывание – это основной (неопределяемый) термин из области математической логики. В более ходовом понимании высказывание представляет собой любое повествовательное предложение, которое утверждает что-либо о чем-либо. Причем с точки зрения конкретных обстоятельств и временных рамок можно с точностью заявить, является оно истинным или ложным в существующих условиях. Каждое подобное логическое высказывание можно отнести, таким образом, к одной из 2-х групп:

1. Истина.
2. Ложь.

К истинным высказываниям, например, принадлежат следующие:

• Если девушка окончила школу, она получает аттестат о среднем образовании.
• Лондон – столица Великобритании.
• Карась – рыба.

Ложные высказывания, например, такие:

• Собака — не животное.
• Санкт-Петербург построен на Москве-реке.
• Число 15 делится на 3 и 6.

Важные понятия для установления истинности или ложности высказывания

К основным терминам, которые так или иначе соприкасаются с областью логических высказываний, относятся:

• «суждение» – некоторое высказывание, которое потенциально является истинным или ложным;
• «утверждение» – суждение, которое требует доказательства или опровержения;
• «рассуждение» – совокупность логичных и взаимосвязанных суждений, фактов, умозаключений и положений, которые могут быть получены благодаря другим суждениям по определенным правилам вынесения вывода;
• «индукция» – способ рассуждения от частного (более мелкого) к общему (более глобальному);
• «дедукция» – наоборот, способ рассуждения от общего к частному (именно дедуктивным методом в преимуществе своем пользовался знаменитый герой рассказов Артура Конан Дойля Шерлок Холмс, который вкупе с базой знаний, наблюдательностью и внимательностью позволял ему находить истину, облекать её в форму логических высказываний, выстраивать правильные цепочки умозаключений и в результате устанавливать личность преступника).

Семантика логических знаков

Чтобы понять, для какого числа Х истинно высказывание, можно вооружиться таблицами истинности. Семантика логическая представляет раздел металогики, который исследует отношение к обозначаемым объектам, их содержанию разнообразных языковых выражений.

Данная проблема рассматривалась уже в античном мире, но в виде полноценной самостоятельной дисциплины она была сформулирована только на рубеже XIX—XX веков. Работы Г. Фреге, Ч. Пирса, Р. Карнапа, С. Крипке позволили выявить суть данной теории, ее реалистичность и целесообразность.

На протяжении длительного временного периода семантическая логика опиралась в основном на анализ формализованных языков. Только в последнее время большая часть исследований стала посвящаться естественному языку.

В данной методике выделяют две основные области:

• теорию обозначения (референции);
• теорию смысла.

Первая предполагает исследование отношения разнообразных языковых выражений к обозначаемым объектам. В качестве ее основных категорий можно представить: «обозначение», «имя», «модель», «интерпретация». Данная теория является основой для доказательств в современной логике.

Теория смысла занимается поиском ответа на вопрос относительно того, что представляет собой смысл языкового выражения. Она объясняет их тождественность по смыслу.

Существенную роль теория смысла имеет при обсуждении семантических парадоксов, при решении которых любой критерий приемлемости считается важным и актуальным.

Научное определение

С точки зрения науки высказывание – это основной (неопределяемый) термин из области математической логики. В более ходовом понимании высказывание представляет собой любое повествовательное предложение, которое утверждает что-либо о чем-либо. Причем с точки зрения конкретных обстоятельств и временных рамок можно с точностью заявить, является оно истинным или ложным в существующих условиях. Каждое подобное логическое высказывание можно отнести, таким образом, к одной из 2-х групп:

1. Истина.
2. Ложь.

К истинным высказываниям, например, принадлежат следующие:

• Если девушка окончила школу, она получает аттестат о среднем образовании.
• Лондон – столица Великобритании.
• Карась – рыба.

Ложные высказывания, например, такие:

• Собака — не животное.
• Санкт-Петербург построен на Москве-реке.
• Число 15 делится на 3 и 6.

Литература

• Бродский И. Н. Элементарное введение в символическую логику. — Издательство Ленинградского университета, 1972. — 63 с.
• Розенталь Д. Э., Теленкова М. А. Словарь-справочник лингвистических терминов. — 2-ое изд. — М.: Просвещение, 1976.
• Высказывание // Вешин — Газли. — М. : Советская энциклопедия, 1971. — ( :  / гл. ред. А. М. Прохоров ; 1969—1978, т. 5).
• Кондаков Н.И. Логический словарь. — 2-е изд. — М.: Наука, 1975. — 721 с.
• Чупахин И.Я.,Бродский И.Н. Формальная логика. — Ленинград: Издательство Ленинградского университета, 1977. — 357 с.
• Войшвилло Е. К., Дегтярев М. Г. Логика. — М.: ВЛАДОС-ПРЕСС, 2001. — 528 с. — ISBN 5-305-00001-7.
• Карпенко, А.С. Современные исследования в философской логике // Логические исследования. — М.: Наука, 2003. — Вып. 10. — С. 61—93. — ISBN 5-02-006257-X.
• Новая философская энциклопедия. — М., 2010. — Т. 2.

Формы высказываний

В логике предикатов высказывательной формой (формой высказывания, предикатом) называется неполное логическое высказывание, в котором один из объектов заменён предметной переменной. При подстановке вместо такой переменной какого-либо значения высказывательная форма превращается в высказывание. В качестве предметных переменных в естественном языке выступают общие имена, представляющие классы предметов и заменяемые в формализованных языках специальными символами. Форма сходна с высказыванием, однако она не истинна и не ложна (неопределенно-истинна), поскольку неизвестно, к чему относится утверждение или отрицание.

Форма высказывания требует дополнения, относится ли утверждение или отрицание в суждении ко всем или не ко всем предметам того класса, который представляет данное общее имя. Функцию таких указателей выполняют явно выраженные или подразумеваемые кванторы. Нельзя оценивать как истинное или ложное такую высказывательную форму, как Человек — справедлив. Приведённая фраза аналогична выражению y — справедлив. Из указанной формы можно получить высказывание, заменив общее имя единичным: Иванов — справедлив, или введя кванторы: Некоторые люди справедливы. Высказывания, использующие кванторы, выражают множественные — общие и частные — суждения.

1.1. Основные определения

Логика как самостоятельная наука возникла в IV веке до н.э. в трудах Аристотеля, который опираясь на накопленные до него знания, дополнил их собственными и создал систему формального логического вывода, которая заключается в том,  что в рассуждениях одни предложения исходят из других через определенную связь между их формой и структурой независимо от их содержания.

Революционные научные волнения конца XIX — начала ХХ века затронули и логику Аристотеля, путем реализации идеи Г. В. Лейбница , предложенной им еще в конце ХVII века , о применении в логике математической символики и построений логических исчислений . Эта идея реализована в работах Д. Буля , Ч.С. Пирса, Ф. Л. Г. Фреге , наряду со многими исследованиями других ученых.

Классическая математическая логика включает два основных раздела: логику высказываний и логику предикатов. Для их построения существуют два подхода ( языка ) , на основе которых основаны два варианта формальной логики: алгебра логики и логическое исчисление . Между основными понятиями этих языков имеет место взаимно однозначное соответствие, но строго говоря эти термины не синонимы.

Рисунок 1.1 – Составные части классической математической логики

По своей сути логика высказываний — это наука про размышления, предпосылки и выводы которых складываются из высказываний.

Определение 1.1.1. Высказыванием называют осмысленное выражение обычного языка,  которому можно приписать значения истинности.

Таким выражением может стать утверждение или повествовательное предложение, о котором можно сказать, истинное оно или ложное. Следует иметь в виду, что в логике высказываний нет средства, чтобы установить истинность или ложность простого высказывания. Если истинность и ложность нельзя установить вообще (то есть с помощью других наук), то такое высказывание не рассматривается (например: указательные высказывания, бессмысленные утверждения).

Определение 1.1.2. Значенние истинности – это абстрактный объект, которой ставится в соответтствии с высказыванием: истина – когда высказывание отвечает действительности, ложь – когда высказывание не отвечает действительности.

Обозначают : “Истина ” – И, T (True), или 1; “Ложь” – Л, F (False) або 0.

Пример 1.1.1. Определить какие из данных предложений являются выражениями:

“Днепр впадает в Черное море ”; “Днепр впадает в Азовское море ”; “Кто вы?”;

“Расстояние от Земли до Сонця равняется 150 млн км ”.

Решение. Первые два предложения являются высказываниями, причем первое является истинным, а второе – ложным высказыванием. Третье предложение не является высказыванием, поскольку оно не повествовательное. Четвертое предложение также не является высказыванием. Его истинность или ложность зависит от определенной точности.

Классическая логика высказываний оперирует  только двумя значениями истинности: И и Л, но не одновременно одним и другим, поэтому ее называют двузначной или бинарной логикой.

Повествовательные предложения могут быть простыми и сложными. Каждое простое предложение может быть утверждением и не может быть разбито на более мелкие предложения.

Определение 1.1.3. Атомом (элементарным высказыванием) называется такое высказывание, которое является простым повествовательным предложением, т.е. не имеет составных частей.

Для обозначения атомо используют, как символы, буквы латинского алфавита с индексами или без них.

Сложные предложения, как правило, состоят из простых предложений, соединенных союзами. То есть простые предложения, которые представляют атомы и союзы, являются элементами словаря, необходимого для формализации естественного языка с помощью логики высказываний. Значение истинности сложного высказывания определяется значениями истинности его составных частей.

Алгебра высказываний полностью абстрагуруется от смыслового значения высказываний,  принимая во внимание только их предметное значения, то есть денотат, которым выступают такие абстрактные объекты, как «истина» и «ложь». Определение 1.1.4. Интерпретацией высказыванийназывают приписывание значений истинности атомам, из которых построены высказывания

Определение 1.1.4. Интерпретацией высказыванийназывают приписывание значений истинности атомам, из которых построены высказывания.

Если высказывания содержат  n атомов, то можно составить  2n интерпретаций.

Определение 1.1.5. Однозначно определенным высказываниемназивают высказывания,  значение истинности которого не зависит от ситуации. Например, “33=9” = И. Но существуют высказывания, которые могут принимать разные значения. Например, “Завтра будет снег”, можно придавать значение “Истина ” и  “Ложь ” в зависимости от конкретной ситуации.

Классификация высказываний

Итак, если то, что такое высказывание, выяснено, то классификация этой категории остается всё ещё не определена. Между тем она действительно существует. Высказывания делятся на 2 две группы:

1. Простое, или элементарное, высказывание – это предложение, представляющее собой одно-единственное утверждение.
2. Сложное, или составное, высказывание, то есть такое, которое образовано из элементарных, благодаря использованию грамматических связок «или», «и», «ни», «не», «если… то…», «тогда и только тогда» и др. Примером может послужить истинное предложение: «Если у ребенка есть мотивация, то он хорошо занимается в школе», которое образовано из 2-х элементарных высказываний: «У ребёнка есть мотивация» и «Он хорошо занимается в школе» при помощи связующего элемента «если… то…». Аналогичным образом строятся все подобные конструкции.

Итак, с тем, что такое высказывание именно применительно к области точных наук, теперь всё ясно. Например, в алгебре любое высказывание рассматривается только в аспекте его логического значения, без учета какого бы то ни было житейского содержания. Здесь высказывание может быть или исключительно истинным, или исключительно ложным – третьего не дано. В этом логическое высказывание качественно отличается от высказывания философского, о котором будет сказано далее.

В школьной математике (а также подчас и информатике) элементарные высказывания обозначаются строчными буквами латиницы: a, b, c, … x, y, z. Истинное значение суждения традиционно отмечается цифрой «1», а ложное значение – цифрой «0».

Принцип многозначности

Если переформулировать вариант двухзначного высказывания для выявления истинности, можно превратить его в частный случай многозначности: любое высказывание будет иметь одно п значение истинности, если п равно либо больше 2, или же меньше бесконечности.

В качестве исключений дополнительных значений истинности (выше «ложно» и «истинно») выступают многие логические системы, базирующиеся на принципе многозначности. Двузначная классическая логика характеризует типичные варианты использования некоторых логически знаков: «или», «и», «не».

Многозначная логика, претендующая на их конкретизацию, не должна противоречить результатам двузначной системы.

Ошибочным считают то убеждение, согласно которому, принцип двузначности всегда приводит к констатации фатализма и детерминизма. Также неверна и мысль, согласно которой, многократную логику рассматривают в качестве необходимого средства осуществления индетерминистических рассуждений, что принятие ее соответствует отказу от использования строгого детерминизма.

Семантика логических знаков

Чтобы понять, для какого числа Х истинно высказывание, можно вооружиться таблицами истинности. Семантика логическая представляет раздел металогики, который исследует отношение к обозначаемым объектам, их содержанию разнообразных языковых выражений.

Данная проблема рассматривалась уже в античном мире, но в виде полноценной самостоятельной дисциплины она была сформулирована только на рубеже XIX—XX веков. Работы Г. Фреге, Ч. Пирса, Р. Карнапа, С. Крипке позволили выявить суть данной теории, ее реалистичность и целесообразность.

На протяжении длительного временного периода семантическая логика опиралась в основном на анализ формализованных языков. Только в последнее время большая часть исследований стала посвящаться естественному языку.

В данной методике выделяют две основные области:

• теорию обозначения (референции);
• теорию смысла.

Первая предполагает исследование отношения разнообразных языковых выражений к обозначаемым объектам. В качестве ее основных категорий можно представить: «обозначение», «имя», «модель», «интерпретация». Данная теория является основой для доказательств в современной логике.

Теория смысла занимается поиском ответа на вопрос относительно того, что представляет собой смысл языкового выражения. Она объясняет их тождественность по смыслу.

Существенную роль теория смысла имеет при обсуждении семантических парадоксов, при решении которых любой критерий приемлемости считается важным и актуальным.

Что такое высказывание в психологии: «Ты»-высказывание

Наука о человеческом сознании также отводит категории высказываний огромную роль. Именно с помощью неё индивид может произвести на окружающих положительное впечатление и создать неконфликтогенный микроклимат в отношениях. Поэтому сегодня психологи стараются популяризировать тему о наличии двух видов высказывания: это «Я»-высказывания и «Ты»-высказывания. Про последний тип любому, кто хочет совершенствоваться в общении, лучше навсегда забыть!

Характерными примерами «Ты»-высказывания являются такие:

• — Ты вечно не прав!
• — Опять ты лезешь со своими рекомендациями!
• — Ты можешь не быть таким неуклюжим?

В них сразу чувствуется открытое недовольство собеседником, обвинение, создание некомфортной для человека ситуации, в которой он вынужден защищаться. В этом случае он не может услышать, понять и принять точку зрения «обвинителя» потому, что изначально поставлен в положение противника и врага.

Логическое уравнение

Данный термин используется в метаязыке. Под логическим уравнением можно представить запись F1=F2, в которой F1и F2 являются формулами расширенного языка логических высказываний. Решить такое уравнение означает, определить те наборы истинных значений переменных, которые будут входить в одну из формул F1 либо F2, при которых будет соблюдаться предложенное равенство.

Знак равенства в математике в некоторых ситуациях свидетельствует о равенстве исходных объектов, а в ряде случаев он ставится для демонстрации равенства их значений. Запись F1=F2 может свидетельствовать о том, что речь идет об одной и той же формуле.

В литературе довольно часто под формальной логикой подразумевают такой синоним, как «язык логических высказываний». В качестве «правильных слов» выступают формулы, служащие семантическими единицами, используемыми для построения рассуждений в неформальной (философской) логике.

Высказывание выступает в качестве предложения, которое выражает конкретное суждение. Иными словами, оно выражает мысль о присутствии некоего положения дел.

Любое высказывание можно будет считать истинным в том случае, когда положение дел, описываемое в нем, существует в реальности. В иных случаях такое высказывание будет являться ложным утверждением.

Данный факт стал основой пропозициональной логики. Существует подразделение высказываний на простые и сложные группы.

При формализации простых вариантов высказываний применяют элементарные формулы языка нулевого порядка. Описание сложных высказываний возможно только с применением формул языка.

Логические связки необходимы для обозначения союзов. При их применении простые высказывания превращаются в сложные виды:

• «не»,
• «неверно, что…»,
• «или».

Логические постоянные

Логическая постоянная (логическая константа, логическая операция) — название термина, сохраняющего одно и то же значение во всех высказываниях и не зависящего от конкретного содержания высказывания. Логические постоянные используются для соединения простых высказываний в сложные. Логические постоянные делятся на кванторы и логические союзы (связки). Слова: не; неверно, что; и; или; если…, то; тогда и только тогда, когда; либо…, либо; несовместно; ни…, ни; не…, но; но и их ближайшие синонимы являются логическими связками, слова для всех…имеет место, что; для некоторых…имеет место, что и их ближайшие синонимы являются кванторами. Логические постоянные служат как для выражения мыслей в повседневных рассуждениях, так и в научных доказательствах.

В математической логике логические постоянные обозначаются следующими символами:

• ∀{\displaystyle \forall } — логические постоянные все, для всех…имеет место, что (квантор общности);
• ∃{\displaystyle \exists } — логические постоянные существует такой, что…, для некоторых…имеет место, что (квантор существования);
• ∧{\displaystyle \land }, &{\displaystyle \And } — союз и (конъюнкция);
• ∨{\displaystyle \vee } — союз или, когда он выступает в соединительно-разделительном значении (дизъюнкция);
• ∨˙{\displaystyle {\dot {\vee }}}, ∨∨{\displaystyle \vee \vee } — союз или, когда он выступает в строго-разделительном исключающем значении (строгая дизъюнкция);
• →{\displaystyle \rightarrow }, ⊃{\displaystyle \supset } — союз если…, то (импликация);
• ¬{\displaystyle \neg } — слова не, неверно (отрицание).

Логические союзы являются частью языка логики высказываний, кванторы были дополнительно введены в язык логики предикатов, который является расширением языка логики высказываний.

Пример высказывания

Как понять, для каких x истинно высказывание? Чтобы ответить на этот вопрос, используем выражение: «Частица а находится в области пространства b». Рассмотрим для этого высказывания следующие случаи:

• невозможно наблюдать частицу;
• можно наблюдать частицу.

Второй вариант предполагает определенные возможности:

• частица реально находится в определенной области пространства;
• ее нет в предполагаемой части пространства;
• частица движется так, что сложно определить область ее расположения.

В данном случае можно использовать четыре термина значений истинности, которые соответствуют приведенным возможностям.

Для сложных структур уместно использование большего количества терминов. Это свидетельствует о неограниченности значений истинности. Для какого числа истинно высказывание, зависит от практической целесообразности.

Заключение

Формальная логика помогает выяснять, для какого имени истинно высказывание, предполагает конструирование и анализ правил преобразования определенных выражений, которые сохраняют их истинное значение независимо от содержания. В качестве отдельного раздела философской науки она появилась только в конце девятнадцатого века. Вторым направлением является неформальная логика.

Основной задачей этой науки является систематизация правил, которые позволяют выводить новые утверждения на основе доказанных утверждений.

Фундаментом логики является возможность получения каких-то идей в качестве логического следствия иных утверждений.

Подобный факт позволяет адекватно описывать не только определенную проблему в математической науке, но и переносить логику в художественное творчество.

Логическое исследование предполагает отношение, которое существует между посылками и заключениями, выводимыми из них.

Его можно отнести к числу исходных, фундаментальных понятий современной логики, которую часто именуют наукой «что из него следует».

Сложно представить себе без подобных рассуждений доказательство теорем в геометрии, объяснение физических явлений, пояснение механизмов протекания реакций в химии.