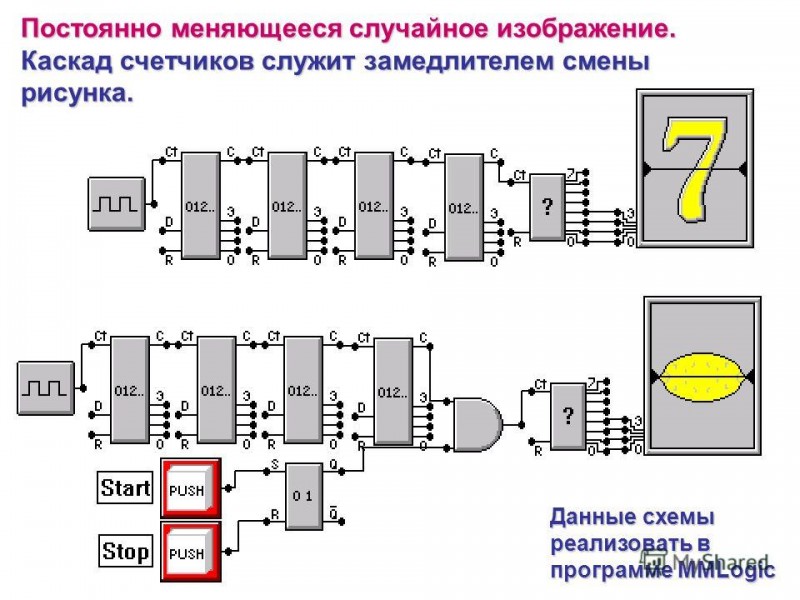
Урок 11упрощение логических выражений§21. упрощение логических выражений

Законы алгебры логики

Для упрощения логических выражений используют законы алгебры логики. Они формулируются для базовых логических операций — «НЕ», «И» и «ИЛИ».

Закон двойного отрицания означает, что операция «НЕ» обратима: если применить ее два раза, логическое значение не изменится. Закон исключённого третьего основан на том, что в классической (двузначной) логике любое логическое выражение либо истинно, либо ложно («третьего не дано»). Поэтому если А = 1, то А = 0 (и наоборот), так что произведение этих величин всегда равно нулю, а сумма — единице.

Операции с константами и закон повторения легко проверяются по таблицам истинности операций «И» и «ИЛИ». Переместительный и сочетательный законы выглядят вполне привычно, так же, как и в арифметике. Почти везде «работает» аналогия с алгеброй чисел, нужно только помнить, что в логике 1 + 1 = 1, а не 2.

Распределительный закон для операции «ИЛИ» — это обычное раскрытие скобок. А вот для операции «И» мы видим незнакомое выражение, в алгебре чисел это равенство неверно. Доказательство можно начать с правой части, раскрыв скобки:

(А + В) • (А + С) = А • А + А • С + В • А + В • С.

Дальше используем закон повторения (А • А = А) и заметим, что

А + А • С = А • (1 + С) = А • 1 = А.

Аналогично доказываем, что А + В • А = А • (1 + В) = А, таким образом,

(А + В) • (А + С) = А + В • С.

Равенство доказано. Попутно мы доказали также и закон поглощения для операции «И» (для операции «ИЛИ» вы можете сделать это самостоятельно). Отметим, что из распределительного закона следует полезное тождество:

А + А • В = (А + А ) • (А + В) = А + В.

Правила, позволяющие раскрывать отрицание сложных выражений, названы в честь шотландского математика и логика Огастеса (Августа) де Моргана

Обратите внимание, что при этом не просто «общее» отрицание переходит на отдельные выражения, но и операция «И» заменяется на «ИЛИ» (и наоборот). Доказать законы де Моргана можно с помощью таблиц истинности

Теперь с помощью приведённых законов алгебры логики упростим полученное ранее логическое выражение для объединения областей 3 и 4 на диаграмме с тремя переменными (§ 20, рис. 3.15):

(А • В • C ) + А • В • C = (А + А ) • В • C = В • C .

Здесь мы сначала вынесли общий множитель двух слагаемых за скобки, а затем применили закон исключённого третьего.

В общем случае можно рекомендовать такую последовательность действий.

1. Заменить все «небазовые» операции (исключающее ИЛИ, импликацию, эквивалентность и др.) на их выражения через базовые операции «НЕ», «И» и «ИЛИ».

2. Раскрыть отрицания сложных выражений по законам де Моргана так, чтобы операции отрицания остались только у отдельных переменных.

3. Используя вынесение общих множителей за скобки, раскрытие скобок и другие законы алгебры логики, упростить выражение.

(А + B ) • ( А + B ) • ( А + С)=(А + B ) • А • B • ( А + C = (А • А + B • А ) • B • ( А + С) = B • А • B • ( А + С) = А • B • B • ( А + С) = B • А • ( А + С) = B • ( А .

Здесь последовательно использованы закон де Моргана, распределительный закон, закон исключённого третьего, переместительный закон, закон повторения, снова переместительный закон и закон поглощения.

Следующая страница Логические уравнения

Cкачать материалы урока

Инструкция . При вводе с клавиатуры используйте следующие обозначения:

Клавиша	Оператор
!	¬	Отрицание (НЕ)
|	|	Штрих Шеффера (И-НЕ)
#	↓	Стрелка Пирса (ИЛИ-НЕ)
*	&	Конъюнкция (И)
+	v	Дизъюнкция (ИЛИ)
^	⊕	Исключающее ИЛИ, сумма по модулю 2 (XOR)
@	→	Импликация (ЕСЛИ-ТО)
%	←	Обратная импликация
=	≡ (

, )

Эквивалентность (РАВНО)

bc необходимо ввести так: a*b*c+a*b=c+a=b*c Для ввода данных в виде логической схемы используйте этот сервис.

Правила ввода логической функции

1. Вместо символа v (дизъюнкция, ИЛИ) используйте знак + .
2. Перед логической функцией не надо указывать обозначение функции. Например, вместо F(x,y)=(x|y)=(x^y) необходимо ввести просто (x|y)=(x^y) .
3. Максимальное количество переменных равно 10 .

Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2 N строк, так как существует 2 N различных комбинаций возможных значений аргументов.

Наука логика

Основы логики – это довольно непростой предмет, по нему написано очень много томов. В данной статье будут рассмотрены азы и законы преобразования логических выражений, то есть информация будет максимально сжатой и концентрированной. Это необходимо для рассмотрения более осмысленно компьютерных технологий и построения схем.

Для начала что такое логика и зачем она нужна? Важно отметить, что это целая наука, которая рассматривает формы и способы рассуждения. Все, что мы видим, слышим или делаем, подчиняется законам

Бросили мяч с высоты — он обязательно летит вниз, так как подчиняется законам физики. Завариваем утром ароматный кофе, добавляем сахар, а сыпучие вещества моментально растворяются в воде, подчиняясь законам физики. Мы ведем беседу с друзьями, делимся своими планами: «Если я хорошо защищу работу, то получу красный диплом», «У меня не получится приехать на машине, так как она находится в ремонте». Не замечая, мы строим все наши разговоры, опираясь именно на логику и ее законы. Так зачем нужна наука логика? Конечно, зная ее законы, вы сможете безошибочно определять исход какого-либо события, так как не придется действовать наугад и рисковать.

Хоть мышление является довольно сложным процессом, тем не менее можно его разделить на некие составляющие, точнее, формы (с помощью чего происходит выражение мысли):

• понятия;
• высказывания;
• умозаключения;
• доказательства.

Далее предлагаем вам перейти к логическим функциям и преобразованию логических выражений. Информатика окажется для вас веселым и довольно простым предметом, если внимательно читать данную статью.

Упрощение логических выражений

Для написания любой логической функции может быть использовано логическое выражение, после чего можно составить логическую схему. Как правило, все логические выражения упрощают для получения максимально простой и дешевой логической схемы. В сущности, логическая схема, выражение и логическая функция, являются тремя различными языками, повествующими об одном и том же.

Логические выражения упрощают при помощи различных законов алгебры логики. Часть преобразований напоминает преобразования формул, выполняемые в классической алгебре (например, применение сочетательного и переместительного законов, вынесение за скобки равенства общего множителя и так далее). Для других преобразований используют свойства, которых лишены операции классической алгебры.

Любые законы алгебры логики выводят для главных логических операций следующим образом: НЕ – инверсия (то есть, отрицание); ИЛИ – дизъюнкция (то есть, логическое сложение); И – конъюнкция (то есть, логическое умножение).

Закон двойного отрицания состоит в том, что операция НЕ является обратимой: если ее использовать два раза, логическое значение в результате останется неизменным.

Сущность закона исключенного третьего состоит в том, что каждое логическое выражение при любых условиях является истинным, либо ложным. Если A=1, тогда A=0, а также наоборот. Конъюнкция данных величин всегда равняется 0, дизъюнкция равна 1.

Закон повторения и операции с константами легко можно проверить, используя таблицы истинности операций ИЛИ и И.

Сочетательный и переместительный законы имеют такой же вид, как в математике. Аналогия с привычной всем классической алгеброй.

(A+B)⋅(A+C)=A⋅A+A⋅C+B⋅A+B⋅C

Используем закон повторение, гласящий, что A⋅A=A,

Затем A⋅A+C⋅A=A+C⋅A=A⋅(1+C)=A⋅1=A

A+A⋅B=A⋅(1+B)=A⋅1=A, следовательно, (A+B)⋅(A+C)=A+B⋅C.

Мы доказали равенство.

Правил, используемые для раскрытия инверсии сложных выражений, назвали именем известного логика и математика де Моргана. Суть состоит в том, что общее отрицание не только распространяется на отдельные выражения, а еще и дизъюнкция заменяется конъюнкцией (а также наоборот). Для доказательства данных правил используются таблицы истинности.

Основная часть аксиом и законов алгебры логики записаны попарно. Внимательно изучая пары, можно сформулировать принцип двойственности, звучащий следующим образом: если осуществить в тождестве замены конъюнкции, а также дизъюнкции. И также элементов 1 и 0 (при их наличии), получится тождество. Данное свойство именуют принципом двойственности.

Упрощения логических выражений в примерах

Формула, вытекающая из распределительного закона. При ее выведении применили вышеупомянутое правило де Моргана для дизъюнкции, а также использовали закон двойного отрицания, после чего сомножитель X, вынесли за скобку, тогда как в скобках получили закон исключённого третьего, а также применили операцию с константами.

Пример первый

Кто из рабочих, обозначенных, как A, B, C, D работает на заводе, а кто нет, если нам даны следующие условия:

• если работает A либо работает B, тогда не работает C;
• если не работает B, тогда работает D, а также работает C.

Решение задачи. Обозначим несколько простых высказываний:

1. A рабочий A на заводе работает;
2. B рабочий B на заводе работает;
3. C рабочий C на заводе работает;
4. D рабочий D на заводе работает.

Сформулировав данные из условия при помощи этих простых высказываний, получим следующее:

Получаем следующую конъюнкцию: ((A+B)→C)⋅(B→C⋅D)⋅C.

После упрощения данной формулы получаем, что A равно 0, B равно 1, C равно 1, D равно 1.

Ответ: ученик A на заводе не работает, а ученики B, C, D играют.

В этом примере применено правило де Моргана, затем использован распределительный закон, после этого применен закон исключенного третьего, потом использован переместительный закон. За ним реализован закон повторения, потом опять применен переместительный закон и, наконец, использован закон поглощения.

Чтобы отыскать решения логического уравнения можно также применить упрощение логических выражений.

Нужно отыскать все решения данного уравнения

Применив правило де Моргана, получим

B+C+A¯+A¯⋅C¯+D=0

а затем применяем закон поглощения и получаем

B+C+A¯+D=0

Чтобы логическая сумма равнялась нулю, все слагаемые должны равняться нулю, из чего следует, что

A равно 1, B равно 0, C равно 0, D равно 0.

Логические выражения и таблица истинности

Примеры задач с решениями по этой теме Пройти тестирование по теме Контрольная по теме

 Таблица истинности — таблица, показывающая,  какие значения принимает составное высказывание при  всех сочетаниях (наборах)  значений  входящих в него простых высказываний.

Логическое выражение — составные высказывания в виде формулы.

Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».

Алгоритм построения  таблицы  истинности:

1.подсчитать количество переменных n в логическом выражении;

2. определить число строк в таблице по формуле m=2n, где n — количество переменных;

3. подсчитать количество логических операций в формуле;

4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;

5. определить количество столбцов: число переменных + число операций;

6. выписать наборы входных переменных;

7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.

Заполнение таблицы:

1.разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;

2.разделить колонку  значений  второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;

3.продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.

Пример 1. Для формулы  A/\ (B \/ ¬B /\¬C) постройте  таблицу истинности.

 Количество логических переменных 3, следовательно, количество строк — 23 = 8.

Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.

Пример 2. Определите истинность  логического выражения  F(А, В) = (А\/ В)/\(¬А\/¬В) .

1. В выражении две переменные А и В (n=2).

2.  m_строк=2n, m=22=4 строки.

3. В формуле 5 логических операций.

4. Расставляем порядок действий

1) А\/ В;  2) ¬А;  3) ¬В;  4) ¬А\/¬В;  5) (А\/ В)/\(¬А\/¬В).

5. К_{столбцов}=n+5=2+5=7 столбцов.

А	В	А\/ В	¬А	¬В	¬А\/¬В	F
1	1	1
1	1	1	1	1
1	1	1	1	1
1	1	1

 Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.

Пример 3. Построёте таблицу истинности для логического выражения

F = (A\/ B) /\ ¬С

1. В данной функции три логические переменные – А, В, С
2. количество строк таблицы = 23 =8
3. В формуле 3 логические операции.
4. Расставляем порядок действий

1) А\/ В;  2) ¬С; 3) (AVB) /\ ¬С  .

1. количество столбцов таблицы = 3 + 3 = 6

А	В	С	A\/B	¬С	(A\/B) /\ ¬С
1
1
1	1	1	1
1	1	1
1	1	1	1
1	1	1
1	1	1	1	1
1	1	1	1

Пример 4.  Определите истинность формулы: F = ((С \/В) =>  В) /\ (А /\ В) => В.

Построим таблицу истинности этой формулы.

Ответ: формула является тождественно истинной.

Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.

Дан фрагмент таблицы истинности выражения F:

X	Y	Z	F
1
1
1	1

Какое выражение соответствует F?

 1) ¬X/\¬Y/\Z                      2) ¬X\/¬Y\/Z                  3) X\/Y\/¬Z              4) X\/Y\/Z

 Решение (вариант 1, через таблицы истинности):

Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:

X	Y	Z	F	¬X	¬Y	¬Z	¬X/\¬Y/\Z	¬X\/¬Y\/Z	X\/Y\/¬Z	X\/Y\/Z
1	1	1	1	1	1
1	1	1	1	1	1
1	1	1	1	1	1	1

 Очевидно, что значения заданной функции F совпадают со значениями выражения X\/Y\/¬Z. Следовательно, правильный ответ – 3.

Ответ: 3

 Решение (Вариант 2):

Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y  и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.

 Рассмотрим данный конкретный пример:

1)первое заданное выражение  ¬X/\¬Y/\Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;

2)второе заданное выражение ¬X\/¬Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует  второй строке таблицы;

3)третье выражение   X\/Y\/¬Z    соответствует F при всех предложенных комбинациях X,Y и Z;

4)четвертое выражение X\/Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.

Ответ: 3

Логические уравнения

Если приравнять два логических выражения, мы получим уравнение. Его решением будут значения переменных, при которых уравнение превращается в истинное равенство, т. е. когда значения левой и правой частей совпадают. Например, уравнение А • В = 1 имеет единственное решение: А = В = 1, для остальных комбинаций значений переменных левая часть равна нулю. В то же время уравнение А + В = 1 имеет три решения: (А = 0, В = 1), (А = 1, В = 0) и А = В = 1.

Пример 1. Требуется найти все решения уравнения

((B + C • А) → (А • C + D) = 0.

Вспоминаем, что импликация равна нулю только тогда, когда первое выражение равно 1, а второе — 0. Поэтому исходное уравнение сразу разбивается на два:

(B + C) • А = 1,       А • C + D = 0.

Первое уравнение с помощью закона де Моргана можно преобразовать к виду В • C • А = 1, откуда сразу следует, что все три сомножителя должны быть равны 1. Это значит, что А = 1, В = 0 и С = 0. Кроме того, из второго уравнения следует, что В=0. А=1 и С = 0 удовлетворяют и второму уравнению тоже. Решение найдено, причём оно единственное.

Возможен второй вариант — упростить выражение. Заменяя импликацию по формуле А → В = А + В получаем:

(B + C) • A + А • C + D = 0.

Используем закон де Моргана:

B + C + А + А • C + D = 0.

и закон поглощения:

В + С + А + D =0.

Для того чтобы логическая сумма была равна нулю, каждое слагаемое должно быть равно нулю, поэтому А = 1, В = С = D = 0.

Есть и третий вариант — построить таблицу истинности выражения в левой части и найти все варианты, при которых оно равно 0. Однако таблица истинности выражения с четырьмя переменными содержит 24 = 16 строк, поэтому такой подход достаточно трудоёмок.

Пример 2. Требуется найти все решения уравнения

(А + В) → (В • С • D) = 1.

Преобразуем выражение, раскрыв импликацию через операции «НЕ» и «ИЛИ» и применив закон де Моргана:

А + В + В • С • D = А • В + В • С • D= 1.

Если логическая сумма равна 1, то хотя бы одно слагаемое равно 1 (или оба одновременно).

Равенство А • В = 1 верно при А = 0, В = 1 и любых С и В. Поскольку есть всего 4 комбинации значений С и D, уравнение А • В = 1 имеет 4 решения:

Второе уравнение, B • C • D=1, даёт В = С = D = 1 при любом А, т. е. оно имеет два решения:

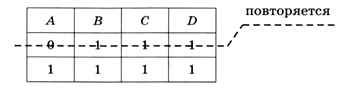
Видим, что первое из этих решений уже было получено раньше, поэтому уравнение имеет всего пять разных решений. Заметим, чтс^определить все повторяющиеся решения можно из уравнения (А • В) • (B • C • D) = 1, которое имеет единственное решение А = 0, В = С = D = 1.

Пример 3. Требуется найти число решений уравнения

A • B • C + B • C • D = 0..

Здесь, в отличие от предыдущих задач, не нужно находить сами решения, интересует только их количество. Уравнение распадается на два:

A • B • C = 0       и       B • C • D = 0.

Каждое из них имеет достаточно много решений. Можно поступить следующим образом: сначала найти количество решений «обратного» уравнения, с единицей в правой части:

A • B • C + B • C • D = 1

и затем вычесть его из 16 (общего количества комбинаций четырёх переменных). Уравнение А • В • С = 1 имеет два решения: А = В = С = 1 и любое D (0 или 1). Второе
уравнение, B • C • D = 1, тоже имеет два решения: А — любое, В = С = О, D = 1. Среди этих четырёх решений нет повторяющихся, поэтому исходное уравнение имеет 16 — 4 — 12 решений.

Пример 4. Требуется найти число решений уравнения

(Х₁ → Х₂) • (Х₂ → Х₃) • (Х₃ → Х₄) • (Х₄ → Х₅) • (Х₅ → Х₆) = 1.

Так как каждая логическая переменная может принимать только значения 0 и 1, можно представить решение в виде 6-битной цепочки. Например, цепочка 010110 означает, что Х₁ = Х₃ = Х₆ = 0 и Х₂ = Х₄ = Х₅ = 1.

Заметим, что импликация А → В ложна тогда и только тогда, когда А = 1 и В = 0. Поэтому в решении заданного уравнения не может встречаться последовательность 10, иначе какая-то импликация оказывается ложной и всё выражение будет равно 0. Поэтому существует всего 7 решений:

000000 000001 000011 000111 001111 011111 111111.

Обратите внимание, что число решений логических уравнений, в отличие от «обычных уравнений», всегда конечно. Это связано с тем, что каждая переменная может принимать только два значения (0 и 1), и число разных комбинаций значений переменных конечно, оно равно 2n, где n — это количество переменных

Поэтому уравнение с n переменными имеет не более 2n решений.

Подготовьте сообщение
а) «Законы логики и правила алгебры: сходство и различия»
б) «Методы решения логических уравнений»
в) «Системы логических уравнений»

Следующая страница Задачи

Cкачать материалы урока

Таблицы истинности

Выделяют следующие общие свойства, характерные всякой таблице:

• уже упомянутое число строк, вдвое превышающее количество переменных;
• число столбцов таблицы на один превышает количество задействованных переменных.

Вне зависимости от того, каково множество значений переменных, заданное в условии, всегда можно сформулировать такое выражение, которое будет равняться единице на определенном наборе переменных.

Записывается это как «дизъюнкция конъюнкций». На практике это означает, что можно построить некоторое выражение, имея перед собой готовую таблицу истинности. Конечно, объемы этой таблицы могут существенно усложнить задачу математика.

Необходимые знания и умения

Вне зависимости от сложности вычислений при решении любого выражения важно соблюдать порядок выполнения операций с числами:

1. скобки;
2. возведение в степень;
3. умножение;
4. деление;
5. сложение;
6. вычитание.

Последние два пункта можно спокойно поменять местами и это никак не отразится на результате. Но складывать два соседних числа, когда рядом с одним из них стоит знак умножения категорически нельзя! Ответ если и получится, то неверный. Поэтому нужно запомнить последовательность.

Применение подобных

К таким элементам относятся числа с переменной одного порядка или одинаковой степени. Существуют и так называемые свободные члены, не имеющие рядом с собой буквенного обозначения неизвестного.

Суть заключается в том, что при отсутствии скобок можно упростить выражение, складывая или вычитая между собой подобные.

Разложение числа на множители

Эта маленькая математическая хитрость, если научиться её правильно использовать, в будущем не раз поможет справиться с каверзной задачкой. Да и понять, как работает «система», несложно: разложением называют произведение нескольких элементов, вычисление которого даёт исходное значение. Таким образом, 20 можно представить как на 20×1, 2×10, 5×4, 2×5×2 или другим способом.

Проделывать такую операцию можно как со свободными членами, так и с цифрами при переменной. Главное, не потерять последнюю во время вычислений — даже после разложения неизвестная не может взять и «уйти в никуда». Она остаётся при одном из множителей:

• 15x=3(5x);
• 60у2=(15y2)4.

Простые числа, которые можно разделить лишь на себя или 1, никогда не раскладываются — в этом нет смысла.