Тренажер для изучения логических элементов

Определения и понятия

Под таблицей истинности понимают свод значений, которые может принять высказывание при сочетании различных входящих комбинаций. Другими словами, каждому набору функций или сигналам, присутствующим на входе чего-либо, соответствует строго определённые показатели на выходе. Все значения, являющиеся всевозможными высказываниями, называют логическими выражениями. Если в таблице последние столбцы логичных выражений идентичны, то рассматриваемый объект считается равносильным.

Любое выражение можно описать формулой, в которую будут включаться переменные, характеризующие состояния, и обозначающие функции знаки логических операций. Поэтому используя язык математики, в частности, алгебры, любое сложное высказывание можно разделить на несколько простых, а затем объединить логической связью.

Применение двух цифр подчёркивает соответствие между двоичной системой счисления и математической логикой. В итоге с помощью последней стало удобным описывать работу цифровых схем радиоэлектронной аппаратуры, алгоритмы в программировании, проводить синтез и анализ результата выполнения операций.

Суждение о правильности построения таблиц истинности для логических выражений основано на учёте всех переменных и операций, последовательно выполняющихся в рассматриваемой функции. Обычно для начертания используют 2n 1 строк, где n обозначает количество входных переменных, и n m столбцов, m — число значений на выходе.

CIRCUIT LAB

Circuit Lab – это многофункциональный онлайн-симулятор схем, но он не бесплатный. Он разработан с простым в использовании редактором и точным аналоговым / цифровым схемным симулятором.

Преимущества Circuit Lab:

• Эта платформа хорошо выполнена и имеет довольно обширную библиотеку, которая подходит как для начинающих, так и для опытных экспериментаторов
• Смоделированные графики и выходные результаты можно экспортировать в виде файла CSV для дальнейшего анализа
• Проектирование цепей выполняется легко, и доступны предварительно разработанные схемы

Недостатки Circuit Lab:

• Это не бесплатная платформа, но вы можете использовать демонстрационную версию бесплатно
• Моделирование могло бы быть лучше с интерактивными симуляциями кроме графического представления
• Больше цифровых микросхем следовало бы добавить в библиотеку

Презентация на тему: » Логический конструктор MMLogic (продолжение) Программа для моделирования логических и физических элементов компьютера Глезденев В.И. учитель информатики.» — Транскрипт:

1

Логический конструктор MMLogic (продолжение) Программа для моделирования логических и физических элементов компьютера Глезденев В.И. учитель информатики выс. квал. кат.

2

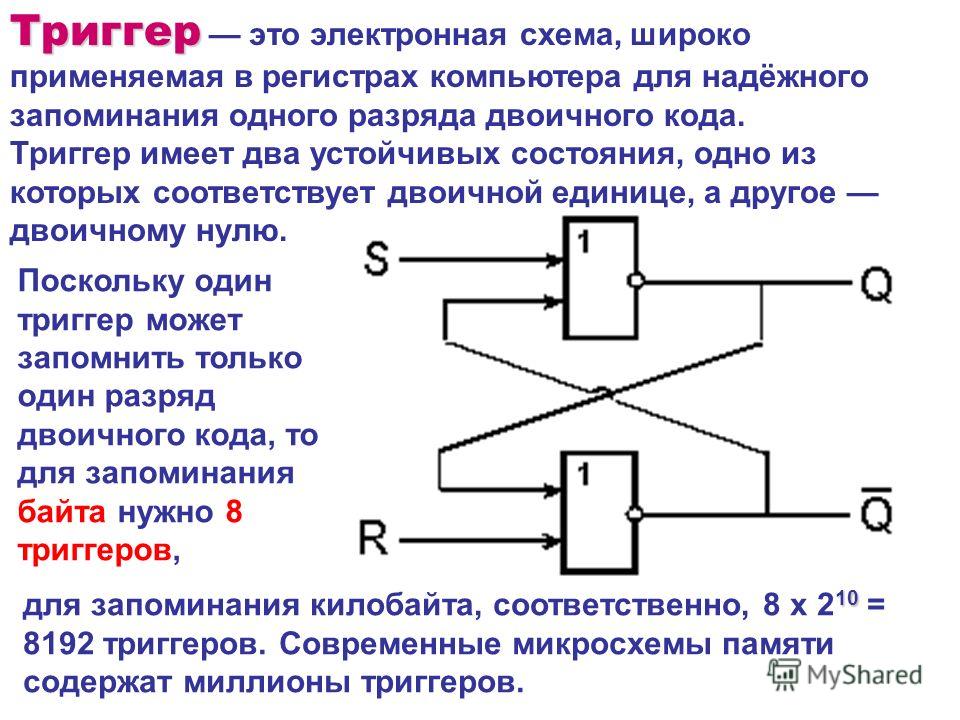
Триггер Триггер это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое двоичному нулю. Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, 10 для запоминания килобайта, соответственно, 8 х 2 10 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.

3

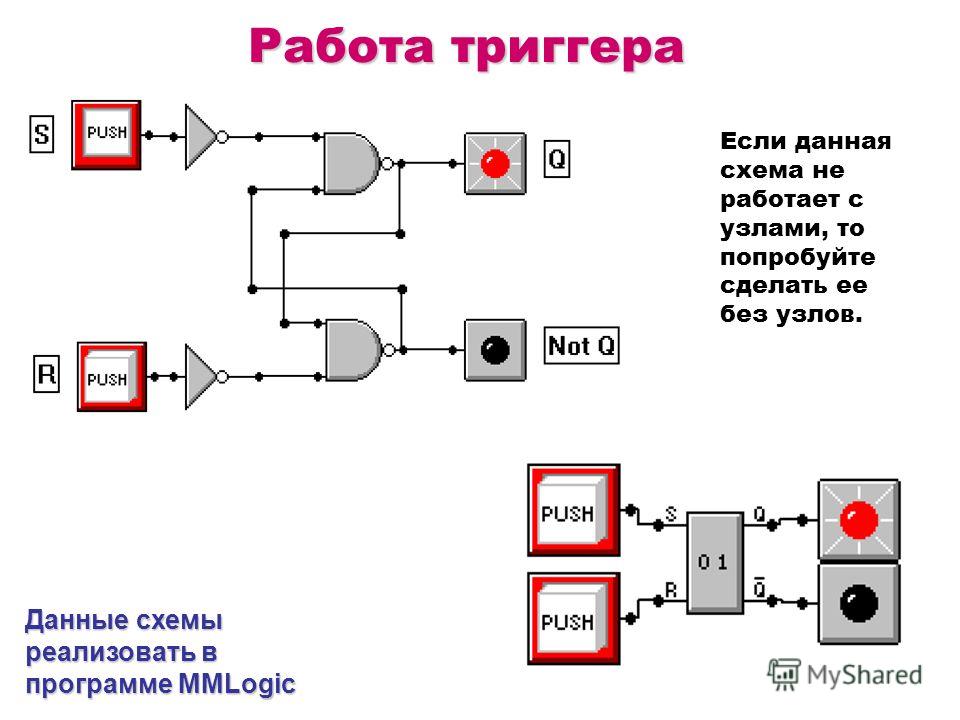
Работа триггера Данные схемы реализовать в программе MMLogic Если данная схема не работает с узлами, то попробуйте сделать ее без узлов.

4

Работа с текстом. Данные схемы реализовать в программе MMLogic Для того, чтобы работал селектор с текстовым файлом, необходимо: а) набрать текст (желательно 16 строк 0-15) и его сохранить; б) установить текстовое окно, ПКМ – Properties: Multiple и связь с файлом (Browse…) в) установить соответствующую связь, при щелчке мышкой по селектору будет отображаться строка, показывающая стрелкой.

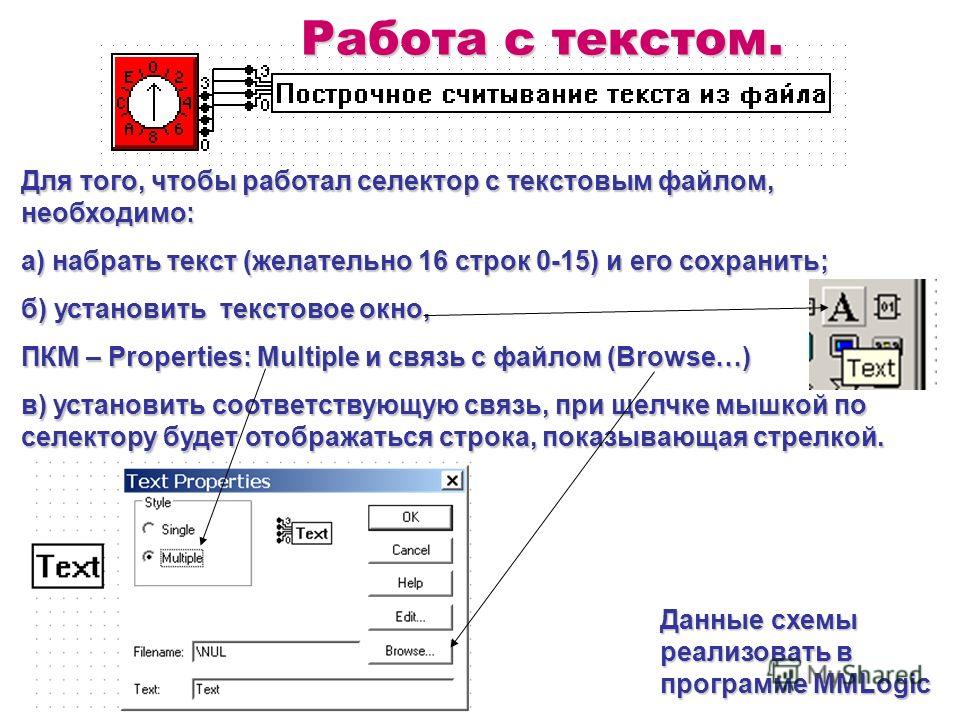
5

АЛУ в действии Данные схемы реализовать в программе MMLogic

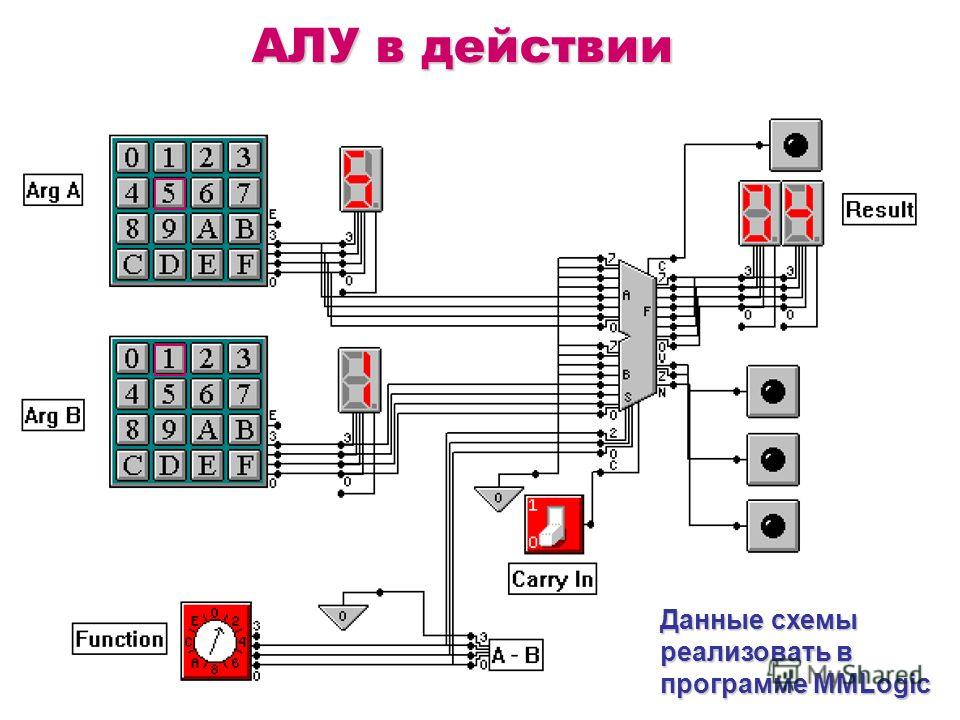
6

Селектор, изображение, клавиатура и дисплей. Данные схемы реализовать в программе MMLogic Рисунки взять на сервере: логика – MMLogic — Pic_Logic и скопировать себе в папку (все от 0 до 15) Настройка элемента изображение на семейство рисунков осуществляется в свойствах (properties), аналогично тексту. Связь установить с рисунком SLOT0

7

Датчик случайных чисел Данные схемы реализовать в программе MMLogic Случайное изображение.

8

1 Логическая схема одноразрядного двоичного сумматора на два входа (полусумматор)

9

ABSP Таблица истинности: Данную схему реализовать в программе MMLogic Логическая схема одноразрядного двоичного сумматора на 2 входа (полуссуматор).

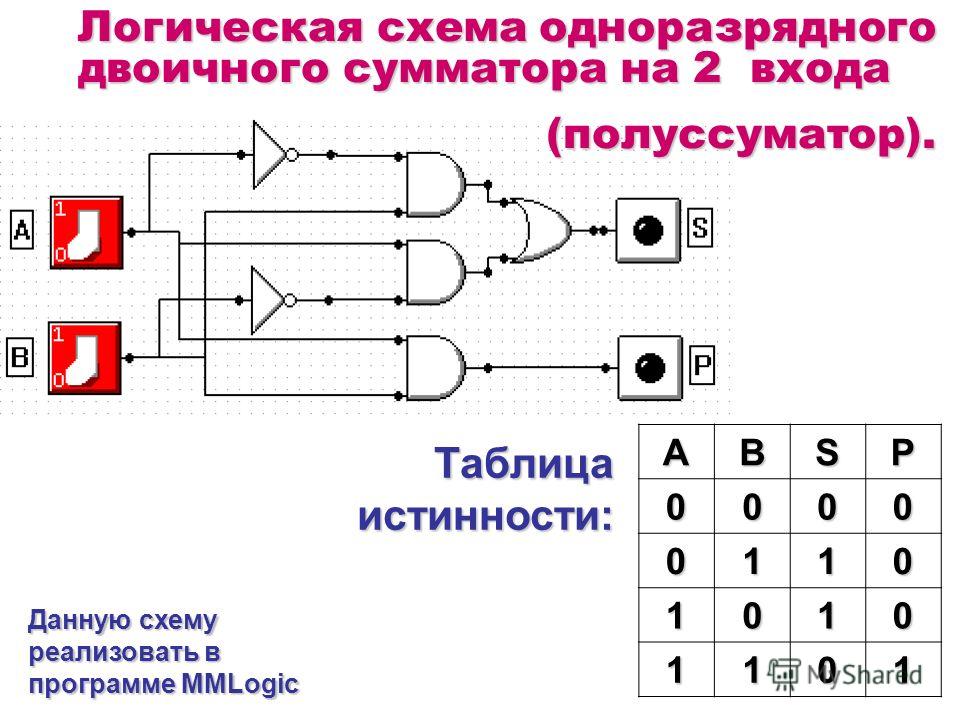
10

Условное обозначение одноразрядного двоичного сумматора на три входа Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах компьютера.

11

Логические схемы одноразрядного двоичного сумматора на 3 входа. с с ABCSP Таблица истинности:

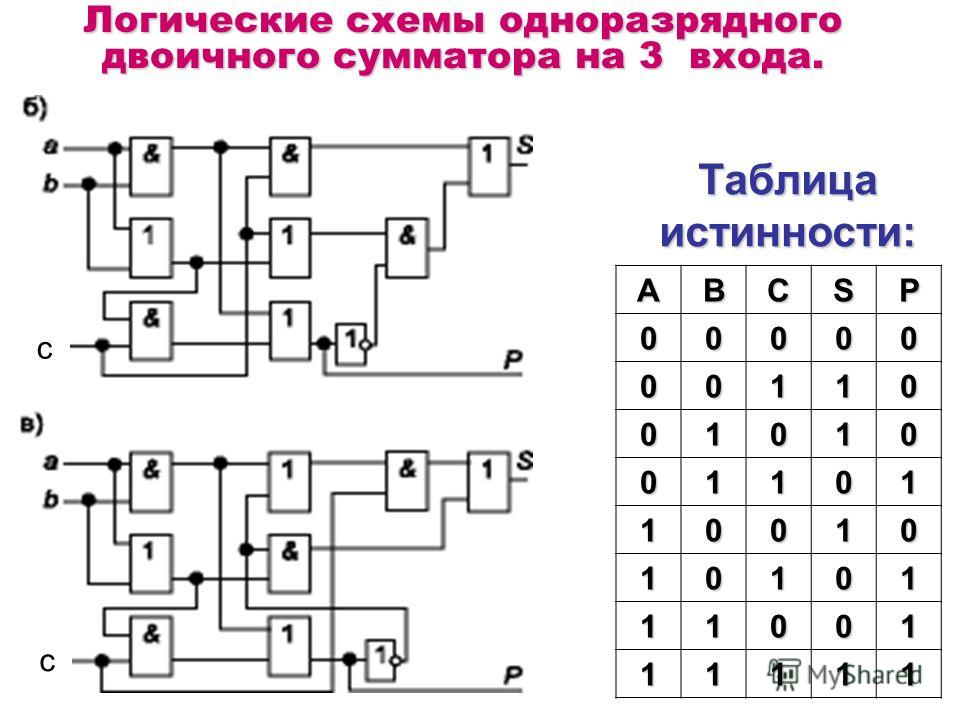
12

Логические схемы одноразрядного двоичного сумматора на 3 входа. Реализация схемы б) в MMLogic схему в) реализовать самостоятельно

13

Сумматор это электронная логическая схема, выполняющая суммирование двоичных чисел Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров. Схема вычисления суммы C = (с 3 c 2 c 1 c 0 ) двух двоичных трехразрядных чисел A = (a 2 a 1 a 0 ) и B = (b 2 b 1 b 0 ) имеет вид:

14

Сумматор двух трехбитных числа: А (а0, а1, а2) и В (b0, b1, b2): первым идет сумматор на 2 входа, все остальные — на 3 входа: a0a0a0a0 b0b0b0b0 s p a1 b1 s p a2 b2sp c0c0c0c0 c1 c2c3 a2a1a0b2b1b0c3c2c1c Таблица истинности: (Рассмотрены не все варианты) Данную схему реализовать в программе MMLogic самостоятельно

15

Действие счетчика на 4 бита. Данные схемы реализовать в программе MMLogic

16

0 разряд 1 разряд 2 разряд Каскад из 3-х счетчиков на 4 бита. Данные схемы реализовать в программе MMLogic

17

Работа 8-ми разрядного элемента памяти Внимание! Данную схему можно не собирать

18

Постоянно меняющееся случайное изображение. Каскад счетчиков служит замедлителем смены рисунка. Данные схемы реализовать в программе MMLogic

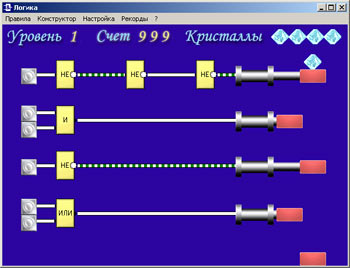
Достоинства

• игровая форма закрепления учебного материала;
• программа имеет встроенный набор логических схем (задач) для каждого из 10 уровней;
• существует возможность составлять новые схемы и проверять их работу, не выходя из программы;
• с каждым уровнем можно связать свою схему; список нестандартных
  схем хранится в файле инициализации LOGIC.INI; таким образом,
  можно составить несколько ini-файлов с разнотипными заданиями;
• кроме стандартного набора логических элементов (И, ИЛИ, НЕ)
  в схемах можно использовать включенные (непонятно почему) в
  школьную программу элементы «импликация», «эквивалентность»,
  а также полусумматор, сумматор и RS-триггер.

5.12. Что такое переключательная схема?

В компьютерах и других автоматических устройствах широко применяются
электрические схемы, содержащие сотни и тысячи переключательных элементов:
реле, выключателей и т.п. Разработка таких схем весьма трудоёмкое дело.
Оказалось, что здесь с успехом может быть использован аппарат алгебры
логики.

Переключательная схема это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал.

Каждый переключатель имеет только два состояния: замкнутое и
разомкнутое.
Переключателю Х поставим в соответствие логическую переменную х,
которая принимает значение 1 в том и только в том случае, когда переключатель
Х замкнут и схема проводит ток; если же переключатель разомкнут, то
х равен нулю.

Будем считать, что два переключателя Х и связаны таким образом, что когда Х замкнут,
то разомкнут, и наоборот.
Следовательно, если переключателю Х поставлена в соответствие логическая
переменная х, то переключателю должна соответствовать переменная .

Всей переключательной схеме также можно поставить в соответствие
логическую переменную, равную единице, если схема проводит ток, и равную
нулю если не проводит. Эта переменная является функцией от
переменных, соответствующих всем переключателям схемы, и называется
функцией проводимости.

Найдем функции проводимости F некоторых переключательных схем:

a)  

Схема не содержит переключателей и проводит ток всегда, следовательно
F=1; 

б)  

Схема содержит один постоянно разомкнутый контакт, следовательно
F=0; 

в)  

Схема проводит ток, когда переключатель х замкнут, и не проводит, когда
х разомкнут, следовательно, F(x) = x; 

г)  

Схема проводит ток, когда переключатель х разомкнут, и не проводит,
когда х замкнут, следовательно, F(x) = ; 

д)  

Схема проводит ток, когда оба переключателя замкнуты, следовательно,
F(x) = x . y; 

е)  

Схема проводит ток, когда хотя бы один из переключателей замкнут,
следовательно, F(x)=x v y; 

ж)  

Схема состоит из двух параллельных ветвей и описывается функцией
. 

Две схемы называются равносильными, если через одну из них проходит ток тогда и только тогда, когда он проходит через другую (при одном и том же входном сигнале). Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей.

Задача нахождения среди равносильных схем наиболее простых является очень
важной. Большой вклад в ее решение внесли российские учёные Ю.И

Журавлев,
С.В. Яблонский и др.

При рассмотрении переключательных схем возникают две основные задачи:
синтез и анализ схемы.

СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим
трём этапам:

1. составлению функции проводимости по таблице истинности, отражающей эти
   условия;
2. упрощению этой функции;
3. построению соответствующей схемы.

АНАЛИЗ СХЕМЫ сводится к

1. определению значений её функции проводимости при всех возможных
   наборах входящих в эту функцию переменных.
2. получению упрощённой формулы.

Примеры.

1. Построим схему, содержащую 4
переключателя x, y, z и t, такую, чтобы она проводила ток тогда и только
тогда, когда замкнут контакт переключателя t и какой-нибудь из остальных
трёх контактов.

Решение. В этом случае можно обойтись без построения таблицы
истинности. Очевидно, что функция проводимости имеет вид
F(x, y, z, t) = t . (x v y v z), а схема
выглядит так:

2. Построим схему с пятью
переключателями, которая проводит ток в том и только в том случае, когда
замкнуты ровно четыре из этих переключателей.

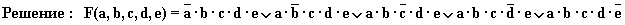
Схема имеет вид:

3. Найдем функцию проводимости схемы:

Решение. Имеется четыре возможных пути прохождения тока при
замкнутых переключателях a, b, c, d, e : через переключатели a, b; через
переключатели a, e, d; через переключатели c, d и через переключатели
c, e, b. Функция проводимости F(a, b, c, d, e) =
a . b   v   a . e . d   v  
c . d   v   c . e . b.

4. Упростим переключательные схемы:

а)  

Решение:   

Упрощенная схема:

б)  

.

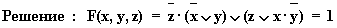Здесь первое логическое слагаемое является отрицанием второго логического слагаемого
, а дизъюнкция
переменной с ее инверсией равна 1.

Упрощенная схема :

в)  

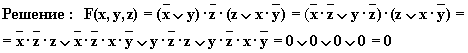
Упрощенная схема:

г)  

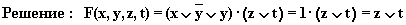
Упрощенная схема:

д)  

(по закону склеивания)

Упрощенная схема:

е)  

Решение: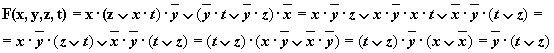

Упрощенная схема:

Аксиомы и законы

Построение таблиц в удобной форме позволяет определить, когда определённое действие или высказывание принимает верное значение, а в каком случае нет. В верхней строчке записывают логическую форму высказывания, а в столбцах – истинные значения. Некоторые комбинации высказываний всегда будут истинными или ложными, независимо от содержания. Поэтому и были сформулированы следующие законы:

1. Торжества. Записывается в виде утверждения: А = А. В этом случае таблица будет состоять из двух комбинаций: ложной и правдивой. Бинарная логическая связка «Если А, то А» является материальной импликацией. Для такого варианта всегда можно сказать, что А есть А. Этот закон обозначает то, что нельзя подменять одно понятие другим, иначе возникнут логические ошибки.
2. Противоречия. Согласно ему, утверждение, что А и НЕ-А, неверно: A {amp}amp; A = 0. Другими словами, если А истинное значение, то его отрицание не может быть ложным. То есть их перемножение будет всегда фальшивой операцией. Этот закон довольно часто применяется для упрощения сложных логических суждений.
3. Третьего исключённого. Закон записывается в виде A v A = 1 и обозначает, что в один и тот же момент высказывание может быть только правдивым или ложным. То есть третьего не дано.

Эти три закона фундаментальны. Без их соблюдения сделать любое правильное утверждение невозможно.

Для решения логических задач с помощью таблиц истинности используют различные формулы, соответствующие разного вида операциям. Одно из них логическое умножение (конъюнкция). В этом случае считается, что функция истинная лишь тогда, когда оба выражения являются верными: F = A {amp}amp; B. Другое логическое сложение (дизъюнкция). Оно гласит, что если оба выражения ложны, то и логическая функция будет неверной.

Кроме того, используется закон:

• инверсии (отрицания) — если логическое высказывание истинно, то отрицание его будет ложным выражением;
• импликации (следования) — для всегда истинного сложного логического выражения ложь будет тогда, когда из верности следует отрицание;
• эквивалентности (равнозначности) — выражение будет истинным лишь тогда, когда оба высказывания имеют одинаковое значение.

Материалы по MMLogic

К сожалению, материалов по MMLogic на русском языке очень мало:

• Каждая страница разделена на секции, каждая секция описывается названием (навигация по заголовкам).
• Наиболее важным разделам присвоена определенная роль (навигация по ориентирам)
• В верхней части каждой страницы вы найдете меню быстрого перехода ( ссылки внутренней навигации). Каждая ссылка привязана к определенной клавише (кнопке быстрого вызова).

Внимание: вы используете устаревший браузер! Мы советуем вам обновить программное обеспечение до новой версии или скачать альтернативный браузер: здесь вы можете загрузить последнюю версию Firefox.Если вы работаете в операционной системе Windows на компьютере с низкой производительностью Midori. Внимание, ваш браузер устарел и больше не поддерживается

Мы рекомендуем просматривать наш вебсайт в режиме полный доступ

Внимание, ваш браузер устарел и больше не поддерживается. Мы рекомендуем просматривать наш вебсайт в режиме полный доступ

Что это такое?

Multimedia Logic (MMLogic) — это бесплатная программа-конструктор, с помощью которой можно моделировать логические схемы любой сложности и устройства компьютера. Её автор — George Mills — разместил на сайте фирмы Softronix не только исполняемый файл программы, но и её исходные тексты на Visual C++ 7.1.

В оригинальной версии MMLogic существует две проблемы:

1. интерфейс программы — англоязычный;
2. в программе используются зарубежные обозначения логических элементов, которые сильно отличаются от отечественных (ГОСТ 2.743—91).

Эти проблемы существенно сдерживали внедрение программы MMLogic в учебный процесс в российских школах. На этой странице представлена русскоязычная версия программы, в которой используются обозначения логических элементов согласно ГОСТ 2.743—91.

Спасибо В.И. Глезденеву (МБОУ Лицей № 8, г

Сосновый Бор), который привлёк внимание автора к этой программе

Установка программы

Порядок установки русифицированной версии (исполняемый файл и справочная система):

1. скачать и установить оригинальную версию программы
   с официального сайта (www.softronix.com).
2. скачать (с этого сайта) один из двух вариантов русификации:
   • MMLogic_rus1 — с зарубежными обозначениям логических элементов;
     (архив RAR, 398 Кб; пароль — kpolyakov.spb.ru)
   • MMLogic_rus2 — с обозначениями по ГОСТ 2.743—91 (архив RAR, 389 Кб;
     пароль — kpolyakov.spb.ru)
3. скопировать русифицированный файл (MMLogic_rus1.exe или MMLogic_rus2.exe)
   в папку программы (по умолчанию — %Program Files%\Softronix\Multimedia Logic) и запускать его
   вместо оригинального файла MMLogic.exe.
4. поместить в ту же папку (рядом с исполняемым файлом) два файла
   русифицированной справочной системы (MMLogic_rus*.hlp и MMLogic_rus*.cnt).

Установка программы

Порядок установки русифицированной версии (исполняемый файл и справочная система):

1. скачать и установить оригинальную версию программы с официального сайта (www.softronix.com).
2. скачать (с этого сайта) один из двух вариантов русификации:
3. MMLogic_rus1 — с зарубежными обозначениям логических элементов; (архив RAR, 398 Кб; пароль — kpolyakov.spb.ru)
4. MMLogic_rus2 — с обозначениями по ГОСТ 2.743—91 (архив RAR, 389 Кб; пароль — kpolyakov.spb.ru)
5. скопировать русифицированный файл (MMLogic_rus1.exe или MMLogic_rus2.exe) в папку программы (по умолчанию — %Program Files%SoftronixMultimedia Logic) и запускать его вместо оригинального файла MMLogic.exe.
6. поместить в ту же папку (рядом с исполняемым файлом) два файла русифицированной справочной системы (MMLogic_rus*.hlp и MMLogic_rus*.cnt).

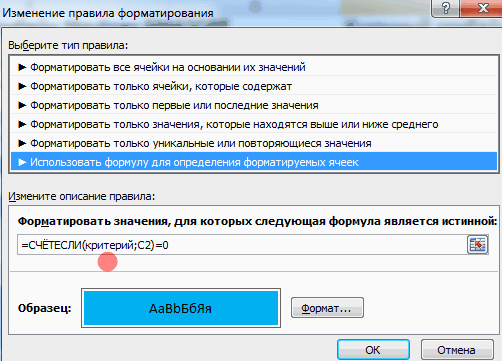
Пример задания

Пусть необходимо построить таблицу для логического выражения F = (A → B) * (A B). Эта формула состоит из двух логических переменных A и B и нескольких операций. Начинают построение с определения строк. Используя формулу 2n 1 для рассматриваемого примера можно установить, что их число будет: x = 22 1 = 5.

Теперь следует определить число столбцов. Для этого используется формула, в которой учитывается количество переменных и операций. Последние можно просто посчитать, сложив количество разных знаков, используемых в записи формулы. Но правильней сначала расставить порядок операций, а затем посчитать. Согласно порядку действия над операциями их нумерацию можно представить в следующей очерёдности:

1. Импликация в первой скобке.
2. Инверсия во второй скобке переменной A.
3. Отрицание во второй скобке неизвестной B.
4. Сложение во втором члене.
5. Конъюнкция.

Для этого нужно использовать законы. Необходимо выполнить логическое умножение значений в скобках. Первой и второй строчке будет соответствовать операция произведения один на один, что в ответе даст единицу. Третьей и четвёртой – ноль на один, что в итоге даст ноль. Последний столбец является главным для рассматриваемой логической функции. По нему можно узнать значение логической функции для любых форм переменных A и B.

Это довольно простая задача, содержащая всего две переменных. Но в реальности, например, в программировании, их может быть намного больше. Решать такие задания методом перебора проблематично. Поэтому при решении сложных примеров функцию вначале пытаются упростить.

Например, заданно выражение (x y z) * (x y). По сути, оно записано в совершенно нормальной конъюнктивной форме. Но для приведения его к этому виду нужно, чтобы во втором выражении стояла z

Для того чтобы её добавить необходимо обратить внимание на то, что внутри скобок стоит логическое сложение

Определяем выигрышную покерную руку с помощью map/reduce на JavaScript

Перевод

Вы, как и я, может, иногда участвуете в мини-соревнованиях по олимпиадному программированию. Обычно на то, чтобы придумать решение, в котором более одной-двух строк с использованием какой-то нестандартной функции, у меня нет времени, но в этот раз задача была в том, чтобы определять старшие (выигрышные) покерные руки, и мне показалось что это из тех задач, которая «должна» быть лёгкой!
Получившийся у меня результат корректен, лаконичен и читабелен (по крайней мере, гораздо короче, чем решения, предложенные другими участниками).
Конечно же, в данном случае можно воспользоваться map и reduce, чтобы получить необходимую информацию. Вышел действительно удачный пример того, как использовать эти инструменты для решения в несколько шагов практических задач.