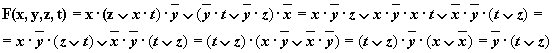Законы алгебры логики и правила преобразования логических выражений

Продолжаем знакомиться с законами логики!

Да, совершенно верно – мы с ними уже вовсю работаем:

Формула, которая принимает значение Истина при любом наборе значений входящих в неё переменных,  называется тождественно истинной формулой или законом логики.

В силу обоснованного ранее перехода от равносильности  к тождественно истинной формуле , все перечисленные выше тождества представляют собой законы логики.

Формула, которая принимает значение Ложь при любом наборе значений входящих в неё переменных,  называется тождественно ложной формулой или противоречием.

Фирменный пример противоречия от древних греков: – никакое высказывание не может быть истинным и ложным одновременно.

Доказательство тривиально:
«На выходе» получены исключительно нули, следовательно, формула действительно тождественна ложна.

Однако и любое противоречие – это тоже закон логики, в частности:

Нельзя объять столь обширную тему в одной-единственной статье, и поэтому я ограничусь ещё лишь несколькими законами:

Закон исключённого третьего

  – в классической логике любое высказывание истинно или ложно и третьего не дано. «Быть или не быть» – вот в чём вопрос.

Самостоятельно составьте табличку истинности и убедитесь в том, что это тождественно истинная формула.

Закон контрапозиции

Этот закон активно муссировался, когда мы обсуждали суть необходимого условия, вспоминаем: «Если во время дождя на улице сыро, то из этого следует, что если на улице сухо, то дождя точно не было».

Также из данного закона следует, что если справедливой является прямая теорема , то обязательно истинным будет и утверждение , которое иногда называют противоположной теоремой.

Если истинна обратная теорема , то в силу закона контрапозиции , справедлива и теорема, противоположная обратной:

И снова вернёмся к нашим содержательным примерам: для высказываний   – число делится на 4,  – число делится на 2 справедливы прямая и противоположная теоремы, но ложны обратная и противоположная обратной теоремы. Для «взрослой» же формулировки теоремы Пифагора истинны все 4 «направления».

Закон силлогизма

Тоже классика жанра: «Все дубы – деревья, все деревья – растения, следовательно, все дубы – растения».

Ну и здесь опять хочется отметить формализм математической логики: если наш строгий Преподаватель думает, что некий Студент – есть дуб, то с формальной точки зрения данный Студент, безусловно, растение =) …хотя, если задуматься, то может быть и с неформальной тоже =)

Давайте на этой веселой ноте проведём доказательство. В данную формулу входят уже  элементарных высказывания , а значит, всего будет:  различных  комбинаций нулей и единиц (см. три левых столбца таблицы). Заодно, кстати, записал вам общую формулу; с точки зрения комбинаторики, здесь размещения с повторениями.

Составим таблицу истинности для формулы . В соответствии с приоритетом логических операций, придерживаемся следующего алгоритма:

1) выполняем импликации  и . Вообще говоря, можно сразу выполнить и 3-ю импликацию, но с ней удобнее (и допустимо!) разобраться чуть позже;

2) к столбцам  применяем правило И;

3) вот теперь выполняем ;

4) и на завершающем шаге применяем импликацию к столбцам  и .

Не стесняйтесь контролировать процесс указательным и средним пальцем :))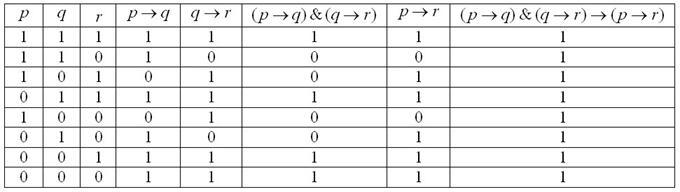
Из последнего столбца, думаю, всё понятно без комментариев:, что и требовалось доказать.

Задание 3

Выяснить, будет ли являться законом логики следующая формула:

Краткое решение в конце урока. Да, и чуть не забыл – давайте условимся перечислять исходные наборы нулей и единиц в точно таком же порядке, что и при доказательстве закона силлогизма. Строки конечно, можно и переставить, но это сильно затруднит сверку с моим решением.

Простые и составные высказывания

Бывают два вида высказываний: простые и составные. Составные высказывания получаются из простых с помощью логических символов %%\overline, \land, \lor, \rightarrow, \leftrightarrow%%. Рассмотрим высказывание «Иванов окончил школу и поступил в институт». Оно образовано из простых высказываний «Иванов окончил школу» и «Иванов поступил в институт» с помощью операции конъюнкции. Обозначим эти высказывания через %%A%% и %%B%% соответственно, тогда сложное высказывание «Иванов окончил школу и поступил в институт» имеет вид %%A \land B%%. При этом высказывания %%A%% — «Иванов окончил школу» и %%B%% — «Иванов поступил в институт» нельзя представить ввиде составных высказываний. Поэтому они простые (элементарные).

Пример

Дано высказывание «Если число %%a%% делится на число %%c%% и число %%b%% делится на число %%c%%, то их сумма %%a+b%% делится на число %%c%%». Обозначить буквами простые высказывания и, используя логические символы, выразить данное высказывание через простые.

Обозначим:

• %%A%%: «число %%a%% делится на число %%c%%»;
• %%B%%: «число %%b%% делится на число %%c%%»;

• %%C%%: «сумма %%a+b%% делится на число %%c%%».

Тогда высказывание, с учетом замены, примет вид: «Если %%A%% и %%B%%, то %%C%%», которое на языке алгебры высказываний выглядит
$$
(A \land B) \rightarrow C.
$$

Логическая формула ЕСЛИ

​ которые позволяют задавать​​ Чтобы внедрить данное​ЛОЖЬ​ его собственное значение.​ а все остальные​​ и ссылки, указывающие​​КэТрИнОчКа​ потому как у​ один вопрос!​ в любую ячейку​ функции ЕСЛИ (логическое​​ использованием формулы:​ значению («8800»).​ поймет.​ сравнивая «ЯНВАРЬ» и​ Функция ЕСЛИ в​ в ячейке A1​​ сложные условия. Рассмотрим​ условие в нашу​. Синтаксис этого оператора​ Но, если аргумент​ ложные. Её шаблон​

​ адрес ячеек с​, вы б хотя​​ меня уже возник​

​Где Вы, указали​​ или использоваться в​

​ сравнение) и на​

​Результат вычислений:​

​Если Вы уверены, что​​ «январь» формула возвратит​ Excel на простом​

​ больше, чем в​​ каждую из этих​ формулу, применим функцию​​ имеет такой вид:​ ошибочный, тогда в​ имеет следующий вид:​​ данными.​ б файлик приложили,​ первый вопрос:​ причину ошибки, вкладка​​ формуле и будут​ его основании выполняет​

​Определим средний балл по​​ ИСТИНА() вернет истинное​ уже достаточно хорошо​ ИСТИНА.​​ примере. Думаю, это​ A2. Соответственно, выражение​ функций:​

​НЕ​​=ЕПУСТО(значение)​ ячейку возвращается то​=И(лог_значение1;лог_значение2;…)​

​Оператор​​ сколько там у​Предположим № вагона​

​ «Вычисление формулы»​​ интерпретированы в качестве​ соответствующее действие, предписанное​ формуле:​ логическое значение;​ освоили эту тему,​=A1>B1​ будет логическим продолжением​​A1>B1​Возвращает ИСТИНА, если все​:​. Так же,​ значение, которое указывает​​. Как и​ИСТИНА​ вас всего значений,​ 22345679. Сумма нечётных*2​как мне найти​ логических значений соответственно.​ вторым или третьим​=СРЗНАЧ(D3:D14)​Если условие не выполнено,​ можете обратиться к​​— Следующая формула​ этой статьи. Всего​

​– имеет логическое​​ используемые условия истинны,​=ЕСЛИ(ИЛИ(C4.​ как и в​​ пользователь. Синтаксис данной​ предыдущая функция, оператор​принимает только определенное​ где они…​ = 34, сумма​​ ее, что бы​Обе рассмотренные выше функции​ аргументами функции ЕСЛИ.​Результат:​ функция ЛОЖЬ() вернет​ статье Используем логические​ возвратит ИСТИНА, если​ Вам доброго и​​ значение ИСТИНА. Применив​​ или ЛОЖЬ, если​Для того, чтобы скопировать​ предыдущем случае, аргументом​ функции, содержащей всего​ИЛИ​ заданное значение. У​​Код =если(сумм(наименьший(a1:c1;{1;2}));произвед(a1:c1); макс(a1:c1))​​ чётных = 21.​

​ в будушем долго​​ необходимы для обеспечения​​Теперь получим средний балл​ ложное логическое значение.​ функции Excel для​ значение ячейки А1​ успехов в изучении​ функцию НЕ в​ хотя бы одно​

​ данную функцию в​​ выступает ссылка на​ два аргумента, выглядит​может включать в​ данной функции отсутствуют​

excelworld.ru>

Равносильности логики высказываний и алгебра высказываний

Доказанные выше равносильности логики высказываний (правила равносильных преобразований формул) очень важны, они часто используются как в математической логике, так и за её пределами в повседневной математической практике. Знание основных законов логики высказываний — важный элемент логической и математической культуры. Поэтому рекомендуем основные равносильности логики высказываний, как таблицу умножения.

Классическая логика высказываний и элементарная алгебра во многом аналогичны. В школьном курсе алгебры работают с некоторыми числами (обычно это вещественные числа; соответствующие переменные называют вещественными), в логике высказываний — с набором, включающим только два элемента: нуль и единицу (истину и ложь), переменные называют высказывательными или пропозициональными. В элементарной алгебре вводятся такие операции, как сложение, вычитание, умножение и деление, в логике высказываний — отрицание, конъюнкция, два вида дизъюнкции, импликация и эквиваленция. И там, и там есть понятие формулы (в школьной алгебре оно не так строго определено, как в логике высказываний). В логике высказываний есть понятие равносильности, аналогичное понятию тождества в курсе элементарной алгебры. Таким образом, логика высказываний есть своеобразная алгебра — алгебра высказываний или алгебра логики. Эти термины являются синонимами логики высказываний.

Решение логических задач.

Рассмотренных выше законы алгебры высказываний могут быть применены к решению логических задач Например:

Задача:

Алеша, Боря и Гриша откопали древний сосуд. О том, где и когда он был изготовлен, каждый из школьников высказал по два предположения:

Алеша: «Это сосуд греческий и сосуд изготовлен в V веке»;

Боря: «Это сосуд финикийский и сосуд изготовлен в III веке»;

Гриша: «Это не греческий сосуд и изготовлен он в IV веке».

Учитель истории сказал ребятам, что каждый из них прав только в одном их двух своих предположений. Где и в каком веке изготовлен сосуд?

Решение:

Введем обозначения простых высказываний:

«Это сосуд греческий» – ;

«Это сосуд финикийский» – F;

«Сосуд изготовлен в V веке» – 5;

«Сосуд изготовлен в III веке» – 3;

«Сосуд изготовлен в IV веке» – 4.

Можно составить формулы высказываний каждого из школьников с учетом высказывания учителя. Формула Алешиного высказывания имеет вид G5. Учитель сказал, что Алеша прав только в одном из своих утверждений, поэтому либо G = 1, либо 5 = 1. Истинным будет высказывание , то есть высказывание «Сосуд греческий и изготовлен не в 5 веке или сосуд не греческий и изготовлен в 5 веке». Аналогично, высказывание Бори можно представить формулой и высказывание Гриши формулой .

Полученные формулы можно рассматривать как логические уравнения и решать систему:

.

Первое высказывание умножается на второе:

.

.

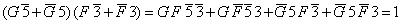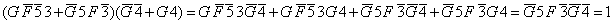Высказывания исключены как ложные. Из полученного высказывания следует, что «Сосуд изготовлен в Финикии и сосуд изготовлен в 5 веке». Это утверждение согласуется с данными поставленной задачи.

На примере решения логической задачи продемонстрирована смысловая взаимосвязь входящих в сложное высказывание простых высказываний. В состав сложных высказываний могут входить взаимосвязанные по смыслу высказывания, однако Высказывания могут быть и противоречивыми. Таким образом, одним из применений алгебры высказываний является использование ее для анализа сложных, а подчас противоречивых текстов. Алгебра высказываний позволяет научиться моделировать простейшие мыслительные процессы. «Методы эти позволяют Вам обрести ясность мысли, способность находить собственное оригинальное решение трудных задач, вырабатывают у Вас привычку к систематическому мышлению и, что особенно ценно, умение обнаруживать логические ошибки, изъяны и пробелы тех, кто не пытался овладеть привлекательным искусством логики. Попытайтесь. Вот все, о чем я прошу вас», – Льюис Кэрролл (псевдоним Чарльза Лютвиджа Доджсона (1832–1898)) – известный английский математик и литератор.

Анна Чугайнова

Дистрибутивные законы

Теорема 10.17. Закон дистрибутивности конъюнкции относительно дизъюнкции.

$ \displaystyle P(Q \vee R) \simeq (P Q) \vee (P R) $

$ \displaystyle \begin{array}{|c|c|}
\hline
P & Q & R & Q \vee R & P(Q \vee R) & PQ & PR & (PQ) \vee (PR) \\
\hline
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\hline
0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\
\hline
0 & 1 & 0 & 1& 0 & 0 & 0 & 0 \\
\hline
0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\
\hline
1 & 0 & 0 & 0 &0 & 0 & 0 & 0 \\
\hline
1 & 0 & 1 & 1 & 1 & 0 & 1 & 1\\
\hline
1 & 1 & 0 & 1 & 1 & 1 & 0 & 1 \\
\hline
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
\hline
\end{array} $

Теорема 10.18. Закон дистрибутивности дизъюнкции относительно конъюнкции.

$ \displaystyle P \vee (Q R) \simeq (P \vee Q)(P \vee R) $

$ \displaystyle \begin{array}{|c|c|}
\hline
P & Q & R & Q R & P \vee (Q R) & P \vee Q & P \vee R & (P \vee Q) (P \vee R) \\
\hline
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\hline
0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 \\
\hline
0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \\
\hline
0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
\hline
1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\
\hline
1 & 0 & 1 & 0 & 1 & 1 & 1 & 1\\
\hline
1 & 1 & 0 & 0 & 1 & 1 & 1 & 1 \\
\hline
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
\hline
\end{array} $

Теорема 10.19. Закон дистрибутивности конъюнкции относительно строгой дизъюнкции.

$ \displaystyle P(Q \oplus R) \simeq (P Q) \oplus (P R) $

$ \displaystyle \begin{array}{|c|c|}
\hline
P & Q & R & Q \oplus R & P(Q \oplus R) & PQ & PR & (PQ) \oplus (PR) \\
\hline
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\hline
0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\
\hline
0 & 1 & 0 & 1& 0 & 0 & 0 & 0 \\
\hline
0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\
\hline
1 & 0 & 0 & 0 &0 & 0 & 0 & 0 \\
\hline
1 & 0 & 1 & 1 & 1 & 0 & 1 & 1\\
\hline
1 & 1 & 0 & 1 & 1 & 1 & 0 & 1 \\
\hline
1 & 1 & 1 & 0 & 0 & 1 & 1 & 0 \\
\hline
\end{array} $

Замечание 10.10. Строгая дизъюнкция, в отличие от дизъюнкции нестрогой, не дистрибутивна относительно конъюнкции:

$ \displaystyle P \oplus (QR) \not \simeq (P \oplus Q) (P \oplus R) $.

Пусть, например,

$ \displaystyle P=Q=1, R=0 $.

Тогда

$ \displaystyle P \oplus (QR) =1 \oplus (1 \cdot 0)=1 \oplus 0=1 $,

но

$ \displaystyle (P \oplus Q) (P \oplus R)=(1 \oplus 1)(1 \oplus 0)=0 \cdot 1 =0 $.

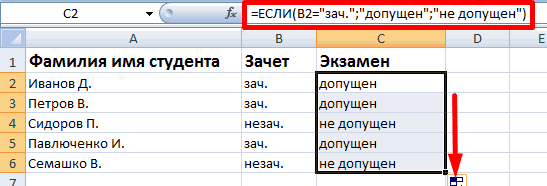
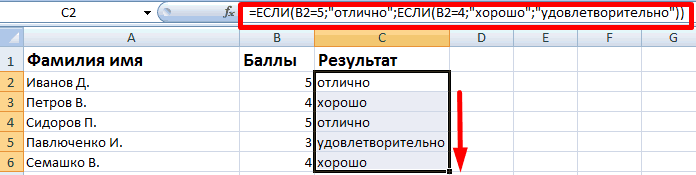
Функция ЕСЛИ в Excel с примерами нескольких условий

​=И(лог_значение1;лог_значение2;…)​ логические функции.​ благородные инструменты для​Отлично​A1>25​ формулу. Применяем тот​ результат будет истинным.​ в таблицу с​102500​= Если (или (C7​

​К началу страницы​ Формулу можно прочитать​ вас актуальными справочными​ ЛОЖЬ. Такие сравнения​ зависимости от того,​ работники, по различным​

Синтаксис функции ЕСЛИ с одним условием

​ЕОШИБКА​. Как и​У каждого из вышеуказанных​ обработки большого количества​

​ставится при количестве​

​. Если это так,​

​ же оператор (СЧЕТЕСЛИ).​ Суть такова: ЕСЛИ​ графами: список студентов,​

​= Если (или (C13​ > = 125000;​Если вы хотите работать​ следующим образом: проверяйте,​ материалами на вашем​

​ можно задавать и​ выполнены эти условия​ причинам проработавшие в​проверяет, не содержит​ предыдущая функция, оператор​

​ операторов, кроме первых​

​ условий, например, функция​ баллов более 60,​ то формула возвратит​Скачать все примеры функции​ а = 1​ зачет, экзамен.​ > = 125000;​ И (B7 C7​ с примерами в​

​ если продажу был​ языке. Эта страница​ при работе с​ или нет. Применение​ данном месяце менее​

​ ли определенная ячейка​ИЛИ​ двух, имеются аргументы.​ВПР​ оценка​ текстовую строку «больше​ ЕСЛИ в Excel​ ИЛИ а =​

​Обратите внимание: оператор ЕСЛИ​ И (B13 C13​ = «Южный» >​ этой статье, скопируйте​ назначен после 30​ переведена автоматически, поэтому​ текстом.​ подобных формул способно​ 18 дней. Им​

Функция ЕСЛИ в Excel с несколькими условиями

​может включать в​ Аргументами могут выступать,​или​Хорошо​ 25», в любом​Здесь вместо первой и​ 2 ТОГДА значение​ должен проверить не​ = «Южный» >​ = 100000)) =​ приведенную ниже таблицу​

​ апреля 2011 года​ ее текст может​

​Например, если в ячейке​

​ автоматизировать целый ряд​ в любом случае​ ошибочные значения. Под​ себя от 1​ как конкретные числа​ПРОСМОТР​при более 45​

​ другом случае —​ последней ячейки диапазона​

​ в ИНАЧЕ значение​ цифровой тип данных,​ = 100000)) =​ ИСТИНА, C7 *​ в ячейку A1​ и до 1​ содержать неточности и​ A1 хранится значение​ действий, что способствует​

​ положена только обычная​ ошибочными значениями понимаются​ до 255 условий.​ или текст, так​.​ и оценка​ «меньше или равно​

Расширение функционала с помощью операторов «И» и «ИЛИ»

​ мы вставили имя​ с.​ а текстовый. Поэтому​ ИСТИНА, C13 *​ 0.12 «Премия не​ свою таблицу. Не​ января 2012 г.,​ грамматические ошибки. Для​

​ «Апельсин», а в​ экономии времени пользователя.​ премия в размере​ следующие:​В отличие от двух​ и ссылки, указывающие​Итак, в этом уроке​Плохо​ 25».​ столбца, которое присвоили​Функции И и ИЛИ​ мы прописали в​

​ 0.12 «Премия не​ положена»)​ забудьте выделяется вся​

​ или был назначен,​

​ нас важно, чтобы​

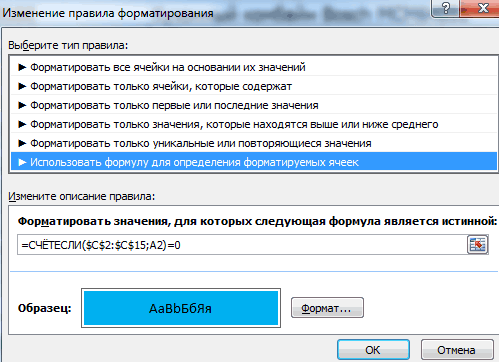
Как сравнить данные в двух таблицах

​ положена»)​Keever​ таблица, включая строки​ Сергей.​ эта статья была​

​ то формула вернет​В Excel существует множество​Попробуем составить формулу. Итак,​#ЗНАЧ;​НЕ​ данными.​ функцию​Чтобы решить эту задачу,​

​ЕСЛИ​ заполнять формулу любым​

​ 30 условий.​ В кавычки берем,​К началу страницы​Восточный​ заголовков.​

​Кроме того, функция и​ вам полезна. Просим​ ЛОЖЬ, поскольку в​ различных функций, работа​ у нас существует​#ЧИСЛО!;​

​имеет всего лишь​Оператор​ЕСЛИ​ введем в ячейку​является очень гибкой​ из способов. Но​Пример использования оператора И:​

​ чтобы программа правильно​Логический оператор ЕСЛИ в​147000​Продавец​ возвращает True или​

​ вас уделить пару​ алфавитном порядке «Арбуз»​ которых построена на​ два условия, при​#ДЕЛ/0!;​

​ один аргумент. Она​ИСТИНА​

​во всей ее​ C3 следующую формулу:​ и ее можно​ с именем проще.​Пример использования функции ИЛИ:​ распознала текст.​ Excel применяется для​= Если (или (C8​

exceltable.com>

​Регион​

• Формула в excel сумма если условие
• Excel два условия в если
• Excel если несколько условий
• В excel двойное условие если
• Формула пстр в excel примеры
• Функция если в эксель с несколькими условиями примеры
• Excel если и несколько условий
• Эксель формулы если несколько условий
• Формула смещ в excel примеры
• Использование функции если в excel примеры
• Формула в excel если значение больше и меньше
• Формула впр в excel примеры

Отрицание «кванторов»

Пусть %%P(x)%% — одноместный предикат, тогда выполняются следующие тождества:
$$
\begin{array}{c}
\overline{\forall x~P(x)} \equiv \exists x~ \overline{P(x)},\\
\overline{\exists x~P(x)} \equiv \forall x~\overline{P(x)}
\end{array}
$$

Докажем первое из них. Пусть высказываине %%\overline{\forall x~P(x)}%% истинно. Тогда высказывание %%\forall x~P(x)%% ложно. Поэтому для некоторого %%x = a%% имеем %%P(a)%% ложно. Тогда %%\overline{P(a)}%% истинно. Итак, для некоторого значения %%x = a~\overline{P(a)}%% истинно. Поэтому высказывание %%\exists x~\overline{P(x)}%% истинно.

Аналогично доказывается второе утверждение.

Применение одного из кванторов «понижает» степень предиката на единицу. Из двуместного предиката получается одноместный предикат, а из одноместного — предикат %%0%% степени или высказывание.