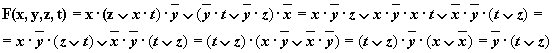Математическая логика, преобразования

1.4. Законы алгебры логики

На основе рассмотренных выше аксиом, выводятся теоремы,
содержащие основные законы АЛ:

1. Закон нулевого множества:
2. Закон универсального множества:
3. Закон повторения:
4. Закон двойной инверсии:
5. Законы дополнительности:

   а) исключенного третьего

   б) логическое противоречие

6. Коммутативный (переместительный) закон:
7. Ассоциативный (сочетательный) закон:
8. Дистрибутивный (распределительный) закон:
9. Законы поглощения:
10. Законы склеивания:

    а) полного

    б) неполного

11. Законы инверсии (теоремы де Моргана):
12. Теоремы разложения (декомпозиции ЛФ):

    f (x,y,…,z) =
    x& f (1,y,…,z) v
    x& f (0,y,…,z);   (1.16a)

    f (x,y,…,z) = (xv f (0,y,…,z))&(xv f
    (1,y,…,z)). (1.16b)

13. Следствия из теорем разложения:
14. Теорема Шеннона (обобщение теорем де Моргана):

Данная теорема утверждает, что инверсия любой функции в АЛ
получается путем замены каждой переменной ее инверсией и
одновременно взаимной заменой символов конъюнкции и дизъюнкции.

Справедливость любого закона АЛ можно доказать разными
методами. доказываются путем прямой подстановки
вместо переменной значений 0 и 1. Ряд законов доказывается
методом перебора всех возможных значений переменных, для которых
проверяется справедливость закона. Для доказательства закона
достаточно показать тождественность выражений, образующих левую
и правую стороны доказываемого соотношения при всех наборах
переменных, принимающих значения 0 или 1. Общий формальный метод
доказательства законов АЛ состоит в том, что справедливость
каждого закона доказывается на основе аксиом и ранее доказанных
законов. Доказательство заключается в приведении обеих частей
выражения к одному виду с помощью последовательных преобразований.
Для доказательства законов инверсии следует воспользоваться
методом математической индукции.

Рассмотрим следующие примеры:

Пример 1.1.
Доказать справедливость закона нулевого множества.

Рассмотрим запись закона в виде 0 v x = x. Проверим
справедливость этого равенства для всех возможных значений x.
При x = 0 получаем равенство 0 v 0 = 0, справедливое по
. При x = 1 имеем 0 v 1 = 1 также в соответствии
с . Таким образом, равенство 0 v x = x
выполняется при всех возможных значениях переменной x,
следовательно является теоремой.

Рассмотрим запись закона в виде 0 & x = 0.
При x = 0 имеем 0 & 0 = 0, в соответствии с .
При x = 1 имеем 0 & 1 = 0 также по ,
следовательно закон выполняется.

Рассмотрим запись закона в виде:

0 & x₁& x₂ … x_n … = 0.

Воспользуемся методом индукции. Первым этапом данного метода
является доказательство истинности теоремы при n = 1. Это положение
уже было доказано нами выше. Теперь предположим, что теорема
справедлива при некотором n и докажем, что она справедлива и при
n+1.

Действительно, при некотором n будем иметь равенство:

0 & x₁& x₂ … x_n = 0.

Для n+1 выражение примет вид:

0 & x₁& x₂ …
x_n& x_n+1 = 0.

Но на основании предположения индукции можно записать
0 & x_n+1 = 0, то есть мы вернулись к
рассмотренному выше случаю одной переменной. Таким образом,
справедливость закона нулевого множества доказана для
произвольного числа переменных.

Пример 1.2.
Доказать справедливость закона поглощения. Будем считать, что
справедливость уже доказана. В
процессе преобразований над знаком равенства будем ставить номер
формулы использованного закона или аксиомы.

Для получим:

x&(xvy) =
x&xvx&y =
xvx&y =
x&1vx&y =
x&(1vy) =
x&1 = x.

Для получим:

xvx&y
=
x&1vx&y =
x&(1vy) =
x&1 = x.

Доказательства остальных законов АЛ читатель может вполне
выполнить самостоятельно, пользуясь аналогичными методами.

Законы логики и правила преобразования логических выражений

1. Закон двойного отрицания (двойное отрицание исключает отрицание):

А = .

2. Переместительный (коммутативный) закон:

— для логического сложения: А Ú B = B Ú A;

— для логического умножения: A & B = B & A.

Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.

3. Сочетательный (ассоциативный) закон:

— для логического сложения: (А Ú B) Ú C = A Ú (B Ú C);

— для логического умножения: (A & B) & C = A & (B & C).

При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

4. Распределительный (дистрибутивный) закон:

— для логического сложения: (А Ú B) & C = (A & C) Ú (B & C);

— для логического умножения: (A & B) Ú C = (A Ú C) & (B Ú C).

Закон определяет правило выноса общего высказывания за скобку.

5. Закон общей инверсии (законы де Моргана):

— для логического сложения: = & ;

— для логического умножения: = Ú

6. Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный):

— для логического сложения: А Ú A = A;

— для логического умножения: A & A = A .

Закон означает отсутствие показателей степени.

7. Законы исключения констант:

— для логического сложения: А Ú 1 = 1, А Ú 0 = A;

— для логического умножения: A & 1 = A, A & 0 = 0.

8. Закон противоречия:

— A & = 0.

Невозможно, чтобы противоречащие высказывания были одновременно истинными.

9. Закон исключения третьего:

— A Ú = 1.

Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.

10. Закон поглощения

— для логического сложения: А Ú (A & B) = A;

— для логического умножения: A & (A Ú B) = A.

Знание законов логики позволяет проверять правильность рассуждений и доказательств. Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.

Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), другие — основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).

Нарушения законов логики приводят к логическим ошибкам и вытекающим из них противоречиям.

Упрощение формул.

Пример 1. Упростить формулу (А Ú В) & (А Ú С).

Решение:

1. Раскроем скобки: (А Ú В) & (А Ú С) = A & A Ú A & C Ú B & A Ú B & C;

2. По закону идемпотентности A & A =A, следовательно, A & A Ú A & C Ú B & A Ú B & C = A Ú A & C Ú B & A Ú B & C;

3. В высказываниях А и А & C вынесем за скобки А и используя свойство А + 1= 1, получим A Ú A & C Ú B & A Ú B & C = A & (1 Ú C) Ú B & A Ú B & C = A Ú B & A Ú B & C;

4. Аналогично предыдущему пункту вынесем за скобки высказывание А. A Ú B & A Ú B & C = A & (1 Ú B) Ú B & C = A Ú B & C.

Таким образом, мы доказали закон дистрибутивности.

Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний — все отрицания будут применяться только к простым высказываниям.

Пример 2. Упростить выражения так, чтобы в полученных формулах не содержалось отрицания сложных высказываний.

Решение:

Законы алгебры логики и правила преобразования логических выражений

Примеры задач с решениями по этой теме Пройти тестирование по теме Контрольная по теме

Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.

Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.

Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).

Закон	Формулировка
1.Закон тождества Х = Х	Всякое высказывание тождественно самому себе.
2.Закон исключенного третьего X \/ ¬X = 1	Высказывание может быть либо истинным, либо ложным, третьего не дано. Следовательно, результат логического сложения высказывания и его отрицания всегда принимает значение «истина».
3.Закон непротиворечия X/\ ¬X = 0	Высказывание не может быть одновременно истинным и ложным. Если высказывание Х истинно, то его отрицание НЕ Х должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно.
4.Закон двойного отрицания ¬¬X = X	Если дважды отрицать некоторое высказывание, то в результате получим исходное высказывание.
5.Переместительный (коммутативный) закон X /\ Y = Y /\ X X /\ Y = YX /\	Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
6.Сочетательный (ассоциативный) закон (X \/Y) \/Z = X \/  (Y \/Z) (X/\Y)/\Z=X/\(Y/\Z)	При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
5.Распределительный (дистрибутивный) закон (X /\ Y) \/ Z= (X /\ Z) \/ (Y /\ Z) (X /\ Y) \/ Z =  (X \/ Z) /\ (Y \/ Z)	Определяет правило выноса общего высказывания за скобку.
7.Закон общей инверсии Закон де Моргана ¬(X \/ Y) = ¬X /\ ¬Y ¬(X /\ Y) = ¬X \/ ¬Y	Закон общей инверсии.
8.Закон равносильности (идемпотентности) A\/A= A; A/\ A = A.	от латинских слов idem — тот же самый и potens —сильный
9.Законы исключения констант: A\/ 1 = 1,     A\/ 0 = A; A/\1 = A,     A/\0 = 0.
10.Закон поглощения: A\/ (A/\B) = A; A/\ (A\/B) = A.
11.Закон исключения (склеивания): (A/\B) \/ (¬A/\B) = B; (A\/B)/\(¬A \/B) = B.
12.Закон контрапозиции (правило перевертывания): (A<=>B) = (B<=>A).
13.А => В = ¬A \/ В; 14.¬ (A=>B)=A/\B
14.А <=>В = (А /\ В) \/ (¬A /\ ¬B);
15.А <=>В = (¬A \/ В) /\ (А \/¬B).

Применим законы алгебры логики. Покажем на примере как можно упростить логическое выражение:

      1)(A/\B) \/ (A/\¬B) = A /\ (B \/ B)= A /\ 1 = A

      2)¬ (X \/ Y) /\ (X /\ ¬Y)

Законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами.

      ¬ (X \/ Y) /\ (X /\ ¬Y) = ¬ X /\ ¬Y /\ (X /\ ¬Y) = ¬ X /\ X/\¬Y /\¬Y= 0 ¬Y /\¬Y

3)применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией

      4)¬ X /\ Y \/ ¬ (X \/ Y) \/ X = ¬ X /\ Y \/ ¬ X /\ ¬Y \/ X= ¬ X /\ (Y \/ ¬Y) \/ X= ¬ X \/ X= 1

Логические основы работы компьютера

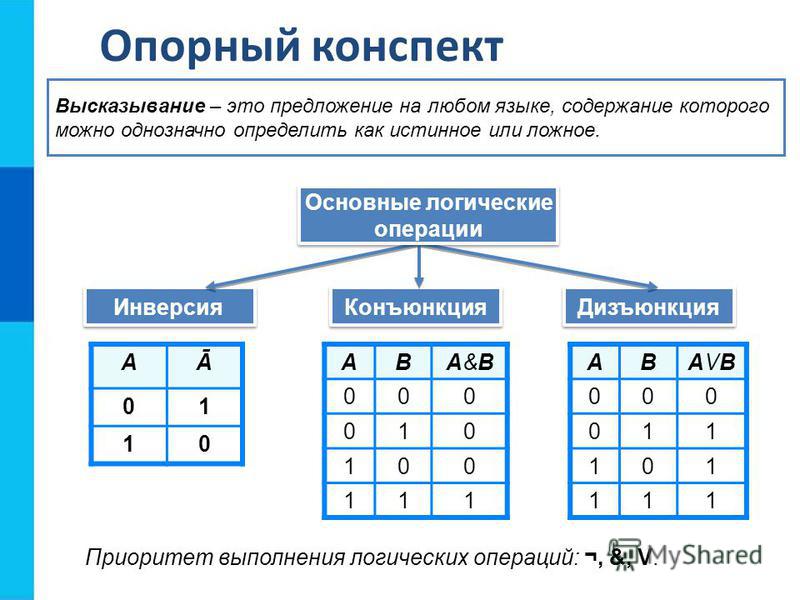
Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.

Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал.

Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».

Логический элемент «НЕ» (инвертор)

Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.

У этого элемента один вход и один выход. На функциональных схемах он обозначается:

Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.

Проверь соответствие логического элемента «НЕ» логическому элементу «НЕ». Воспользуйся тренажером Логические элементы.xlsx

Логический элемент «И» (конъюнктор)

Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.

Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:

Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.

Проверь соответствие логического элемента «И» логическому элементу «И».  Воспользуйся тренажером Логические элементы.xlsx

Логический элемент «ИЛИ» (дизъюнктор)

Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:

Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.

На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.

Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.

Проверь соответствие логического элемента «ИЛИ» логическому элементу «ИЛИ».  Воспользуйся тренажером Логические элементы.xlsx

Пример 1.Составьте логическую схему для логического выражения: F=A \/ B /\ A.

1.Две переменные – А и В.

2.Две логические операции: 1-/\, 2-\/.

3.Строим схему:

Пример 2.Постройте логическую схему, соответствующую логическому выражению F=А/\В\/ ¬(В\/А). Вычислить значения выражения для А=1,В=0.

1.Переменных две: А и В; 1 4 3 2

2.Логических операций три: /\ и две \/; А/\В\/ ¬ (В\/ А).

3.Схему строим слева направо в соответствии с порядком логических операций:

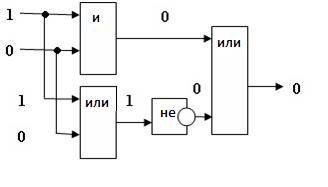
4.  Вычислим значение выражения: F=1 /\ 0 \/ ¬(0 \/ 1)=0

Построение таблиц истинности для логических выражений

Таблица истинности для логического выражения (функции) показывает соответствие всех возможных наборов значений логических переменных и значением выражения. Для наглядности и упрощения вычислений в таблицу добавляют столбцы логических операций,которые являются составными частями выражения.

Для того, чтобы построить таблицу истинности выражения нужно:

• Определить количество переменных, участвующих в выражении
• Определить количество составляющих выражение логических операций
• Заполнить строки таблицы всеми возможными наборами значений переменных. Наборы значений лучше представлять в виде двоичных чисел. Например, для трех переменных нужно заполнить восемь строк с 000 до 111.
• Вычислить и заполнить промежуточные операции в таблице
• Вычислить и заполнить значение логического выражения

Задача: Построить таблицу истинности для логического выражения \(  \overline{x} ⋅ y  + \overline{x + y} \)

Решение: 

Переменные	Промежуточные операции	Значение выражения
\( x \)	\( y \)	\( \overline{x} \)	\( \overline{x} ⋅ y \)	\( x + y \)	\( \overline{x + y} \)	\( \overline{x} ⋅ y  + \overline{x + y} \)
1	1	1
1	1	1	1	1
1	1
1	1	1

10.Стрелка Пирса

Стрелка
Пирса (логическое «ИЛИ-НЕ»)
высказываний a
и b
—
это новое высказывание, которое будет
истинно тогда и только тогда, когда оба
высказывания ложны.

Знаком
стрелки Пирса является ↓

Значения
функции стрелки
Пирса
представлены
в таблице:

Логическим
элементом операции стрелки
Пирса
является:

Стре́лка
Пи́рса
— бинарная логическая
операция, булева
функция над
двумя переменными. Введена в
рассмотрение Чарльзом
Пирсом (Сharles
Peirce) в 1880-1881 г.г.

Стрелка
Пирса, обычно обозначаемая ↓, эквивалентна
операции ИЛИ-НЕ и задаётся следующей
таблицей истинности:

Таким
образом, высказывание «X ↓ Y» означает
«ни X, ни Y». От перемены мест операндов
результат операции не изменяется.

		X ↓ Y

11.
Штрих Ше́ффера
— бинарнаялогическая
операция,булева
функциянад двумя переменными.
Введена в рассмотрениеГенри
Шефферомв 1913 г. (вотдельных
источниках именуется как Пунктир
Чулкова) Штрих Шеффера, обычно обозначаемый
|, эквивалентен операции И-НЕ и задаётся
следующей таблицей истинности:

Таким
образом, высказывание X | Y означает, что
X и Y несовместны, т.е. не являются истинными
одновременно. От перемены мест операндов
результат операции не изменяется.
Штрих Шеффера,
как и стрелка
Пирса,
образует базис для пространства булевых
функций от двух переменных. То есть
используя только штрих Шеффера можно
построить остальные операции. Например,

-отрицание

Дизъюнкция

Конъюнкция

Константа
1

В
электронике это означает, что для
реализации всего многообразия схем
преобразования сигналов, представляющих
логические значения, достаточно одного
типового элемента. С другой стороны,
такой подход увеличивает сложность
реализующих логические выражения схем
и тем самым снижает их надёжность.
Примером может являться промышленная
155 серия.

Элемент
2И-НЕ (2-in NAND), реализующий штрих Шеффера
обозначается следующим образом (по
стандартам ANSI):

В
европейских стандартах принято другое
обозначение:

12. Диодные
ключи.

Общие сведения. Электронный ключ — это
устройство, которое может находиться
в одном из двух устойчивых состояний:
замкнутом или разомкнутом. Основу
электронного ключа составляет нелинейный
активный элемент (полупроводниковый
диод, транзистор, тиристор и др.),
работающий в ключевом режиме. По типу
используемого нелинейного элемента
электронные ключи делятся на диодные,
транзисторные, тиристорные и т. д.

Диодные
ключи. Простейший
тип электронных ключей – диодные ключи.
В качестве активных элементов в них
используются полупроводниковые или
электровакуумные диоды.

При
положительном входном напряжении диод
открыт и ток через него

,
где —
прямое сопротивление диода.

Выходное
напряжение

.

Обычно ,
тогда.
При отрицательном входном напряжении
ток идет через диод

,

где —
обратное сопротивление диода.

При
этом выходное напряжение

.
Как правило, и.
При изменении полярности включения
диода график функцииповернется
на уголвокруг
начала координат.

Диодные
ключи не позволяют электрически разделить
управляющую и управляемые цепи, что
часто требуется на практике. Для
переключения (коммутации) напряжений
и токов служат т.н. диодные ключи. Эти
схемы позволяют при подаче определенного
управляющего напряжения замыкать/размыкать
электрическую цепь, по которой передается
полезный сигнал (ток, напряжение). В
простейших ключевых схемах в качестве
управляющего может использоваться сам
входной сигнал.

Говоря
о диодных ключах нельзя не упомянуть
особый класс полупроводниковых диодов
— p-i-n-диоды. Они применяются только для
коммутации ВЧ и СВЧ сигналов. Это возможно
благодаря их уникальному свойству —
регулируемой проводимости на частоте
сигнала. Такое регулирование осуществляется
обычно либо при подаче на диод внешнего
постоянного напряжения смещения, либо
непосредственно уровнем сигнала (для
ограничительных p-i-n-диодов).

Всего имеется пять законов алгебры логики:

zakondostatka.ru

составляем дизъюнкцию конъюнкций при условии, что если переменная входит в конъюнкцию со значением 1, то записываем эту переменную, если со значением 0, то ее отрицание. Получаем СДНФ.Теорема 2. Каждая булева функция от

переменных, не являющаяся тождественно истинной, может быть представлена в СКНФ, и притом единственным образом.Способы нахождения СКНФ1-й способ – с помощью равносильных преобразований: получаем одну из КНФ; если в полученной КНФ входящая в нее элементарная дизъюнкция

не содержит переменную

, то используем равносильность

и получаем две элементарных дизъюнкции; если в КНФ входят две элементарные дизъюнкции, то лишнюю можно отбросить.

Основные равносильности алгебры высказываний

С двумя из них мы только что познакомились, но ими дело, понятно, не огранивается. Тождеств довольно много и я перечислю самые важные и самые известные из них:

Коммутативность конъюнкции и коммутативность дизъюнкции

Коммутативность – это перестановочность:

Знакомые с 1-го класса правила: «От перестановки множителей (слагаемых) произведение (сумма) не меняется». Но при всей кажущейся элементарности этого свойства, справедливо оно далеко не всегда, в частности, некоммутативным является умножение матриц (в общем случае их  переставлять нельзя), а векторное произведение векторов – антикоммутативно (перестановка векторов влечёт за собой смену знака).

И, кроме того, здесь я снова хочу подчеркнуть формализм математической логики. Так, например, фразы «Студент сдал экзамен и выпил» и «Студент выпил и сдал экзамен» различны с содержательной точки зрения, но неразличимы с позиций формальной истинности. …Таких студентов знает каждый из нас, и из этических соображений мы не будет озвучивать конкретных имён =)

Ассоциативность логического умножения и сложения

Дистрибутивные свойства

Обратите внимание, что во 2-м случае будет некорректно говорить о «раскрытии скобок», в известном смысле здесь «фикция» – ведь их можно убрать вообще: , т.к. умножение – это более сильная операция

И опять же – эти, казалось бы, «банальные» свойства выполняются далеко не во всех алгебраических системах, и, более того, требуют доказательства (о которых мы очень скоро поговорим). К слову, второй дистрибутивный закон несправедлив даже в нашей «обычной» алгебре. И в самом деле:

Закон идемпотентности

Что делать, латынь….

Прямо какой-то принцип здоровой психики: «я и я – это я», «я или я – это тоже я» =)

И тут же несколько похожих тождеств:

…мда, что-то я даже подзавис… так и доктором философии завтра можно проснуться =)

Закон двойного отрицания

Ну а здесь уже напрашивается пример с русским языком – все прекрасно знают, что две частицы «не» означают «да». А для того, чтобы усилить эмоциональную окраску отрицания нередко используют три «не»: – даже с крохотным доказательством получилось!

 – «а был ли мальчик?» =)

В правом тождестве скобки можно опустить.

Законы де Моргана

Предположим, что строгий Преподаватель (имя которого вам тоже известно:)) ставит экзамен, если  – Студент ответил на 1-й вопрос и  – Студент ответил на 2-й вопрос. Тогда высказывание , гласящее о том, что Студент не сдал экзамен, будет равносильно утверждению  – Студент не ответил на 1-й вопрос или на 2-й вопрос.

Как уже отмечалось выше, равносильности подлежат доказательству, которое стандартно осуществляется с помощью таблиц истинности. В действительности мы уже доказали равносильности, выражающие импликацию и эквиваленцию, и сейчас настало время закрепить технику решения данной задачи.

Докажем тождество . Поскольку в  него входит единственное высказывание , то «на входе» возможно всего лишь два варианта: единица либо ноль. Далее приписываем единичный столбец и применяем к ним правило И:
В результате «на выходе» получена формула, истинность которой совпадает с истинностью высказывания . Равносильность  доказана.

Да, это доказательство является примитивным (а кто-то скажет, что и «тупым»), но типичный Преподаватель по матлогике вытрясет за него душу. Поэтому даже к таким простым вещам не стОит относиться пренебрежительно.

Теперь убедимся, например, в справедливости закона де Моргана .

Сначала составим таблицу истинности для левой части. Поскольку дизъюнкция находится в скобках, то в первую очередь выполняем именно её, после чего отрицаем столбец  :
Далее составим таблицу истинности для правой части . Здесь тоже всё прозрачно – в первую очередь проводим более «сильные» отрицания, затем применяем к столбцам  правило И:
Результаты совпали, таким образом, тождество  доказано.

Любую равносильность  можно представить в виде тождественно истинной формулы . Это значит, что ПРИ ЛЮБОМ исходном наборе нулей и единиц «на выходе» получается строго единица. И этому есть очень простое объяснение: так как таблицы истинности  и  совпадают, то, разумеется, они эквивалентны. Соединим, например, эквиваленцией левую и правую часть только что доказанного тождества де Моргана:
Или, если компактнее:

Задание 2

Доказать следующие равносильности:

а) ;

б)

Краткое решение в конце урока. Не ленимся! Постарайтесь не просто составить таблицы истинности, но ещё и чётко сформулировать выводы. Как я недавно отмечал, пренебрежение простыми вещами может обойтись очень и очень дорого!