Чем интуитивная логика отличается от формальной и как правильно делать умозаключения из утверждений «все мужики козлы» и «некоторые бабы дуры»

Отношения контрадикторности

Остановимся на самом главном вопросе – установлении истинной зависимости умозаключения по логическому квадрату.

Наиболее четко разграниченное и легко определяемое отношение между высказываниями – это отношение противоречия. Оба таких заключения не могут быть правдивыми или ложными одновременно. Правдивость одного исключает правдивость другого. Такие отношения подпадают под действие закона логики про исключение третьего:

Если умозаключение А, являющееся общим утвердительным, правдиво, то противоречащее ему частное отрицательное высказывание О обязательно неправдиво. То же правило проецируется и для отношений между общим отрицательным рассуждением Е и частным утвердительным І.

Блок 1. Суждения. Что такое суждения?

Суждение — это форма языкового мышления, которая состоит из понятий, связанных между собой, происходит утверждение либо отрицание чего-либо.

Пример:

• Федор Иванов работает менеджером по продажам.
• Некоторые менеджеры по продажам компании являются туристами.
• Никто из менеджеров по продажам не перевыполнил план продаж.

Суждения обладают набором свойств, которые в том числе отличают их от понятий.

1. Все суждения состоят из понятий, которые связаны между собой. Пример:

Понятие «Федор Иванов» и понятие «менеджер по продажам» образуют суждение «Федор Иванов работает менеджером по продажам».

2. Все суждения выражаются в форме предложения. Однако не любое предложение является суждением. Вопросительные и восклицательные предложения не являются суждениями, потому что в них ничего не утверждается и не отрицается. Повествовательное предложение всегда содержит утверждение или отрицание. Поэтому суждение выражается повествовательным предложением. Вместе с тем существуют риторические предложения, которые могут быть и вопросительными, и восклицательными по форме, в то время как по смыслу что – либо утверждают или отрицают. Примеры:

• И кто из менеджеров по продажам не стремится заработать бонусы?
• Вы сможете заработать свои бонусы, потому что их нельзя не заработать!

3. Все суждения можно разделить на истинные или ложные. Истинным является суждение, отражающее достоверное событие. Понятие «достоверное событие» определено в теории информации. Теория информации базируется на теории вероятности и математической статистике

Важно понимать, что здесь мы переходим к аппарату математической логики. В противном случае истинность или ложность суждения становятся уязвимы для критики, поскольку объем знаний отдельного субъекта в большинстве случаев не позволяет точно определить истинность/ложность события достоверно. Пример:

Никто из менеджеров по продажам не сможет выполнять план продаж в 10 млн руб.

Является это суждение ложным или истинным? Если менеджеры обычно продают на 1 млн. руб, то можно предположить, что суждение истинное. Однако, всегда остается вероятность того, что план продаж в 10 млн. руб. будет выполнен при случайном благоприятном стечении обстоятельств. И автор однажды столкнулся с таким «удивительным» событием, хотя математически ничего удивительного в этом нет.

В самых простых случаях, на бытовом уровне люди разделяют более-менее хорошо истинность/ложность суждений. Пример:

Все менеджеры по продажам нашей компании мужчины.

Если Вы получили такой опыт, что Вам оказались доступны к наблюдению первичные и вторичные половые признаки, то суждение будет истинным. Однако, если Вы делаете выводы на основании вторичных и третичных половых признаков, при этом не знаете, что такое трансгендерность, интерсексуальность, то можете допустить ошибку в своем суждении.

Формальная логика – это двузначная логика, когда все факты делятся только на истинные и ложные.

4. Все суждения могут быть сложными и простыми. Простые суждения с помощью союза объединяются в сложные.

Закон исключения третьего

Правила логического квадрата просты в запоминании и основываются на одном важном логическом законе – законе исключения третьего: если суждение с одной стороны истинно, то с другой – ложно и наоборот. Высказывание может быть или истинно, или ложно, и, соответственно, истинным или ложным будет его отрицание

Иных, третьих вариантов, не бывает. Высказывание «Все машины – красные» – ложно. Значит, высказывание «Не все машины – красные» — истинно. И здесь появляется волшебное слово «некоторые», которое почти всегда превратит ложное утверждение в истинное: «Некоторые машины – красные».

Отношения между категорическими суждениями. Умение обращаться с отношениями между суждениями

Поможем написать любую работу на аналогичную
тему

• Реферат

  От 250 руб

• Контрольная
  работа

  От 250 руб

• Курсовая работа

  От 700 руб

Получить выполненную работу или консультацию специалиста по вашему
учебному проекту

Узнать стоимость

Умение обращаться с отношениями между суждениями – важная составляющая логической культуры, позволяющая в общении, например в споре, легко находить суждения, следующие из данных суждений, противоречащие им и т.д. Это необходимо для развития аргументов в пользу своего тезиса и критики чужих тезисов и аргументов. Вступая в спор, нужно знать, какие суждения совместимы друг с другом, а какие – нет, к чему обязывает принятие тех или иных суждений, а к чему – нет и т.п.

Пример. Допустим, если кто-то пытается доказать, что все великие люди низкого роста, и вы в качестве возражения приводите суждение «Все великие люди высокого роста», будет нелегко и, скорее всего, невозможно отстоять это мнение. В то же время могут возникнуть другие вопросы. Например, если мы отрицаем суждение «Все великие люди низкого роста», обязывает ли это признать истинность суждения «Некоторые великие люди низкого роста» или «Все великие люди не низкого роста» и т.п.

Среди отношений между простыми суждениями наиболее важными являются отношения между категорическими суждениями.

Прежде всего, это отношения сравнимости-несравнимости. Категорические суждения называются сравнимыми, если их термины (субъект и предикат) совпадают с точностью до перестановки.

Пример. Суждения «Все студенты являются веселыми людьми» и «Все веселые люди являются студентами» — сравнимые.

Категорические суждения называются несравнимыми, если в одном из них есть термин, не входящий в другое.

Пример. Суждения «Все студенты являются веселыми людьми» и «Все студенты являются находчивыми людьми» — несравнимы.

Сравнимые суждения могут быть совместимыми и несовместимыми. Сравнимые категорические суждения называются совместимыми, если они могут быть вместе истинными.

Пример. Суждения «Все великие люди низкого роста» и «Некоторые великие люди низкого роста» — совместимые.

Сравнимые категорические суждения называются несовместимыми, если они не могут быть вместе истинными.

Пример. Суждения «Все великие люди низкого роста» и «Некоторые великие люди не являются людьми низкого роста» — несовместимые.

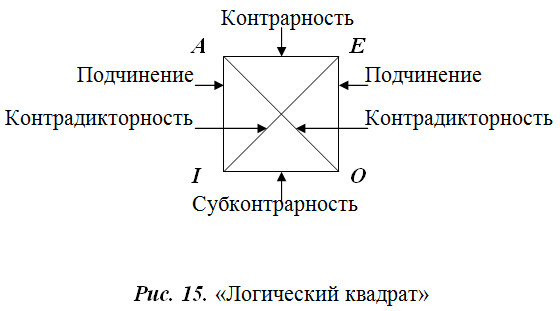
Отношения совместимости и несовместимости, в свою очередь, делятся на виды. Для систематизации и наглядного представления этих отношений еще в средние века был придуман так называемый «логический квадрат» (рис. 15).

К отношению совместимости относятся подчинение и субконтрарность (частичная совместимость).

Отношение подчинения имеет место между суждениями А и I, а также между Е и О. При этом суждения А (Е) называются подчиняющими, а суждения I (О) – подчиненными. Это отношение характеризуется следующим образом: если подчиняющее суждение А (Е) истинно, то подчиненное суждение I (О) истинно; если подчиненное суждение I (О) ложно, то подчиняющее суждение А (Е) ложно; подчиняющее и подчиненное суждения могут быть вместе ложны.

Субконтрарность имеет место между суждениями I и О. Эти суждения не могут быть вместе ложными. В то же время они могут быть вместе истинными, либо одно суждение может быть истинным, а другое – ложным.

К отношению несовместимости относятся контрадикторность (противоречие) и контрарность (противоположность). Отношение контрадикторности часто называют также отношением контрадикторной противоположности.

В отношении контрадикторности находятся суждения вида А и О, а также суждения вида Е и I. Контрадикторные суждения не могут быть вместе истинны и вместе ложны.

Контрарность имеет место между суждениями А и Е. Контрарные суждения не могут быть вместе истинными. В то же время они могут быть вместе ложными.

Рассмотренные отношения между простыми категорическими суждениями можно представить в виде схемы (рис. 16).

Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас

Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.

Расчет
стоимостиГарантииОтзывы

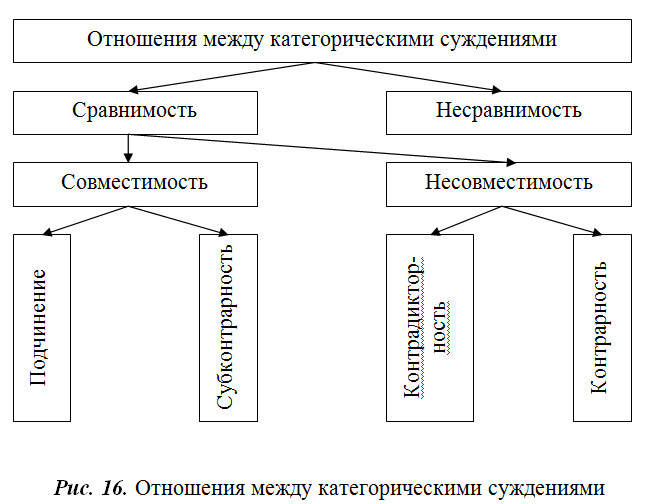
Использование логического квадрата для установки отношений между простыми рассуждениями

Выделяют такие виды взаимоотношений для категоричных умозаключений:

• контрадикторности или противоречия;
• контрарности или противоположности;
• субконтрарности или частичного совпадения;
• подчинения.

Кратко охарактеризовать различные отношения можно в форме таблицы.

Определить наглядно и запомнить, какие именно отношения по логическому квадрату возможны, поможет его описание. Итак, углы квадрата соотносят с видами умозаключений, а его диагонали и стороны определяют их взаимоотношения.

Почему логика — квадратная

Логика называется формальной потому, что работает с формой, а не содержанием, то есть с тем, как устроены предложения и как они между собой связаны. Это полезно тем, что мы можем отстраниться от смысла предложений, которые могут задевать наши чувства, и сделать правильное умозаключение без эмоционального влияния.

Давайте начнем с простых умозаключений, которые принято называть «умозаключениями по логическому квадрату».

Логика (на нашем начальном уровне) имеет дело с утвердительным предложениями — простыми суждениями, которые по двум признакам делятся на четыре группы.

2-й признак: качество

По качеству бывают утвердительные и отрицательные суждения.

Если мы объединим эти два признака, то получим четыре типа суждений, а в скобках укажем их классические обозначения:

Запомнить символьное обозначение классов суждений легко, если знать их происхождение от латинских слов “affirno” — утверждать и “nego” — отрицать, из которых были взяты гласные: первые — для общих суждений, вторые — для частных.

Вы уже догадались, что углы квадрата — четыре типа суждений. Часто его рисуют вот так:

Зачем нам нужен этот квадрат? Очень просто: он показывает, в каких отношениях находятся суждения разных классов. То есть с его помощью мы можем проверять себя, правильно ли мы делаем преобразования суждений, и выяснять, куда именно закралась ошибка.

Отношения подчинения

Характерной особенностью этих отношений является то, что истинность подчиненного высказывания зависит от истинности подчиняющего. Ложность общих умозаключений никак не соотносится с правдивостью частных, они могут быть как ложными, так и правдивыми в зависимости от ситуации.

Разберем на примере. «Все ученики ходят в школу» — общеутвердительное истинное высказывание. Значит, и суждение, находящееся у него в подчинении, «Некоторые ученики ходят в школу» тоже будет правдивым. Но при ложном общем суждении «Все школьники любят спорт», его подчиненное умозаключение «Некоторые школьники любят спорт» будет истинным.

Подводя итог, можно сказать, что знание отношений высказываний по логическому квадрату не только позволяет определить их правдивость или неправдивость, но и прийти к правильным выводам во время своих рассуждений или дискуссии с другими людьми.

Виды суждений

Логический квадрат, описывающий отношения между категорическими суждениями

В логическом квадрате все атрибутивные суждения делятся на:[источник не указан 93 дня]

Общеутвердительные, то есть вершина А («S — Р);

одновременно общие и утвердительные («Все S+ суть P-»), например: «Все слоны это млекопитающие»

Общеотрицательные, то есть вершина Е («S ~ Р)

общие и отрицательные («Ни один S+ не суть P+»), например: «Ни одно насекомое не есть млекопитающее»

Частноутвердительные, то есть вершина I ($S — Р);

частные и утвердительные («Некоторые S- суть P-»), например: «Некоторые животные млекопитающие»

Частноотрицательные, то есть вершина O ($S ~ Р).

частные и отрицательные («Некоторые S- не суть P+»), например: «Некоторые животные не млекопитающее»

Приведенные символы являются первыми и вторыми буквами латинских названий соответствующих суждений: «А» — от первой гласной буквы лат. Affirmo (утверждаю), «E» — от первой гласной буквы лат. Nego (отрицаю), «I» — от второй гласной буквы лат. Affirmo, «O» — от второй гласной буквы лат. Nego.[источник не указан 93 дня]

Отношения субконтрарности

Отношения частичного совпадения обратно по истинным значениям отношениям противности.

Отношения подпротивоположности не бывают неправдивыми одновременно, хотя бы одно из высказываний обязательно истинно, а бывает и так, что истинны оба.

То есть если взять за первое частное утвердительное высказывание І и предположить, что оно ложно, то в соответствии с логическим квадратом частично совпадающее с ним частное отрицательное высказывание О в обязательном порядке будет правдивым.

Рассмотрим на примере суждения «Все звери – зайцы». Оно, как мы помним, ложно. Следовательно, частично совпадающее высказывание будет правдивым. Проверим: «Некоторые звери – зайцы» — это правда.

Группы простых высказываний

Все простые сравнимые умозаключения можно условно распределить на две подгруппы:

1. Совместимые.
2. Несовместимые.

Выделяют три формы совместимости суждений.

Квадрат и крест

Для усвоения на слух правил логического квадрата также следует запомнить, что логику машины из вышеупомянутого утверждения называют субъектом, а красноту – предикатом. Предикат как атрибуция субъекта может быть глаголом или качеством. Или иным качеством, которое пристраивается к субъекту с использованием глагола-связки «суть». Выглядит логический квадрат, как квадрат. Это и неудивительно. Углы квадрата помечены литерами А, Е, I, O. А противоположно Е, I частично совместимо с O, I подчинено А, а Е главенствует над О. Квадрат перекрещен двумя линиями противоречий. Используя механику квадрата, можно работать с суждениями. Этот инструмент важен более лирикам, чем физикам, у физиков и так все строго, а лирики постоянно нуждаются в механизмах, позволяющих им подвергать сомнению и проверять истинность своих суждений. Конечно, в мире лжи и двусмысленности несколько потерялась красота истины и стремление к достижению ее любой ценой, но в некоторых случаях (в суде, в дорожном движении, в начислении заплаты) объективная истина имеет свою собственную ценность.

Мне помогло — и вам поможет, или Поспешное обобщение

Очень часто можно встретить примерно такие высказывания:

Что не так с этим умозаключением?

Мы не будем разбирать фактическую ошибку (иван-чай, тем более высушенный и заваренный, имеет мало чего полезного) или часто упоминающуюся ошибку «„после“ — не значит „вследствие“», а поговорим исключительно об ошибке, связанной с логическим квадратом.

Для этого нам из исходных предложений нужно получить формально-логические суждения.

Почему мы делаем первое суждение частноутвердительным, а второе — общеутвердительным? В первом случае речь идет об одном или нескольких людях, которым помог иван-чай, то есть не о целом классе предметов, не о всём множестве, не обо всех людях. Во втором же случае речь идет о случайном представителе людей, потому это можно принять за целое множество людей, которые имеют то же заболевание, что и тот, кому помогло, или вообще всех людей, если речь идет о панацее или повышении, стимуляции иммунитета, например. В некоторых случаях говорят именно так: мне помогло — значит, и всем поможет. Так мы и делаем общеутвердительное суждение.

Уже на этом этапе видна проблема обсуждаемого умозаключения: от частноутвердительного суждения происходит переход к общеутвердительному, что не соответствует их отношению подчинения.

2.7. Логические формулы

   Любое высказывание или целое рассуждение можно подвергнуть формализации. Это значит отбросить его содержание и оставить только его логическую форму, выразив её с помощью уже известных нам условных обозначений конъюнкции, нестрогой и строгой дизъюнкции, импликации, эквиваленции и отрицания.   Например, чтобы формализовать следующее высказывание: «
Он занимается живописью, или музыкой, или литературой», – надо сначала выделить входящие в него простые суждения и установить вид логической связи между ними. В приведённое высказывание входят три простых суждения:
«Он занимается живописью», «Он занимается музыкой», «Он занимается литературой».   Эти суждения объединены разделительной связью, однако они друг друга не исключают (можно заниматься и живописью, и музыкой, и литературой), следовательно, перед нами – нестрогая дизъюнкция, форму которой можно представить следующей условной записью:
a?
b?
c, где
a,
b,
c– указанные выше простые суждения. Форму:
a?
b?
c, можно наполнить каким угодно содержанием, например: «
Цицерон был политиком, или оратором, или писателем», «Он изучает английский, или немецкий, или французский», «Люди передвигаются наземным, или воздушным, или водным транспортом».   Формализуем рассуждение: «
Он учится в 9 классе, или в 10 классе, или в 11 классе. Однако, известно, что он не учится ни в 10, ни в 11 классе. Следовательно, он учится в 9 классе». Выделим простые высказывания, входящие в это рассуждение и обозначим их маленькими буквами латинского алфавита:
«Он учится в 9 классе (a)», «Он учится в 10 классе (b)», «Он учится в 11 классе (c)». Первая часть рассуждения представляет собой строгую дизъюнкцию этих трёх высказываний:
a?
b?
c. Вторая часть рассуждения является отрицанием второго: ¬
b, и третьего: ¬
c, высказываний, причём эти два отрицания соединяются, т. е. связаны конъюнктивно: ¬
b? ¬
c. Конъюнкция отрицаний присоединяется к упомянутой выше строгой дизъюнкции трёх простых суждений: (
a?
b?
c) ? (¬
b? ¬
c), и уже из этой новой конъюнкции как следствие вытекает утверждение первого простого суждения: «
Он учится в 9 классе». Логическое следование, как мы уже знаем, представляет собой импликацию. Таким образом, результат формализации нашего рассуждения выражается формулой: ((
a?
b?
c) ? (¬
b?¬
c)) ?
a. Эту логическую форму можно наполнить любым содержанием. Например: «
Впервые человек полетел в космос в 1957 г., или в 1959 г., или в 1961 г. Однако, известно, что впервые человек полетел в космос не в 1957 г. и не в 1959 г.. Следовательно, впервые человек полетел в космос в 1961 г.» Ещё один вариант: «
Философский трактат «Критика чистого разума» написал то ли Иммануил Кант, то ли Георг Гегель, то ли Карл Маркс. Однако, ни Гегель, ни Маркс не являются авторами этого трактата. Следовательно, его написал Кант».   Результатом формализации любого рассуждения, как мы увидели, является какая-либо формула, состоящая из маленьких букв латинского алфавита, выражающих входящие в рассуждение простые высказывания, и условных обозначений логических связей между ними (конъюнкции, дизъюнкции и др.). Все формулы делятся в логике на три вида:   1.
Тождественно-истинные формулыявляются истинными при всех наборах истинностных значений входящих в них переменных (простых суждений). Любая тождественно-истинная формула представляет собой логический закон.

Все или некоторые? Делаем правильные выводы

Обычно мы делаем логические преобразования со сложными для анализа суждениями. Но мы рассмотрим силу логического квадрата на примере содержательно простых суждений.

Предположим, что мы думаем так:

Какие выводы мы можем из этого сделать? Это общеутвердительное (А) суждение, следовательно, мы можем сказать, что:

— это тоже верное суждение, так как оно частноутвердительное (I) и (смотрим на квадрат) находится в отношении подчинения с A. Все отрицательные суждения при этом будут ложными, неправильными, так как они будут контрарными (общеотрицательные E) и контрадикторными (частноотрицательные O) по отношению к изначальному суждению (общеутвердительные A). То есть неправильно будет сказать «некоторые мужики — не козлы».

Несколько интереснее получается, если у нас исходное суждение частноутвердительное:

Можно ли из этого сделать вывод, что все бабы дуры? Нет, из частного нельзя вывести общее, только наоборот: отношение подчинения в квадрате — одностороннее! Вот так-то.

А что с отрицательными суждениями?