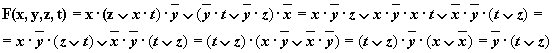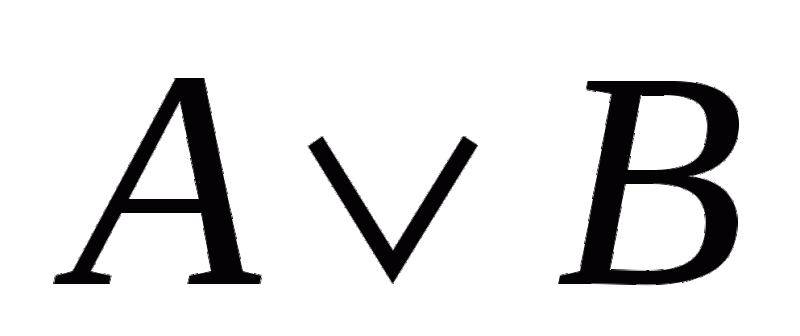Формальная логика

Презентация на тему: » Основы логики 1. Формы мышления. Основоположником формальной логики является Аристотель. Логика – это наука о законах и формах мышления. Это учение о.» — Транскрипт:

1

Основы логики 1. Формы мышления

2

Основоположником формальной логики является Аристотель. Логика – это наука о законах и формах мышления. Это учение о способах рассуждений и доказательств. Понятие – это форма мышления, которая выделяет существенные признаки предмета или класса предметов, позволяющие отличать их от других. Высказывание – это формулировка своего понимания окружающего мира. Высказывание является повествовательным предложением, в котором что-либо утверждается или отрицается.

3

1.Какой длины эта лента? 2.Прослушайте сообщение. 3.Делайте утреннюю зарядку! 4.Назовите устройство ввода информации. 5.Кто отсутствует? 6.Париж – столица Англии. 7.Число 11 является простым =10 9.Без труда не вытащишь и рыбку из пруда. 10.Сложите числа 2 и Некоторые медведи живут на севере. 12.Все медведи – бурые.

4

Какие из следующих предложений являются высказываниями? Определите их истинность. 1.Число 6 – чётное. 2.Посмотрите на доску. 3.Все роботы являются машинами. 4.У каждой лошади есть хвост

5.Внимание! 6.Выразите 1 час 15 минут в минутах. 7.Наполеон был французским императором

8.Чему равно расстояние от Земли до Марса? 9.Не нарушайте правил дорожного движения! 10.Невозможно создать вечный двигатель.

5

Высказывания бывают общими, частными или единичными. Общее – все, всякий, каждый, ни один. Частное – некоторые, большинство и т.п. Единичное – во всех остальных случаях.

6

Какие из приведённых высказываний являются общими? Определите их истинность. 1.Не все книги содержат полезную информацию. 2.Кошка является домашним животным. 3.Все солдаты храбрые. 4.Ни один внимательный человек не совершит оплошность. 5.Некоторые ученики двоечники. 6.Все ананасы приятны на вкус. 7.Мой кот страшный забияка. 8.Любой неразумный человек ходит на руках.

7

Какие из приведённых высказываний являются частными? Определите их истинность. 1.Некоторые мои друзья собирают марки. 2.Все лекарства неприятны на вкус. 3.Некоторые лекарства приятны на вкус. 4.А – первая буква в алфавите. 5.Некоторые медведи – бурые. 6.Тигр – хищное животное. 7.У некоторых змей нет ядовитых зубов. 8.Многие растения обладают целебными свойствами. 9.Все металлы проводят тепло.

8

Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение (знание или вывод).

9

2. Логические выражения и операции Логическая переменная – это простое высказывание, содержащее только одну мысль. Символическое обозначение – латинская буква (например, А,В, Х и т.д.). Значением логической переменной могут быть только константы ИСТИНА и ЛОЖЬ (1 и 0). Операция — это некоторый закон, по которому одному или нескольким значениям, называемым операндами, ставится в соответствие одно значение, называемое результатом. Операции, имеющие один операнд, называются унарными, имеющие два операнда – бинарными.

10

Название Обозначение Союз в естественном языке Конъюнк- ция (от лат. conjunctio — связываю) Логическое умножение А&В или А^В А и В Дизъюнк- ция (от лат. disjuctio — различаю) Логическое сложение АνВАνВ А или В Инверсия (от лат. inversio – переворачи- ваю) Отрицание Ā или ¬А Не А Имплика- ция (от лат. implicatio – тесно связывать) Логическое следование АВ А – условие В — следствие Если А, то В; когда А, тогда В Эквивалент- ность (от лат. аeguivalens — равноценное) Логическое равенство АВ или АВ А тогда и только тогда, когда В АВ А^ВА^В АВ АνВАνВ А Ā АВ А В АВ Таблица истинности – это таблица, определяющая значение сложного высказывания при всех возможных значениях простых высказываний

11

Логическая функцияэтосоставное высказывание, которое содержит несколько простых мыслей, соединенных между собой с помощью логических операций. Логическая функция – это составное высказывание, которое содержит несколько простых мыслей, соединенных между собой с помощью логических операций. Порядок выполнения действий: 1.действия в скобках; 2.инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.

12

Записать в виде логического выражения следующее высказывание: «Летом Петя поедет в деревню и, если будет хорошая погода, то он пойдёт на рыбалку». 1) Проанализируем составное высказывание. А = Петя поедет в деревню; В = Будет хорошая погода; С = Он пойдёт на рыбалку. 2) Запишем высказывание в виде логического выражения, учитывая порядок действий. Если необходимо, расставим скобки: F = A^(BC)

13

Записать в виде логического выражения следующие высказывания: 1.Число 17 нечётно и двузначное. 2.Водительские права можно получить тогда и только тогда, когда тебе исполнится 18 лет. 3.Компьютер выполняет вычисления, если он включен.

Формальная логика (ред. Чупахин И.Я., Бродский И.Н.)

Название:  Формальная логика

Под редакцией: Чупахин И.Я., Бродский И.Н.

Ленинград: Издательство Ленинградского университета, 1977.- 357 с.DjVu 3,77 Мб

Качество: сканированные страницы, текстовый слой

Язык: Русский

В основу учебника положен курс логики, читавшийся на философском факультете Ленинградского университета в течение ряда лет. В нем освещаются вопросы, относящиеся к общей и символической логике. Учебник предназначен для студентов-философов и студентов других гуманитарных факультетов и педагогических вузов.

Введение 3 § 1. Марксистская философия о мышлении — § 2. Мышление и язык 4 § 3. Определение формальной логики 5 § 4. Логика и психология 9 § 5. Из истории логики 10 § 6. Практическое значение формальной логики 16 § 7. Структура формальной логики 19

Часть первая. ОБЩАЯ ЛОГИКА. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ФОРМЫ И МЕТОДЫ МЫШЛЕНИЯ

 
Глава I. Понятие§ 8. Об определении и структуре понятия§ 9. Основные методы образования понятий§ 10. Соотношение между содержанием и объемом понятия§ 11. Виды понятий§ 12. Формально-логические отношения между понятиями по содержанию и по объему § 13. Обобщение и ограничение понятийГлава II. Суждение§ 14. Сущность суждения и его строение§ 15. Суждение и предложение § 16. Суждение и вопрос § 17. Деление суждений по качеству и количеству§ 18. Объединенная классификация суждений по качеству и количеству§ 19. Распределеиность терминов в категорических суждениях§ 20. Отношения между суждениями§ 21. Деление суждений по модальности§ 22. Сложные сужденияГлава III. Основные формально-логические законы§ 23. Обшие замечания § 24. Закон тождества§ 25. Закон противоречия§ 26. Закон исключенного третьего§ 27. Закон достаточного основания Глава IV. Умозаключение § 28. Определение умозаключения§ 29. Непосредственные умозаключения § 30. Простой категорический силлогизм § 31. Сокращенные, сложные и сложносокращенные категорические силлогизмы§ 32. Условные, разделительные и условно-разделительные силлогизмы§ 33. Индуктивные умозаключения § 34. АналогияГлава V. Логические методы научного мышления§ 35. Методы классификации объектов исследования§ 36. Определение§ 37. Доказательство§ 38. Доказательство (продолжение: паралогизмы, софизмы и парадоксы)§ 39. Аксиоматический метод§ 40. Индуктивные методы установления причинной связи явлений § 41. Гипотеза§ 42. Вероятностные методы в логикеЧасть вторая. СИМВОЛИЧЕСКАЯ ЛОГИКАГлава I. Табличное построение логики высказываний§ 1. Высказывания и формы высказываний§ 2. Язык логики высказываний§ 3. Семантика логических знаков§ 4. Таблицы формул логики высказываний§ 5. Равносильные формулы § 6. Правило равносильной замены § 7. Полные системы логических знаков§ 8. Закон двойственности§ 9. Тождественно-истинные и тождественно-ложные формулы Глава II. Нормальные формы формул логики высказываний§ 10. Нормальная форма§ 11. Проблема разрешения§ 12. Конъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма§ 13. Логическое следование и логические следствия§ 14. Сокращенная конъюнктивная нормальная форма§ 15. Дизъюнктивные нормальные формыГлава III. Естественный вывод в логике высказываний§ 16. Понятия логического вывода§ 17. Производные правила§ 18. Чисто прямое доказательство§ 19. Слабое косвенное доказательство§ 20. Квазисильное косвенное доказательство§ 21. Сильное (классическое) косвенное доказательство§ 22. Полнота классического нечисления высказываний§ 23. Аксиоматическое представление логики высказыванийГлава IV. Формализованная силлогистикаГлава V. Естественный вывод в логике предикатовГлава VI. Модальная логика

• Назад

• Вперёд

Споры вокруг формальной логики в Советском Союзе

В 1930—1940-е годы формальная логика третировалась официальными философскими инстанциями как «теоретическая основа буржуазного мировоззрения», нечто несовместимое с марксизмом и коммунистическими идеалами. Активной работы в соответствующих направления не было, традиции были утрачены, немногие остававшиеся в живых специалисты были вынуждены заниматься другими дисциплинами или были лишены условий для нормального научного общения.

Ситуация несколько изменилась в — годах, когда (по некоторым сведениям, по личному распоряжению И. В. Сталина) логика была введена в состав школьной программы (был написан ряд учебников (В. Ф. Асмуса, К. С. Бакрадзе, М. С. Строговича) и даже в сокращенном или переработанном виде переизданы «буржуазные» учебники С. Н. Виноградова и Г. И. Челпанова). За этим последовало создание кафедры логики на Философском факультете Московского университета (в качестве одного из кандидатов на занятие кафедры рассматривался А. Ф. Лосев, хотя в конце концов занял её П. С. Попов), издание ряда книг по формально-логической тематике и некоторые другие мероприятия.

Однако вокруг этой тематики с переменным успехом продолжалась борьба «диалектиков» и «формалистов». В 1950—1960-е годы формальная логика (уже уйдя из школы) обосновалась в вузах и исследовательских институтах. Выдающуюся роль в восстановлении логических исследований и преподавания логики в стране сыграли такие представители формалистического направления, как С. А. Яновская, А. С. Есенин-Вольпин, Ю. А. Гастев, А. А. Марков и др.

Обратной стороной процесса стала контрреакция со стороны «формалистов» по отношению к логикам, стремившимся разрабатывать логику вне программы её формализации. Уже в 1960—1970-е годы сложности с публикациями испытывали такие логики, как А. А. Зиновьев (вынужденный затем сменить язык и перейти на «математические» символы), Э. В. Ильенков (покинувший коллектив «Философской энциклопедии» в знак протеста против подмены логической проблематики математической) и др.

До некоторой степени эта реакция продолжается даже в постсоветские годы.

Предмет и метод формальной логики

Предмет формальной логики специально реконструировался и критиковался в работах Московского логического кружка

и затем Московского методологического кружка
. Критика касалась не уместности разработки формальной логики как таковой или её полезности, а полноты исчерпания ею логической проблематики и её претензий на роль теории мышления.

Согласно реконструкции, проведённой в ММК, логика имеет дело с «языковым мышлением» (или, «языком, взятым в функции мышления»), в котором группы определённым образом связанных между собой знаков по определённым законам замещают реальные объекты и друг друга в отношении к действиям:

объективное содержание ────────────── знаки языка

связь значения

Формальная логика возможна, когда в качестве замещаемого содержания выступают не непосредственно объекты действия, а, в свою очередь, знаки, образующие замкнутые оперативные системы. Метод формальной логики последовательно проводит принцип параллелизма формы и содержания мышления.

Развитие символизации в формальной логике и её превращение в одну из математических дисциплин закономерны, естественны и неизбежны.

Претензии формальной логики на роль теории мышления несостоятельны, поскольку:

• её понятия описывают не мышление в целом, а лишь его знаковую форму, и то неполно;
• в её понятиях не учитывается зависимость строения и правил преобразования этой формы от содержания;
• её понятия не отражают различия между мышлением и его продуктами, (знаниями);
• её понятия не могут объяснить образование сложных знаний;
• её метод несовместим с историческим подходом к исследованию мышления.

Споры вокруг формальной логики в Советском Союзе

В 1930—1940-е годы формальная логика третировалась официальными философскими инстанциями как «теоретическая основа буржуазного мировоззрения», нечто несовместимое с марксизмом и коммунистическими идеалами. Активной работы в соответствующих направления не было, традиции были утрачены, немногие остававшиеся в живых специалисты были вынуждены заниматься другими дисциплинами или были лишены условий для нормального научного общения.

Ситуация несколько изменилась в — годах, когда (по некоторым сведениям, по личному распоряжению И. В. Сталина) логика была введена в состав школьной программы (был написан ряд учебников (В. Ф. Асмуса, К. С. Бакрадзе, М. С. Строговича) и даже в сокращенном или переработанном виде переизданы «буржуазные» учебники С. Н. Виноградова и Г. И. Челпанова). За этим последовало создание кафедры логики на Философском факультете Московского университета (в качестве одного из кандидатов на занятие кафедры рассматривался А. Ф. Лосев, хотя в конце концов занял её П. С. Попов), издание ряда книг по формально-логической тематике и некоторые другие мероприятия.

Однако вокруг этой тематики с переменным успехом продолжалась борьба «диалектиков» и «формалистов». В 1950—1960-е годы формальная логика (уже уйдя из школы) обосновалась в вузах и исследовательских институтах. Выдающуюся роль в восстановлении логических исследований и преподавания логики в стране сыграли такие представители формалистического направления, как С. А. Яновская, А. С. Есенин-Вольпин, Ю. А. Гастев, А. А. Марков и др.

Обратной стороной процесса стала контрреакция со стороны «формалистов» по отношению к логикам, стремившимся разрабатывать логику вне программы её формализации. Уже в 1960—1970-е годы сложности с публикациями испытывали такие логики, как А. А. Зиновьев (вынужденный затем сменить язык и перейти на «математические» символы), Э. В. Ильенков (покинувший коллектив «Философской энциклопедии» в знак протеста против подмены логической проблематики математической) и др.

До некоторой степени эта реакция продолжается даже в постсоветские годы.

Программа «логистики»

Формалистами (представителями т. н. «логистики», оформившейся на Женевском конгрессе г. усилиями Л. Кутюра, А. Лаланда и др.) конца XIX — начала XX века формальность логики связывалась с выделением значений истинности высказываний при переносе их из естественного языка в символическую нотацию. Логистики стремились дать обоснование математическому знанию (в перспективе — естествознанию) в пределах одной только формальной логики. Существенные усилия в этом направлении были приложены Д. Гильбертом, Кутюра, Б. Расселом.

Фокус на истинностном значении отличал формальную логику от других дисциплин, имеющих дело с формой, как то: лингвистика и такие математические дисциплины, как арифметика, геометрия, алгебра, математический анализ. Соответственно, к формальной логике ими относились все те разделы логики, которые удалось формализовать в символических формах, разработанных в XIX—начале XX век математиками и логиками О. де Морганом, Дж. Булем, Дж. Пеано, Г. Фреге, Расселом и другими.

«За бортом» формальной логики оставались такие логические дисциплины, как диалектика (в её средневековой версии и различных нововременных вариантах), индуктивная логика (Дж. С. Милль) и другие варианты логики науки.

Так понимаемая формальная логика переставала быть наукой о мышлении, и многими формалистами последнее вовсе дезавуировалось как «психологическое» понятие, не имеющее отношения к логике как таковой, которая должна сосредоточиться на изучении и совершенствовании языка, на структурных, а не процессуальных свойствах речевых конструкций. Эта точка зрения нашла развитие во взглядах Венского кружка, Львовско-Варшавской школы и, далее, англосаксонской аналитической философии. Однако другими формалистами она не разделялась.

В то же время в 1910—20-х гг. претензии логистиков на обоснование точного знания критиковались А. Пуанкаре и, позднее, примкнувшим к нему в этой критике Гильбертом, после чего логистическое движение сошло на нет.

Примечания

1. , p. 2.
2. .
3. , с. 576.
4. Кант И. Критика чистого разума. — М.: 1994. — С. 14.
5. Кант И. Цит. соч. — С. 72—73.
6. Scholz H. Concise History of Logic. — New York, .
7. Carnap R. Induktive Logik und Wahrscheinlichkeit. — Wien, 1958. — С. 31.
8. Лукасевич Я. Аристолевская силлогистика с точки зрения современной формальной логики. — М., 1959. — С. 48—49.
9. Пуанкаре А. О науке. — М.: Наука, 1983. — С. 475—518, 580—616. — 736 с.
10. Зиновьев А. А. Восхождение от абстрактного к конкретному (на материале «Капитала» К. Маркса). — М., 2002. — 321 с.;
    ;
    ;
    ;
    Ладенко И. С. Об отношении эквивалентности и его роли в некоторых процессах мышления // Доклады АПН РСФСР. — 1958. — № 1.;
    Ладенко И. С. О некоторых процессах мышления, связанных с установлением отношения эквивалентности // Доклады АПН РСФСР. — 1958. — № 2.
    Швырёв В. С. К вопросу о путях логического исследования мышления // Доклады АПН РСФСР. — 1960. — № 2. и др.

11. ;
    ;
    ;
    Щедровицкий Г. П. О взаимоотношении формальной логики и неопозитивистской «логики науки» // Диалектический материализм и современный позитивизм : Сб. — М., 1961.;

12. Щедровицкий Г. П. О методе исследования мышления. — М., 2006. — С. 110—183. — 600 с.. См. тж. и Щедровицкий Г. П. Проблемы логики научного исследования и анализ структуры науки / Из архива Г. П. Щедровицкого. Т. 7. — М., 2004. — 400 с.
13. Łukasiewicz J., Tarski A. Untersuchungen über den Aussagenkalkül // Sprawozdania z posiedzec Towarzystwa Naukowego Warszawskiego. Wydział II. R. XXIII. — Warszawa, 1930.
14. Формальная логика // Розенталь М., Юдин П. (ред.). Краткий философский словарь. — М.: .
15. Ладенко И. С. Становление и развитие идей генетической логики // Вопросы методологии, 1991, № 3.
16. ↑
17. Постановление ЦК ВКП(б) от 03.12.46 «О преподавании логики и психологии в средней школе».
18. «Основы теоретической логики» Гильберта и В. Аккермана (1947), «Опыт исследования значения логики» Ш. Серрюса (), «Введение в логику и методологию дедуктивных наук» А. Тарского (1948) и др.

Современность

В конце XIX — начале XX веков были заложены основы т. н. математической, или символической, логики. Её суть заключается в том, что для обнаружения истинностного значения выражений естественного языка можно применять математические методы. Именно использование символической логики отличает современную логическую науку от традиционной.

Огромный вклад в развитие символической логики внесли такие учёные, как Дж. Буль, О. де Морган, Г. Фреге, Ч. Пирс и др. В XX веке математическая логика оформилась в качестве самостоятельной дисциплины в рамках логической науки.

Начало XX века ознаменовалось становлением идей неклассической логики, многие важные положения которой были предвосхищены и/или заложены Н. А. Васильевым и И. Е. Орловым.

В середине XX века развитие вычислительной техники привело к появлению логических элементов, логических блоков и устройств вычислительной техники, что было связано с дополнительной разработкой таких областей логики, как проблемы логического синтеза, логическое проектирование и логического моделирования логических устройств и средств вычислительной техники.

В 80-х годах XX века начались исследования в области искусственного интеллекта на базе языков и систем логического программирования. Началось и создание экспертных систем с использованием и развитием автоматического доказательства теорем, а также методов доказательного программирования для верификации алгоритмов и программ для ЭВМ.

В 80-е годы начались также изменения в образовании. Появление персональных компьютеров в средних школах привело к созданию учебников информатики с изучением элементов математической логики для объяснения логических принципов работы логических схем и устройств вычислительной техники, а также принципов логического программирования для компьютеров пятого поколения и разработка учебников информатики с изучением языка исчисления предикатов для проектирования баз знаний.

Приложения логики

Прикладные проблемы логики (см. Прикладная логика) и логической семантики

• Приложения логики в методологии науки
• Приложения логики в философии
• Приложения логики в теологии
• Приложения логики в психологии
• Приложения логики в правовых науках
• Приложения логики в лингвистике
• Приложения логики в других дисциплинах
• Искусственный интеллект

Приложения логики в анализе познавательных процедур

Логический анализ форм и приёмов познания

• Формы мышления
• Определение
• Классификация
• Абстракция
• Идеализация
• Аксиоматизация
• Формализация
• Логические проблемы аргументации
• Логика доказательств

Приложения логики в философии

• Приложения логики в философии
• Приложения логики в онтологии
• Приложения логики в эпистемологии
• Приложения логики в этике
• Логические проблемы аргументации (теория аргументации)
• Аналитическая философия

Приложения логики в психологии

• Когнитивная наука
• Когнитивная психология
• Логика открытий

Поскольку логика устанавливает законы и схемы мышления, существует проблема соотнесения логики с творчеством, которое опирается на интуицию. Творчество без ограничений является идеализацией: оно ограничено психологическими закономерностями восприятия или, например, законами композиции в изобразительном искусстве. Творчество предполагает не только способность выдвинуть интересную идею, но и умение убедительно обосновать её и претворить в жизнь по определённым правилам, следовательно, должно следовать каким-то правилам мышления.

Приложения логики в компьютерных науках

• Динамические логики (динамическая логика)
• Логики программ (логика программ)
• Логика экспертных систем (логики экспертных систем)
• Логика в информатике
• Доказательное программирование
• Автоматическое доказательство теорем
• Логическое программирование

Литература

Исследования

• Гуссерль Э. Логические исследования. Т. 1 // Философия как строгая наука. — Новочеркасск: Сагуна, 1994. — 357 с. — ISBN ISBN 5-7593-0138-1.
• Васильев Н. А. Воображаемая логика. Избранные труды. — Наука, 1989. — 264 с. — 6200 экз. — ISBN 5-02-007946-4.

Учебная и справочная литература

• Ивлев Ю. В. Учебник логики: Семестровый курс: Учебник. — М.: Дело, 2003. — 208 с — ISBN 5-7749-0317-6
• Бочаров В. А., Маркин В. И. Основы логики: Учебник. — М.: ИНФРА-М, 2001. — 296 с. — ISBN 5-16-000496-3

Литература по истории логики

• Бажанов В. А. История логики в России и СССР. — М.: Канон+, 2007. — 336 с. — ISBN 5-88373-032-9
• Попов П. С. История логики нового времени. — М., Издательство МГУ, 1960.
• Стяжкин Н. И. Формирование математической логики. — М., 1967.
• Scholtz H. Geschichte der Logik, 1931. (Concise History of Logic. — New York, 1961).

Литература по китайской логике

• Спирин B. C. О «третьих» и «пятых» понятиях в логике древнего Китая // Дальний Восток. Сборник статей по филологии, истории, философии. — М., 1961.
• Кроль Ю. Л. Спор как явление культуры древнего Китая // Народы Азии и Африки. — 1987. — № 2.
• Крушинский А. А. Имена и реалии в древнекитайской логике и методологии (Обзор) // Современные историко-научные исследования: наука в традиционном Китае. — М., 1987.
• Пань Шимо (КНР). Логика Древнего Китая (краткий очерк) // Философские науки. — 1991. — № 12.
• Чжоу Юньчжи. Основные вехи развития древнекитайской логики мин бянь, её главные особенности и реальные достижения // Рационалистическая традиция и современность. Китай. 1993. №. — С. 152—178.
• Крушинский А. А. Логика «И цзина». Дедукция в древнем Китае. — М., 1999.
• Кварталова Н. П. Логические идеи трактата «Гунсунь Лун-цзы» // Человек и духовная культура Востока. Альманах. Вып. I. — М., 2003. — С. 167—172.
• Кобзев А. И. Школа имен (мин цзя): коллизия логики и диалектики // Китай в диалоге цивилизации: К 70-летию академика М. Л. Титаренко. — М. 2004. — С. 550—557.