Логические элементы
Содержание:
- Классическая логика
- Булева логика
- Примечания
- Инвертор
- Логический вентиль
- Многозначная логика
- Логическая функция «И» (умножение)
- Связь с естественным языком
- Связь с естественным языком
- Обозначения
- Применение логоческих элементов
- 3.1. Что такое алгебра логики
- Логический элемент «ИЛИ»
- Логический элемент «И-НЕ»
- Обозначения
- Логическая функция «НЕ» (отрицание)
- Примечания
Классическая логика
В классическом исчислении высказываний свойства дизъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства дизъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для дизъюнкции:
- a→a∨b{\displaystyle a\to a\lor b}
- b→a∨b{\displaystyle b\to a\lor b}
- (a→c)→((b→c)→((a∨b)→c)){\displaystyle (a\to c)\to ((b\to c)\to ((a\lor b)\to c))}
С помощью этих аксиом можно доказать другие формулы, содержащие операцию дизъюнкции
Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
Булева логика
В булевой логике импликация — это функция двух переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {,1}{\displaystyle \{0,1\}}. Результат также принадлежит множеству {,1}{\displaystyle \{0,1\}}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений ,1{\displaystyle 0,1} может использоваться любая другая пара подходящих символов, например false,true{\displaystyle \operatorname {false} ,\operatorname {true} } или F,T{\displaystyle F,T} или «ложь», «истина».
Правило:
- Импликация как булева функция ложна лишь тогда, когда посылка истинна, а следствие ложно. Иными словами, импликация A→B{\displaystyle A\to B} это сокращённая запись для выражения ¬A∨B{\displaystyle \neg A\lor B}.
Таблицы истинности:
прямая импликация
(от a к b) (материальная импликация (англ.)русск., материальный кондиционал (англ.)русск.)
-
a{\displaystyle a} b{\displaystyle b} a→b,a⩽b{\displaystyle a\to b,a\leqslant b} {\displaystyle 0} {\displaystyle 0} 1{\displaystyle 1} {\displaystyle 0} 1{\displaystyle 1} 1{\displaystyle 1} 1{\displaystyle 1} {\displaystyle 0} {\displaystyle 0} 1{\displaystyle 1} 1{\displaystyle 1} 1{\displaystyle 1}
- если первый операнд не больше второго операнда, то 1,
- если a⩽b{\displaystyle a\leqslant b}, то истинно (1).
«Житейский» смысл импликации.
Для более лёгкого понимания смысла прямой импликации и запоминания её таблицы истинности может пригодиться житейская модель:
- А — начальник. Он может приказать «работай» (1) или сказать «делай что хочешь» (0).
- В — подчинённый. Он может работать (1) или бездельничать (0).
В таком случае импликация — не что иное, как послушание подчинённого начальнику.
По таблице истинности легко проверить, что послушания нет только тогда, когда начальник приказывает работать, а подчинённый бездельничает.
обратная импликация (от b к a, A∨(¬B){\displaystyle A\lor (\neg B)})
-
a{\displaystyle a} b{\displaystyle b} a←b,a⩾b{\displaystyle a\leftarrow b,a\geqslant b} {\displaystyle 0} {\displaystyle 0} 1{\displaystyle 1} {\displaystyle 0} 1{\displaystyle 1} {\displaystyle 0} 1{\displaystyle 1} {\displaystyle 0} 1{\displaystyle 1} 1{\displaystyle 1} 1{\displaystyle 1} 1{\displaystyle 1}
- если первый операнд не меньше второго операнда, то 1,
- если a⩾b{\displaystyle a\geqslant b}, то истинно (1).
Обратная импликация — отрицание (негация, инверсия) обнаружения увеличения (перехода от 0 к 1, инкремента).
отрицание (инверсия, негация) прямой импликации
-
a{\displaystyle a} b{\displaystyle b} ¬(a→b),a>b{\displaystyle \lnot (a\to b),a>b} {\displaystyle 0} {\displaystyle 0} {\displaystyle 0} {\displaystyle 0} 1{\displaystyle 1} {\displaystyle 0} 1{\displaystyle 1} {\displaystyle 0} 1{\displaystyle 1} 1{\displaystyle 1} 1{\displaystyle 1} {\displaystyle 0}
- если первый операнд больше второго операнда, то 1,
- если a>b{\displaystyle a>b}, то истинно (1).
отрицание (инверсия, негация) обратной импликации (¬A∧B{\displaystyle \lnot A\land B}),
разряд займа в .
-
a{\displaystyle a} b{\displaystyle b} ¬(a←b),a<b{\displaystyle \lnot (a\leftarrow b),a<b} {\displaystyle 0} {\displaystyle 0} {\displaystyle 0} {\displaystyle 0} 1{\displaystyle 1} 1{\displaystyle 1} 1{\displaystyle 1} {\displaystyle 0} {\displaystyle 0} 1{\displaystyle 1} 1{\displaystyle 1} {\displaystyle 0}
- если первый операнд меньше второго операнда, то 1,
- если a<b{\displaystyle a<b}, то истинно (1).
Другими словами, две импликации (прямая и обратная) и две их инверсии — это четыре оператора отношений. Результат операций зависит от перемены мест операндов.
Примечания
- ↑ , с. 264—266, 534—536.
- . // Website Online Etymology Dictionary. Дата обращения 7 февраля 2016.
- , с. 67.
- Стяжкин Н. И. . Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 321, 348, 352, 368.
- . // Website Jeff Miller Web Pages. Дата обращения 7 февраля 2016.
- , с. 30.
- Пратт Т. . Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
- Грогоно П. . Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
- Вегнер П. . Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
- , Строуструп Б. . Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
- Яблонский С. В. . Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
- Рвачёв В. Л. . Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.
- ↑ Словарь по кибернетике. 2-е изд / Под ред. В. С. Михалевича. — Киев: Украинская советская энциклопедия, 1989. — 751 с. — ISBN 5-88500-008-5.
Инвертор
Простейшим логическим элементом является инвертор, который просто изменяет входной сигнал на прямо противоположное
значение. Его логическая функция записывается в следующем виде:
где черта над входным значением и обозначает изменение его на противоположное. То же самое действие можно записать
при помощи , приведённой в таблице 1.
Так как вход у инвертора только один, то его таблица истинности состоит всего из двух строк.
Таблица 1. Таблица истинности логического элемента инвертора
| In | Out |
|---|---|
| 1 | |
| 1 |
В качестве логического инвертора можно использовать простейший усилитель с транзистором, включенном по
схеме с общим эмиттером (или истоком для полевого транзистора).
Принципиальная схема логического элемента инвертора, выполненная на биполярном n-p-n транзисторе, приведена на рисунке 1.
Микросхемы логических инверторов могут обладать различным временем распространения сигнала и могут работать на различные
виды нагрузки. Они могут быть выполнены на одном или на нескольких транзисторах. Наиболее распространены логические элементы,
выполненные по ТТЛ, ЭСЛ и КМОП технологиям. Но независимо от схемы логического
элемента и её параметров все они осуществляют одну и ту же функцию.
Для того, чтобы особенности включения транзисторов не затеняли выполняемую функцию, были введены специальные обозначения
для логических элементов — условно-графические обозначения. инвертора приведено на рисунке 2.
Инверторы присутствуют практически во всех сериях цифровых микросхем. В отечественных микросхемах инверторы обозначаются
буквами ЛН. Например, в микросхеме 1533ЛН1 содержится 6 инверторов. Иностранные микросхемы для обозначения типа микросхемы
используется цифровое обозначение. В качестве примера микросхемы, содержащей инверторы, можно назвать 74ALS04. В названии
микросхемы отражается, что она совместима с ТТЛ микросхемами (74), произведена по улучшеной малопотребляющей шоттки технологии
(ALS), содержит инверторы (04).
В настоящее время чаще применяются микросхемы поверхностного монтажа (SMD микросхемы), в которых содержится по одному
логическому элементу, в частности инвертору. В качестве примера можно назвать микросхему SN74LVC1G04. Микросхема произведена
фирмой Texas Instruments (SN), совместима с ТТЛ микросхемами (74) произведена по низковольтовой КМОП технологии (LVC),
содержит только один логический элемент (1G), им является инвертор (04).
Для исследования инвертирующего логического элемента можно использовать широкодоступные радиоэлектронные элементы. Так,
в качестве генератора входных сигналов можно использовать обычные переключатели или тумблеры. Для исследования таблицы
истинности можно даже применить обычный провод, который будем поочередно подключать к источнику питания и ли общему проводу.
В качестве логического пробника может быть использована низковольтовая лампочка или светодиод, соединенный последовательно
с токоограничивающим резистором. Принципиальная схема исследования логического элемента
инвертора, реализованная с помощью этих простейших радиоэлектронных элементов, приведена на рисунке 3.
Логический вентиль
Логический вентиль – базовый элемент логической схемы, выполняющий элементарную логическую операцию, преобразуется множество входных логических сигналов в выходной логический сигнал.С помощью этих схем можно выполнять любые логические функции, описывающие работу устройств компьютера. Логические выражения являются основой для создания электронных схем. Обычно вентили имеют от двух до восьми входов и один или два выхода.Чтобы представить два логических состояния – «1» и «0» в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Высокий уровень обычно соответствует значению «истина» («1»), а низкий – значению «ложь» («0»).Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию. Это упрощает запись и понимание сложных логических схем.Работу логических элементов описывают с помощью таблиц истинности, знакомых из предыдущей темы.Физической основой различных интегральных микросхем, составляющих основные части компьютера, является сложное логическое выражение.
Схема И (рис. 1) выполняет конъюнкцию двух или нескольких логических значений.Схема ИЛИ реализует дизъюнкцию двух или более логических значений.Схема НЕ (инвертор) реализует операцию отрицания.
Рисунок 1
Рисунок 2
Рисунок 3
Многозначная логика
Операции, называемой в двоичной логике конъюнкция, в многозначных логиках обычно сопоставляется операция минимум: min(a,b){\displaystyle min(a,b)}, где a,b∈{,…,k−1},{\displaystyle a,b\in \{0,\dots ,k-1\},} а k{\displaystyle k} — значность логики; впрочем, возможны и другие варианты обобщения обычной конъюнкции на многозначный случай. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов {\displaystyle 0} и k−1{\displaystyle k-1}.
Название этой операции минимум имеет смысл в логиках с любой значностью, в том числе и в двоичной логике, а названия конъюнкция, логи́ческое «И», логическое умноже́ние и просто «И» характерны для двоичной логики, а при переходе к многозначным логикам используются реже.
Логическая функция «И» (умножение)
Функция логики И утверждает, что два или более события должны происходить вместе и одновременно, чтобы происходило выходное действие. Порядок, в котором происходят эти действия, не имеет значения, поскольку он не влияет на конечный результат. Например, & B = B & . В булевой алгебре функция логики И подчиняется коммутативному закону, который допускает изменение положения любой переменной.
Функция «И» представлена в электронике символом точки или полной остановки ( . ) Таким образом, 2-входное ( АВ ) «И» элемент имеет выходной термин, представленный логическим выражением A.B или просто AB.
Представление функции «И» на схеме
Здесь два переключателя A и B соединены вместе, образуя последовательную цепь. Поэтому в вышеупомянутой цепи оба выключателя A «И» B должны быть замкнуты (логика «1»), чтобы включить лампу. Другими словами, оба переключателя должны быть замкнуты или должны иметь логическую «1», чтобы лампа горела.
Тогда логический элемент этого типа (логический элемент «И» ) создает выход только тогда, когда все его входы истины. В терминах булевой алгебры вывод будет ИСТИНА, только когда все его входы ИСТИНА. В электрическом смысле логическая функция «И» равна последовательной цепи, как показано выше.
Поскольку имеется только два переключателя, каждый с двумя возможными состояниями «открытый» или «закрытый». Определяя логическую «0» как то, когда переключатель разомкнут, и логическую «1», когда переключатель замкнут, существует четыре различных способа или комбинации расположения двух переключателей вместе, как показано в таблице ниже.
Таблица истинности для функции «И»
Логические «И» элементы доступны как стандартные пакеты ic, такие как общие TTL 74LS08 Четырехпозиционные 2-входные положительные элементы «И» (или эквивалент CMOS 4081), TTL 74LS11 Тройные 3-входные положительные элементы «И» или 74LS21 Двойные 4-входные положительные элементы «И». «И» ворота можно также «каскадировать» вместе для создания цепей с более чем 4 входами.
Связь с естественным языком
Часто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как {\displaystyle 0}. При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз «и» может нести дополнительный оттенок «и тогда», «и поэтому», «и потом». Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке «Мэри вышла замуж и родила ребёнка» — не то же самое, что «Мэри родила ребёнка и вышла замуж».
Связь с естественным языком
Часто указывают на сходство между дизъюнкцией и союзом «или» в естественном языке, когда он употребляется в смысле «или то, или то, или оба сразу». В юридических документах часто пишут: «и (или)», иногда «и/или», подразумевая «или то, или то, или оба сразу». Составное утверждение «A и/или B» считается ложным, когда ложны оба утверждения A и B, в противном случае составное утверждение истинно. Это в точности соответствует определению дизъюнкции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как {\displaystyle 0}.
Неоднозначность естественного языка заключается в том, что союз «или» используется в двух значениях: то для обозначения дизъюнкции, то для другой операции — строгой дизъюнкции (исключающего «ИЛИ»).
Обозначения
Наиболее часто встречаются следующие обозначения для операции конъюнкции:
a∧b,a&&b,a&b,a⋅b,aANDb,min(a,b){\displaystyle a\land b,\quad a\And \And b,\quad a\And b,\quad a\cdot b,\quad a\,\,\mathrm {AND} \,\,b,\quad \min(a,b)}
(в случае использования точки, как знака логического умножения, этот знак, как и при обычном умножении в алгебре, может быть опущен: ab{\displaystyle ab}).
При этом обозначение a∧b{\displaystyle a\land b}, рекомендованное стандартом ISO 31-11, наиболее широко распространено в современной математике и математической логике, где оно, впрочем, конкурирует со знаком амперсанда &; последний, появившись ещё в I веке до н. э. как графическое сокращение (лигатура) латинского союза et ‘и’, уже Якобом и Иоганном Бернулли в 1685 году использовался в качестве логической связки (у них он, однако, связывал не высказывания, а понятия). Джордж Буль (а за ним — и другие пионеры систематического применения символического метода к логике: У. С. Джевонс, Э. Шрёдер, П. С. Порецкий) обозначал конъюнкцию знаком ⋅{\displaystyle \cdot } — как обычное умножение. Символ ⋀ (перевёрнутый знак дизъюнкции) в качестве обозначения конъюнкции был предложен Арендом Гейтингом (1930).
Обозначение для конъюнкции было использовано и в раннем языке программирования Алгол 60. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для конъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения и (с возможностью замены последнего на ключевое слово ); в языках Паскаль и Ада используется зарезервированное слово ; в языках C и C++ применяются обозначения для побитовой конъюнкции и для логической конъюнкции).
Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что <1{\displaystyle 0<1}), оказывается, что (a∧b)=min(a,b).{\displaystyle (a\land b)\,=\,\min(a,b).} Таким образом, конъюнкция оказывается частным случаем операции вычисления минимума; это открывает наиболее естественный способ определить операцию конъюнкции в системах многозначной логики (хотя иногда рассматривают и другие способы обобщения конъюнкции — например, такой: (a∧b)=ab(modk){\displaystyle (a\land b)\,=\,ab\;(\operatorname {mod} k)} в случае k-значной логики, в которой множество значений истинности представлено начальным отрезком {,…,k−1}{\displaystyle \{0,\dots ,k-1\}} полугруппы N{\displaystyle \mathbb {N} } натуральных чисел).
Применение логоческих элементов
На современном этапе развития цифровой электроники и микросхемотехники простые логические элементы всё меньше находят своё применение именно как выполняющие простые логические функции. Очень часто вышеописанные логические элементы выполняют функции разрешения/запрещения или смешивания/совпадения сигналов в более сложных цифровых схемах.
Схема разрешения/запрещения
Например, применение логического элемента 2И в качестве управляющего можно описать следующим образом. Один из входов считают управляющим, а второй информационным, тогда при лог. 1 на управляющем входе, сигнал с информационного входа проходит на выход без ограничения, но если на управляющем входе низкий логический уровень, то прохождение сигнала с входа на выход отсутствует. Очень часто логические элементы в таком качестве используют для работы на мультиплексированную или двунаправленную линию.
Точно также в качестве элементов разрешении/запрещения используются и другие элементы И, И-НЕ, ИЛИ, ИЛИ-НЕ. Применение того или иного элемента обуславливается уровнем управляющего сигнала, инверсии (или её отсутствия) входного сигнала. Ниже показаны схемы использования логических элементов в качестве разрешающих/запрещающих прохождение сигнала.
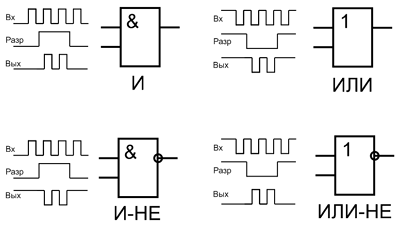
Реализация разрешение/запрещение прохождения сигналов на логических элементах
Схема смешивания сигналов
Довольно часто требуется реализовать смешивание сигналов, когда выходной сигнал должен появляться при приходе сигналов на любой вход логического элемента. Например, использую элемент 2ИЛИ можно реализовать смешивание двух сигналов без инверсии, то есть сигналы, которые приходят на первый и на второй вход, будут отображаться в выходном сигнале. Ниже показаны схемы использования логических элементов в качестве смешивающих с различными уровнями.
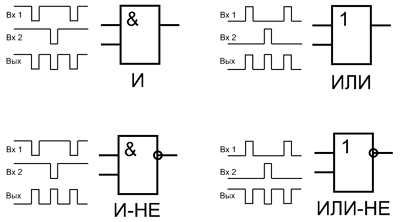
Реализация смешивания сигналов различных логических уровней на логических элементах
Схемы определения совпадения сигналов
На логических элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ очень просто реализовать схемы совпадения входящих сигналов, когда выходной сигнал вырабатывается при совпадении логических уровней входящих сигналов. Ниже показаны схемы совпадения на логических элементах.
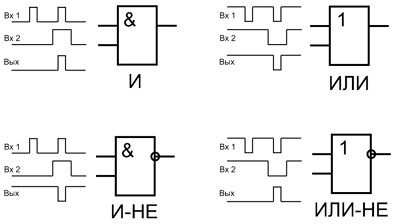
Реализация функции совпадения сигналов на логических элементах
Схемы инвертирования сигналов
Логические элементы И, И-НЕ, ИЛИ, ИЛИ-НЕ, как более сложные по сравнению с элементами НЕ и повторителями, позволяют реализовать функции инверторов и буферных элементов. Для этого просто необходимо соединить их входы или на один из входов подать сигнал соответствующего логического уровня. Ниже показаны схемы повторителей и инверторов на элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ.
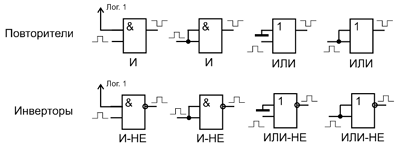
Реализация повторителей и инверторов на логических элементах
Этими простыми схемами не ограничивается применение логических элементов И, И-НЕ, ИЛИ, ИЛИ-НЕ. Больше про применение логических микросхем я обязательно напишу в одном из следующих постов.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
3.1. Что такое алгебра логики
|
Алгебра логики — это раздел математики, изучающий логические переменные, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. |
Алгебра логики возникла в середине ХIХ века в трудах английского математика
Джорджа Буля. Ее создание представляло собой попытку решать традиционные
логические задачи алгебраическими методами.
Совокупность логических переменных х1, …,
хn называется набором переменных.
Логической функцией (функцией алгебры логики) от набора
логических переменных F(х1, …, хn) называется
функция, которая может принимать только два значения: истина или ложь
(1 или 0). Любая логическая функция может быть задана с помощью таблицы
истинности, в левой части которой записываются возможные наборы значений
аргументов, а в правой — соответствующие им значения функции.
Логический элемент «ИЛИ»
Следующим простейшим логическим элементом является схема, реализующая операцию логического сложения «ИЛИ»:
F(x1,x2) = x1Vx2
где символ V обозначает функцию логического сложения. Иногда эта же функция записывается в другом виде:
F(x1,x2) = x1Vx2 = x1+x2 = x1|x2.
То же самое действие можно записать при помощи таблицы истинности, приведённой в таблице 4. В формуле, приведенной выше
использовано два аргумента. Поэтому логический элемент, выполняющий эту функцию имеет два входа. Такой элемент обозначается
«2ИЛИ». Для элемента «2ИЛИ» таблица истинности будет состоять из четырех строк (22 = 4).
Таблица 4. Таблица истинности логического элемента «2ИЛИ»
| In1 | In2 | Out |
|---|---|---|
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 | 1 |
Как и в случае, рассмотренном для , воспользуемся для реализации схемы
«2ИЛИ» ключами. На этот раз соединим ключи параллельно. Схема, реализующая таблицу истинности 4, приведена на
рисунке 5. Как видно из приведённой схемы, уровень логической единицы появится на её выходе, как только будет замкнут
любой из ключей, то есть схема реализует таблицу истинности, приведённую в таблице 4.
Так как функция логического суммирования может быть реализована различными принципиальными схемами,
то для обозначения этой функции на принципиальных схемах используется специальный символ «1», как это приведено на
рисунке 6.
Дата последнего обновления файла
29.03.2018
Логический элемент «И-НЕ»
Показана схема на рис. 5 а. Здесь диод Д3 выполняет роль так сказать фильтра во избежание искажения сигнала. Если на вход х1 или х2 не подан сигнал (х1=0 или х2=0), то через диод Д1 или Д2 будет протекать ток. Падение на нем не равно нулю и может оказаться достаточным для открытия транзистора. Последствием чего может стать ложное срабатывание и на выходе вместо единицы мы получим ноль. А если в цепь включить Д3, то на нем упадет значительная часть напряжения открытого на входе диода, и на базу транзистора практически ничего не приходит. Поэтому он будет закрыт, а на выходе будет единица, что и требуется при наличии нуля на каком либо из входов. На рис. 5б и в показаны таблица истинности и схемное обозначение данного устройства.
 Рис.5
Рис.5
Логические элементы получили широчайшее применение в электронике и микропроцессорной технике. Многие системы управления строятся с использованием именно этих устройств.
Обозначения
Наиболее часто встречаются следующие обозначения для операции дизъюнкции:
- a∨b,a{\displaystyle a\lor b,\;a} || b,a{\displaystyle b,\;a} | b,a ORb{\displaystyle b,\;a~{\mbox{OR}}\,\,b},max(a,b).{\displaystyle ,\;\max(a,b).}
При этом обозначение a∨b{\displaystyle a\lor b}, рекомендованное международным стандартом ISO 31-11, наиболее широко распространено в современной математике и математической логике. Появилось оно не сразу: Джордж Буль, положивший начало систематическому применению символического метода к логике, не работал с дизъюнкцией (используя вместо неё строгую дизъюнкцию, которую обозначал знаком +), а Уильям Джевонс предложил для дизъюнкции знак . Эрнст Шрёдер и П. С. Порецкий вновь использовали знак +, но уже применительно к обычной дизъюнкции. Символ ∨{\displaystyle \lor } как обозначение дизъюнкции впервые встречается в статье «Математическая логика, основанная на теории типов»Бертрана Рассела (1908); он образован от лат. vel, что означает «или».
Обозначение для дизъюнкции было использовано и в раннем языке программирования Алгол 60. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для дизъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения и (с возможностью замены последнего на ключевое слово ); в языках Паскаль и Ада используется зарезервированное слово ; в языках C и C++ применяются обозначения для побитовой дизъюнкции и для логической дизъюнкции).
Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что <1{\displaystyle 0<1}), оказывается, что (a∨b)=max(a,b).{\displaystyle (a\lor b)\,=\,\max(a,b).} Таким образом, дизъюнкция оказывается частным случаем операции вычисления максимума; это открывает наиболее естественный способ определить операцию дизъюнкции в системах многозначной логики.
Логическая функция «НЕ» (отрицание)
Функция «Логическое НЕ» — это просто инвертор с одним входом, который изменяет вход логического уровня «1» на выход логического уровня «0» и наоборот.
«Функция логического НЕ» называется так, потому что ее выходное состояние НЕсовпадает с его входным состоянием с ее логическим выражением, обычно обозначаемым чертой или линией ( ¯ ) над его входным символом, который обозначает операцию инвертирования (отсюда ее название как инвертор).
Поскольку логическое «НЕ» выполняет логическую функцию инвертирования или комплементационной, их чаще называют инверторами, поскольку они инвертируют сигнал. В логических схемах это отрицание может быть представлено нормально замкнутым переключателем.
Представление функции «НЕ» на схеме
Если A означает, что переключатель замкнут, то «НЕ» A или А (с верхней чертой) говорит, что переключатель НЕ замкнут или, другими словами, он разомкнут. Функция логического НЕ имеет один вход и один выход, как показано на рисунке.
Таблица истинности для функции «НЕ»
Индикатор инверсии для логической функции «НЕ» является символом «пузыря», ( O) на выходе (или входе) символа логических элементов. В булевой алгебре инвертирующая логическая функция «НЕ» следует Закону дополнения, создающему инверсию.
Логические «НЕ» элементы или «Инверторы», как их чаще называют, могут быть связаны со стандартными элементами «И» и» ИЛИ» для создания элементов «НЕ И» и «НЕ ИЛИ» соответственно. Инверторы также могут использоваться для генерации «дополнительных» сигналов в более сложных декодерах / логических схемах, например, дополнение логики A — это «НЕ» A , а два последовательно соединенных инвертора дают двойную инверсию, которая выдает на своем выходе исходное значение A.
При проектировании логических схем вам может понадобиться только один или два инвертора в вашей конструкции, но если у вас нет места или денег для выделенного чипа инвертора, такого как 74LS04. Тогда вы можете легко заставить логику «НЕ» функционировать, используя любые запасные элементы «НЕ А» или «НЕ ИЛИ», просто соединяя их входы вместе, как показано ниже.
Примечания
- Гутников В. С. . Интегральная электроника в измерительных приборах. — Л.: Энергия, 1974. — 144 с. — С. 14—16.
- , с. 534.
- Стяжкин Н. И. . Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 320, 349, 352, 368.
- . // Website Jeff Miller Web Pages. Дата обращения 5 февраля 2016.
- , с. 149—150.
- , с. 30.
- Пратт Т. . Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
- Грогоно П. . Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
- Вегнер П. . Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
- Эллис М., Строуструп Б. . Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
- Яблонский С. В. . Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
- Рвачёв В. Л. . Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.