Логические выражения

Джордж Буль

Сама личность автора заслуживает отдельного внимания. Даже учитывая то, что в прошлом люди взрослели раньше нас, все равно нельзя не отметить, что в 16 лет Дж. Буль преподавал в деревенской школе, а к 20 годам открыл собственную школу в Линкольне. Математик отлично владел пятью иностранными языками, а в свободное время зачитывался работами Ньютона и Лагранжа. И все это — о сыне простого рабочего!

В 1839 году Буль впервые послал свои научные работы в Кембриджский математический журнал. Ученому исполнилось 24 года. Работы Буля настолько заинтересовали членов Королевского научного общества, что в 1844 году он получил медаль за вклад в развитие математического анализа. Еще несколько опубликованных работ, в которых были описаны элементы математической логики, позволили молодому математику занять пост профессора в колледже графства Корк. Напомним, что у самого Буля образования не было.

Логические основы работы компьютера

Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых “ложь” и “истина”. Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.

Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если “отсутствует” электрический сигнал, и 1, если “имеется” электрический сигнал.

Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».

Логический элемент «НЕ» (инвертор)

Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.

У этого элемента один вход и один выход. На функциональных схемах он обозначается:

Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.

Проверь соответствие логического элемента “НЕ” логическому элементу “НЕ”. Воспользуйся тренажером Логические элементы.xlsx

Логический элемент «И» (конъюнктор)

Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.

Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:

Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.

Проверь соответствие логического элемента “И” логическому элементу “И”. Воспользуйся тренажером Логические элементы.xlsx

Логический элемент «ИЛИ» (дизъюнктор)

Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:

Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.

На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.

Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.

Проверь соответствие логического элемента “ИЛИ” логическому элементу “ИЛИ”. Воспользуйся тренажером Логические элементы.xlsx

Пример 1. Составьте логическую схему для логического выражения: F=A / B / A.

1. Две переменные – А и В.

2. Две логические операции: 1-/, 2-/.

Пример 2. Постройте логическую схему, соответствующую логическому выражению F=А/В/ ¬(В/А). Вычислить значения выражения для А=1,В=0.

1. Переменных две: А и В; 1 4 3 2

2. Логических операций три: / и две /; А/В/ ¬ (В/ А).

3. Схему строим слева направо в соответствии с порядком логических операций:

4. Вычислим значение выражения: F=1 / 0 / ¬(0 / 1)=0

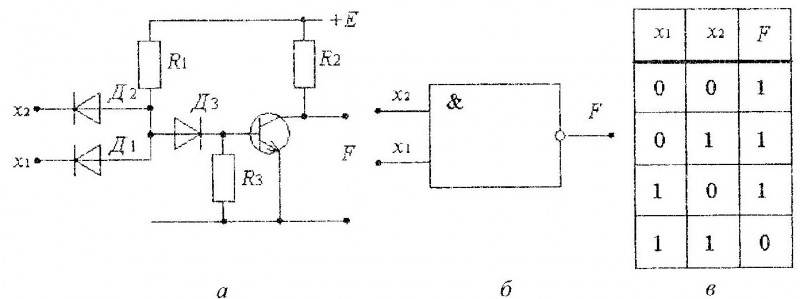
Схемой И у или конъюнктороМу называется такая логическая схема, на выходе которой логическая единица появляется только тогда, когда на всех ее входах имеются логические единицы.

Таблица истинности конъюнктора

Принципиальная схема конъюнктора: диодная сборка

Здесь А и В — входные сигналы. В таблице 6.2 приводится описание работы диодной сборки.

Описание работы конъюнктора

D₂ — закрыт, D, — открыт

Схемой ИЛИ у или дизъюнкторому называется такая логическая схема, на выходе которой логическая единица появляется тогда, когда хотя бы на одном из входов присутствует логическая единица.

Таблица истинности дизъюнктора

Принципиальная схема дизъюнктора

В таблице 6.3 дано описание работы диодной схемы дизъюнктора.

Высказывания

Объектом изучения алгебры логики являются высказывания, которые представляют собой повествовательные предложения, которые могут быть однозначно оценены как истинные или ложные. Истинность высказывания обозначают единицей, ложность – нулем. Примером высказывания может быть предложение «Москва столица Российской федерации». Высказывания принято обозначать латинскими буквами.

Не все предложения, несущие ту или иную информацию можно назвать высказываниями. Например, вопросительные или побудительные предложения – это не высказывания. Также не являются высказываниями математические выражения с переменными.

Например, не являются высказываниями следующие предложения:

• Сколько весит слон?
• Летайте самолетами Аэрофлота!
• 5*х + 8*y = 24
• Этот фильм самый лучший.

Алгебра логики изучает методы работы с высказываниями.

Логические операции. Дизъюнкция, конъюнкция и отрицание

Так как же связываются между собой простые логические высказывания, образуя
сложные? В естественном языке мы используем различные союзы и другие части
речи. Например, «и», «или», «либо», «не», «если», «то», «тогда». Пример сложных
высказываний: «у него есть знания и навыки», «она приедет во
вторник, либо в среду», «я буду играть тогда,
когда сделаю уроки», «5 не равно 6». Как мы решаем, что нам
сказали правду или нет? Как-то логически, даже где-то неосознанно, исходя из
предыдущего жизненного опыта, мы понимает, что правда при союзе «и» наступает в
случае правдивости обоих простых высказываний. Стоит одному стать ложью и все
сложное высказывание будет лживо. А вот, при связке «либо» должно быть правдой
только одно простое высказывание, и тогда все выражение станет истинным.

Булева алгебра переложила этот жизненный опыт на аппарат математики,
формализовала его, ввела жесткие правила получения однозначного результата. Союзы
стали называться здесь логическими операторами.

Алгебра логики предусматривает множество логических операций. Однако три из
них заслуживают особого внимания, т.к. с их помощью можно описать все
остальные, и, следовательно, использовать меньше разнообразных устройств при
конструировании схем. Такими операциями являются конъюнкция
(И), дизъюнкция (ИЛИ) и отрицание (НЕ). Часто
конъюнкцию обозначают &, дизъюнкцию — ||,
а отрицание — чертой над переменной, обозначающей высказывание.

При конъюнкции истина сложного выражения возникает лишь в случае истинности
всех простых выражений, из которых состоит сложное. Во всех остальных случаях
сложное выражение будет ложно.

При дизъюнкции истина сложного выражения наступает при истинности хотя бы
одного входящего в него простого выражения или двух сразу. Бывает, что сложное
выражение состоит более, чем из двух простых. В этом случае достаточно, чтобы
одно простое было истинным и тогда все высказывание будет истинным.

Отрицание – это унарная операция, т.к выполняется по отношению к одному
простому выражению или по отношению к результату сложного. В результате
отрицания получается новое высказывание, противоположное исходному.

Как решать тесты

Математическая логика подразумевает упрощение заданных уравнений. Так же, как и в алгебре, необходимо сначала максимально облегчить условие (избавиться от сложных вводных и операций с ними), а затем приступить к поиску верного ответа.

Что же сделать для упрощения? Преобразовать все производные операции в простые. Затем раскрыть все скобки (или наоборот, вынести за скобки, чтобы сократить этот элемент). Следующим действием должно стать применение свойств булевой алгебры на практике (поглощение, свойства нуля и единицы и т. д).

В конечном итоге уравнение должно состоять из минимального количества неизвестных, объединенных простыми операциями. Легче всего искать решение, если добиться большого количества тесных отрицаний. Тогда ответ всплывет как бы сам собой.

Логические основы компьютера

В ЭВМ используются различные устройства, работу которых прекрасно описывает
алгебра логики. К таким устройствам относятся группы переключателей, триггеры,
сумматоры.

Кроме того, связь между булевой алгеброй и компьютерами лежит и в
используемой в ЭВМ системе счисления. Как известно она двоичная. Поэтому в
устройствах компьютера можно хранить и преобразовывать как числа, так и
значения логических переменных.

Переключательные схемы

В ЭВМ применяются электрические схемы, состоящие из множества
переключателей. Переключатель может находиться только в двух состояниях:
замкнутом и разомкнутом. В первом случае – ток проходит, во втором – нет.
Описывать работу таких схем очень удобно с помощью алгебры логики. В
зависимости от положения переключателей можно получить или не получить сигналы
на выходах.

Вентили, триггеры и сумматоры

Вентиль представляет собой логический элемент, который принимает одни
двоичные значения и выдает другие в зависимости от своей реализации. Так,
например, есть вентили, реализующие логическое умножение (конъюнкцию), сложение
(дизъюнкцию) и отрицание.

Триггеры и сумматоры – это относительно сложные устройства, состоящие из
более простых элементов – вентилей.

Триггер способен хранить один двоичный разряд, за счет того, что может
находиться в двух устойчивых состояниях. В основном триггеры используется в
регистрах процессора.

Сумматоры широко используются в арифметико-логических устройствах (АЛУ)
процессора и выполняют суммирование двоичных разрядов.

Законы алгебры логики

Для
логических величин обычно используются три операции:

1. Конъюнкция – логическое умножение (И) – and,
   &, ∧.
2. Дизъюнкция – логическое сложение (ИЛИ) – or,
   |, v.
3. Логическое отрицание (НЕ) – not,
   ¬.

Логические
выражения можно преобразовывать в соответствии с законами алгебры логики:

1. Законырефлексивности
   a ∨ a = a
   a ∧ a = a
2. Законы коммутативности
   a ∨ b = b ∨ a
   a ∧ b = b ∧ a
3. Законы ассоциативности
   (a ∧ b) ∧ c = a ∧ (b ∧ c)
   (a ∨ b) ∨ c = a ∨ (b ∨ c)
4. Законы дистрибутивности
   a ∧ (b ∨ c) = a ∧ b ∨ a ∧ c
   a ∨ b ∧ c = (a ∨ b) ∧ (a ∨ c)
5. Закон отрицания отрицания
   ¬ (¬ a) = a
6. ЗаконыдеМоргана
   ¬ (a ∧ b) = ¬
   a ∨ ¬ b
   ¬ (a ∨ b) = ¬
   a ∧ ¬ b
7. Законыпоглощения
   a ∨ a ∧ b = a
   a ∧ (a ∨ b) = a

Что такое алгебра логики?

Алгебра логики (булева алгебра) – это раздел математики, возникший в XIX веке благодаря усилиям английского математика Дж. Буля. Поначалу булева алгебра не имела никакого практического значения. Однако уже в XX веке ее положения нашли применение в описании функционирования и разработке различных электронных схем. Законы и аппарат алгебры логики стал использоваться при проектировании различных частей компьютеров (память, процессор). Хотя это не единственная сфера применения данной науки.

Что же собой представляет алгебра логики? Во-первых, она изучает методы установления истинности или ложности сложных логических высказываний с помощью алгебраических методов. Во-вторых, булева алгебра делает это таким образом, что сложное логическое высказывание описывается функцией, результатом вычисления которой может быть либо истина, либо ложь (1, либо 0). При этом аргументы функции (простые высказывания) также могут иметь только два значения: 0, либо 1.

Что такое простое логическое высказывание? Это фразы типа «два больше одного», «5.8 является целым числом». В первом случае мы имеем истину, а во втором ложь. Алгебра логики не касается сути этих высказываний. Если кто-то решит, что высказывание «Земля квадратная» истинно, то алгебра логики это примет как факт. Дело в том, что булева алгебра занимается вычислениями результата сложных логических высказываний на основе заранее известных значений простых высказываний.