Основы логики и логические основы компьютера. логика это наука о формах и способах мышления

Введение в булевую алгебру

В 1854 году Джордж Буль провел исследование «законов мышления», которые основывались на упрощенной версии теории «групп» или «множеств», и из этого была выведена булевая алгебра.

Булева алгебра имеет дело, главным образом, с теорией, согласно которой логические операции и операции над множествами являются либо «ИСТИННЫМИ», либо «ЛОЖНЫМИ», но не обеими одновременно.

Например, A + A = A, а не 2A, как это было бы в обычной алгебре. Булева алгебра — это простой и эффективный способ представления действия переключения стандартных логических вентилей, а основные логические операторы, которые нас здесь интересуют, задаются операциями логических вентилей функций И , ИЛИ и НЕ.

Содержание

• Логические основы работы компьютера

  Слайд 1

  Логика – наука о формах
  и способах мышления.

• Слайд 2

  Понятие –это форма мышления,фиксирующая основные, существенные признаки объекта.

• Слайд 3

  это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинно, либо ложно.

• Слайд 4

  -это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).

• Слайд 5

  Логическое умножение (конъюнкция)
  Логическое сложение (дизъюнкция)
  Логическое отрицание (инверсия)

• Слайд 6

  Составное высказывание, образованное в результате операции логического умножения истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.
  «и», &,

• Слайд 7

• Слайд 8

  Составное высказывание, образованное в результате логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
  «Или», v

• Слайд 9

• Слайд 10

  Делает истинное высказывание ложным и наоборот, ложное — истинным.
  «не», а,

• Слайд 11

• Слайд 12

  Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
  «…тогда и только тогда, когда …»

• Слайд 13

• Слайд 14

  Составное высказывание, образованное с помощью операции логического следования (импликации) ложно тогда и только тогда, когда из истиной предпосылки следует ложный вывод.

• Слайд 15

• Слайд 16

  Логические переменные
  Знаки логических операций

• Слайд 17

  AVB

• Слайд 18

• Слайд 19

  1. Закон тождества
  А=А
  2. Закон непротиворечия А&А=0
  3.Закон исключенного третьего
  AVА=1
  4.Закон двойного отрицания А=А

• Слайд 20

  A&B=AVB

• Слайд 21

  AVB=BVA

• Слайд 22

  (AVB)VC=AV(BVC)

• Слайд 23

  (AVB)&(AVC)=AV(B&C)

• Слайд 24

  1.Напишите таблицу истинности для операции конъюнкция.
  2.Напишите таблицу истинности для операции дизъюнкция.
  3.Напишите таблицу истинности для операции импликация.
  4. Напишите таблицу истинности для операции эквивалентность.

• Слайд 25

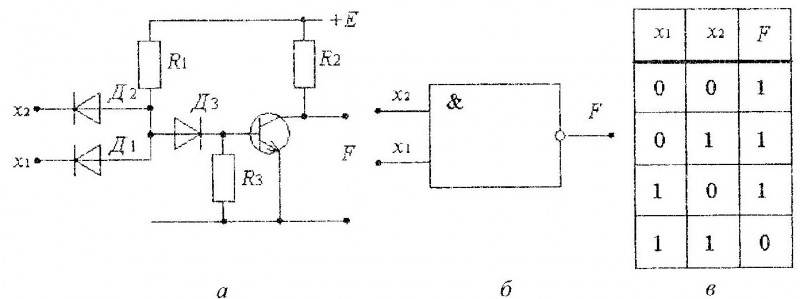
  1.С помощью таблицы истинности получите результат логической функции A&B
  2.Какому логическому элементу соответствует логическая схема:

• Слайд 26

  3.Дана логическая схема. Напишите по ней логическую функцию и составьте таблицу истинности.

  V
  &
  V

  Х
  У
  А

• Слайд 27

• Слайд 28

  5. Для составления цепочек используются бусины A, B,C, D,E. На первом месте в цепочке стоит одна из бусин А, С, Е. На втором – любая гласная, если первая буква согласная и любая согласная, если первая гласная. На третьем месте одна из бусин C,D,E, не стоящая в цепочке на 1-ом месте.Какая из цепочек создана по этому правилу?
  1)СВE 2)ADD 3)ECE 4)EAD

Посмотреть все слайды

3.11. Что такое переключательная схема

В компьютерах и других автоматических устройствах широко применяются
электрические схемы, содержащие сотни и тысячи переключательных элементов: реле,
выключателей и т.п. Разработка таких схем весьма трудоёмкое дело. Оказалось, что
здесь с успехом может быть использован аппарат алгебры логики.

Переключательная схема — это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал.

Каждый переключатель имеет только два состояния: замкнутое и
разомкнутое. Переключателю Х поставим в соответствие логическую
переменную х, которая принимает значение 1 в том и только в том случае,
когда переключатель Х замкнут и схема проводит ток; если же переключатель
разомкнут, то х равен нулю.

Будем считать, что два переключателя Х и связаны
таким образом, что когда Х замкнут, то
разомкнут, и наоборот. Следовательно, если переключателю Х поставлена в
соответствие логическая переменная х, то переключателю должна
соответствовать переменная .

Всей переключательной схеме также можно поставить в соответствие логическую
переменную, равную единице, если схема проводит ток, и равную нулю — если не
проводит. Эта переменная является функцией от переменных, соответствующих всем
переключателям схемы, и называется функцией проводимости.

Найдем функции проводимости F некоторых переключательных схем:

a)  

Схема не содержит переключателей и проводит ток всегда, следовательно
F=1; 

б)  

Схема содержит один постоянно разомкнутый контакт, следовательно
F=0; 

в)  

Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х
разомкнут, следовательно, F(x) = x; 

г)  

Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда
х замкнут, следовательно, F(x) = ; 

д)  

Схема проводит ток, когда оба переключателя замкнуты, следовательно,
F(x) = x . y; 

е)  

Схема проводит ток, когда хотя бы один из переключателей замкнут,
следовательно, F(x)=x v y; 

ж)  

Схема состоит из двух параллельных ветвей и описывается функцией . 

Две схемы называются равносильными, если через одну из них проходит ток тогда и только тогда, когда он проходит через другую (при одном и том же входном сигнале). Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей.

Задача нахождения среди равносильных схем наиболее простых является очень
важной. Большой вклад в ее решение внесли российские учёные Ю.И

Журавлев,
С.В. Яблонский и др.

При рассмотрении переключательных схем возникают две основные задачи:
синтез и анализ схемы.

СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим трём
этапам:

1. составлению функции проводимости по таблице истинности, отражающей эти
   условия;
2. упрощению этой функции;
3. построению соответствующей схемы.

АНАЛИЗ СХЕМЫ сводится к

1. определению значений её функции проводимости при всех возможных наборах
   входящих в эту функцию переменных.
2. получению упрощённой формулы.

Примеры.

1. Построим схему, содержащую 4 переключателя
x, y, z и t, такую, чтобы она проводила ток тогда и только тогда, когда замкнут
контакт переключателя t и какой-нибудь из остальных трёх контактов.

Решение. В этом случае можно обойтись без построения таблицы
истинности. Очевидно, что функция проводимости имеет вид F(x, y, z, t) =
t . (x v y v z), а схема выглядит так:

2. Построим схему с пятью переключателями,
которая проводит ток в том и только в том случае, когда замкнуты ровно четыре из
этих переключателей.

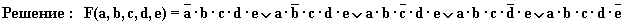
Схема имеет вид:

3. Найдем функцию проводимости схемы:

Решение. Имеется четыре возможных пути прохождения тока при замкнутых
переключателях a, b, c, d, e : через переключатели a, b; через переключатели a,
e, d; через переключатели c, d и через переключатели c, e, b. Функция
проводимости F(a, b, c, d, e) = a . b   v   a .
e . d   v   c . d   v   c .
e . b.

4. Упростим переключательные схемы:

а)  

Решение:   

Упрощенная схема:

б)  

.

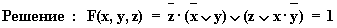Здесь первое логическое слагаемое является
отрицанием второго логического слагаемого , а
дизъюнкция переменной с ее инверсией равна 1.

Упрощенная схема :

в)  

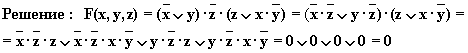
Упрощенная схема:

г)  

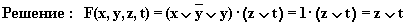
Упрощенная схема:

д)  

(по
закону склеивания)

Упрощенная схема:

е)  

Решение: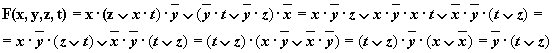

Упрощенная схема:

Расширенные и редко используемые символы

Символы отсортированы согласно коду Unicode:

• U+00B7 • Точка в середине, устаревший способ обозначения AND, остаётся употребимым в электронике, например, «A•B» означает то же самое, что и «A&B»
• • : Центральная точка с чертой над ней, устаревший способ для обозначения И-НЕ, например, «A•B» означает то же, что и «A И-НЕ B», или «A|B», или «¬(A & B)». См. также символ Unicode U+22C5 ⋅ оператор точка.

• U+0305 ◌̅ Комбинируемое надчёркивание, используется для сокращения стандартных представлений чисел (). Например, «4̅» является сокращённым написанием стандартного числа «SSSS0».
• Надчёркивание также иногда используется для обозначения нумерации Гёделя, например, «AVB» обозначает номер Гёделя для «(AVB)»
• Надчёркивание также является устаревшим способом обозначения отрицания, но продолжает использоваться в электронике, например, «AVB» означает то же самое, что и «¬(AVB)»

• U+2191 ↑ Стрелка вверх или U+007C | Вертикальная черта: Штрих Шеффера, знак для оператора И-НЕ.
• U+2201 ∁ Дополнение
• U+2204 ∄ Не существует: перечёркнутый квантор существования, то же самое, что и «¬∃»
• U+2234 ∴
• U+2235 ∵
• U+22A7 ⊧ Импликация (логическое следование): является моделью для …. Например, A ⊧ B означает, что из A следует B. В любой модели, где A ⊧ B, если А верно, то и B верно.
• U+22A8 ⊨ Истина: является истиной.
• U+22AC ⊬ Невыводимо: отрицание ⊢, символ невыводимо, например, T ⊬ P означает, что «P не является теоремой в T»
• U+22AD ⊭ Неверно: не является истиной
• U+22BC ⊼ НЕ-И: другой оператор НЕ-И, может быть записан также как ∧
• U+22BD ⊽ ИЛИ-НЕ: оператор Исключающее ИЛИ, может быть записан также как V
• U+22C4 ⋄ Ромб: модальный оператор для «возможно, что», «не обязательно нет» или, редко, «непротиворечиво» (в большинстве модальных логик оператор определяется как «¬¬»)
• U+22C6 ⋆ Звёздочка: обычно используется как специальный оператор
• U+22A5 ⊥ Кнопка вверх или U+2193 ↓ Стрелка вниз: стрелка Пирса, символ исключающего ИЛИ. Иногда «⊥» используется для противоречия или абсурда.

U+2310 ⌐ Отменённый НЕ

U+231C ⌜ Левый верхний уголок и U+231D ⌝ Правый верхний уголок: угловые скобки, также называемые «кавычками Куайна». Используется как квазикавычки, то есть выделение определённого контекста неопределённого выражения («переменной»). Используется также для чисел Гёделя. Например, «⌜G⌝» обозначает число Гёделя для G. (Типографическое замечание: хотя кавычки появляются всегда в «паре» в (231C и 231D в Unicode), они не всегда симметричны в некоторых фонтах, а в некоторых фонтах, таких как Arial, они симметричны только при определённых размерах букв). Альтернативно кавычки могут быть представлены как ⌈ и ⌉ (U+2308 и U+2309) или с помощью символов отрицания и обратного отрицания ⌐ ¬ в верхнем индексе.)

U+25FB Средний белый квадрат или U+25A1 □ Белый квадрат: модальный оператор необходимо, чтобы (в модальной логике), или доказуемо (в логике доказуемости), или обязательно (в нормативной логике), или убеждены, что (в доксастической логике).

Следующие операторы редко поддерживаются стандартными фонтами. Если вы хотите использовать их на своей странице, вам следует всегда встраивать нужные фонты, чтобы браузер мог отражать символы без необходимости устанавливать фонты на компьютер.

• U+27E1 ⟡ Незакрашенный ромб с вогнутыми сторонами
• U+27E2 ⟢ Незакрашенный ромб с вогнутыми сторонами и чёрточкой влево: модальный оператор для никогда не было
• U+27E3 ⟣ Незакрашенный ромб с вогнутыми сторонами и чёрточкой вправо: модальный оператор для никогда не будет
• U+27E4 ⟤ Незакрашенный квадрат с чёрточкой влево: модальный оператор для всегда было
• U+27E5 ⟥ Незакрашенный квадрат с чёрточкой вправо: модальный оператор для всегда будет

Польша и Германия

В Польше квантор всеобщности иногда записывается как ∧{\displaystyle \wedge }, а квантор существования как ∨{\displaystyle \vee }.
То же самое наблюдается в немецкой литературе.

Минимизация булевых функций

В данном сервисе для минимизации булевых функций используются метод Квайна и карт Карно-Вейча. После получения минимальной формы имеется возможность заново построить логическую схему. Если исходная схема понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить).

1. Kx v K ≡ K — тождество поглощения;
2. Kx v Kx ≡ K — тождество склеивания;
3. Kx v Ky ≡ K(xvy) — дистрибутивный закон,

K_iii_i

Метод карт Карно

Операции►
Удалить

Операции

• Сохранить как docx
• Сохранить как png

Количество переменныхСетка

После минимизации можно получить логическую схему функции и построить таблицу истинности (кнопка Далее)
Далее

Этот метод используется для БФ не более, чем с шестью аргументами и основан на тождестве склеивания: Kx v Kx ≡ K — две элементарные конъюнкции (ЭК) склеиваются, если они отличаются только знаком инверсии одного аргумента. Чтобы облегчить нахождение таких пар (четверок, восьмерок,…) склеивающихся ЭК, используют специальное представление БФ в виде таблицы – карты Карно (другое название — диаграмма Вейча). Чтобы заполнить карту Карно необходимо щелкнуть левой мышкой на соответствующую ячейку.
Карта Карно обладает той особенностью, что две ПЭК, соответствующие соседним клеткам карты, отличаются знаком инверсии только одного аргумента, т.е. их можно склеивать. Причем соседними являются не только клетки, например, с номерами 1 и 3, но и клетки с номерами 12 и 8, 12 и 4, т.е. карту можно «сворачивать» в цилиндр, соединяя горизонтальные (вертикальные) ее границы.
Две единицы «склеиваются» каждый раз, когда они стоят рядом в строке или столбце (карту можно свернуть в цилиндр). В результате склеивания число букв, входящих в ПЭК, уменьшается на единицу.

Классификация

Мыслительный процесс классифицируется зависимо от разных факторов. Они появлялись на протяжении развития психологической науки под влиянием различных отраслей, учений, теорий.

Виды

Мышление можно разделить на две больших группы: теоретическое и практическое. К первым относится абстрактное мышление, которые часто называют словесно-логическим. Оно строится на суждениях, понятиях. Субъект сравнивает предметы, ситуации, явления, анализирует их, основываясь не только на собственном суждении, но и на мнении окружающих. Это возможно только в том случае, если человек в идеале владеет речью, имеет обширный запас знаний, навыков, умений.

Практические виды мышления в психологии:

1. Образное. Строится на восприятии, представлениях. Такие мыслительные процессы свойственны архитекторам, художникам, парфюмерам, модельерам, поэтам. Они начинают проявляться уже в школьном возрасте. Некоторые образные мыслительные процессы наблюдаются в поведении высших животных.
2. Наглядно-действенное. Проявляется во внешних действиях. Такие мыслительные процессы строятся на преобразовании сложившейся ситуации для решения насущных проблем.

Теории

Существует несколько теорий мыслительных процессов, которые имеют как сильные, так и слабые стороны:

1. Ассоцианистская — строится на одноименной философской теории. Ее цель в том, чтобы сделать ум проще, сократив его до совокупности элементарных идей, ощущений. Чтобы связать между собой идеи, события, используются ассоциации. Главный недостаток этой теории в том, что с ее помощью невозможно решить проблематику творческого мышления. Из-за этого творческое начало считалось врожденным, а не приобретенным.
2. Бихевиористская. Последователи этой теории утверждают, что мышление — одна из форм приспособления к новым условиям. Бихевиористы подвергались критике исследователей других направлений психологической науки, поскольку учитывали только наблюдаемое поведение, отвергая то, что скрыто от глаз.
3. Теория гештальта. Последователи этой теории критиковали понятие, по которому утверждалось что разум — пассивная совокупность примитивных идей, которые объединяют ассоциациями. Они изучали проблемы психологии мысли, описывая их со стороны восприятия. Проведя несколько практических экспериментов, последователи этой теории предоставили явные различия между непродуктивным и продуктивным мыслительным процессом.
4. Периферическая теория. Ее последователи занимались изучением периферической нервной системы. Согласно теории, человеческий мозг — одна из составляющих частей процесса мышления. При восприятии новой информации задействуется психика, тело, мозг.
5. Психоаналитическая теория. Известнейшее учение Зигмунда Фрейда затронуло изучение мышления. Ученый утверждал, что после рождения, проявляются нарциссические мыслительные процессы, которые постепенно превращаются в объективные.

Также можно выделить когнитивную теорию развития, которая была основана Жаном Пиаже. Ученый утверждал, что проявление мышления зависит от биологических процессов адаптации.

Формы

Существует несколько форм мышления:

1. Суждение — форма, с помощью которой описывается взаимосвязь между явлениями, предметами. Помимо этого, может происходит отрицание.
2. Умозаключение — форма, позволяющая делать различные выводы, которые строятся на ряде суждений. Умозаключения бывают дедуктивными, индуктивными.
3. Понятие — еще одна форма мышления, с помощью которой отражаются существенные отношения, связи, свойства явлений, предметов.

При этом умозаключение относится к высшей форме проявления мыслительных процессов.

Уровни

Разделение мыслительных процессов на отдельные уровни обязано одному из основоположников когнитивной психологии — Аарону Беку. Уровни:

1. Произвольные мысли — считаются поверхностными, контролируемыми, осознаваемыми.
2. Автоматические — к ним относятся стереотипы, которые навязываются человеку в процессе воспитания.
3. Когнитивные убеждения, базовые схемы. Это глубинные мыслительные процессы. Они возникают в области бессознательного, из-за чего сложнее всего изменяются под влиянием внешних факторов.

Закон достаточного основания

Закон достаточного основания утверждает, что любая мысль, для того чтобы иметь силу, обязательно должна быть обоснована какими-либо аргументами (основаниями).

Причем эти аргументы должны быть достаточными для доказательства исходной мысли, т. е. она должна вытекать из них с необходимостью (тезис должен с необходимостью следовать из оснований).

Рассмотрим следующее рассуждение:

На улице сильный гололед (тезис), ведь машины не ездят (основание).

В данном случае логический закон достаточного основания нарушен, так как тезис не вытекает из основания. То есть, того факта, что машины не ездят, вовсе недостаточно, чтобы утверждать, что это происходит по причине гололеда (так как это может быть и по многим другим причинам).

Или еще одно рассуждение:

Преступление совершил Петров (тезис), так как он сам признался в этом (основание).

Здесь также логический закон достаточного основания нарушен, потому что из того, что человек признался в совершении преступления, вовсе не следует, что он действительно его совершил. Ведь признаться под пытками или любым другим давлением можно в чем угодно.

Интересен факт, что именно на законе достаточного основания базируется важный юридический принцип презумпции невиновности, который предписывает считать человека невиновным, даже если он дает показания против себя, до тех пор, пока его вина не будет доказана.

Ну что же, друзья, теперь вы знакомы с кратким курсом формальной логики, и можете смело оперировать описанными инструментами.

В общем-то, теперь самое время пройти тест на логику (о котором мы говорили вначале), чтобы узнать, насколько хорошо вы владеете логическим мышлением.

Понравился пост? Нажми любую кнопку:

Исторический очерк

Впервые вопросы изучения мышления возникли в античные времена. Ученые, философы того времени изучали мыслительные процессы с точки зрения логики, философии. Наиболее выдающимися исследователями античной эпохи, которые внесли большой вклад в изучение были: Алкмеон Кротонский, Пифагор, Гиппократ, Аристотель, Эпикур, Протагор.

Во времена Средневековья значимых открытий не было. Активное изучение началось только с 17 века. При этом мышление считалось врожденной способностью, которое рассматривалось единолично, без влияния психики. Учение, которое значительно повлияло на изучение мыслительных процессов — прагматизм. Появилось оно в конце 19 века. В 20 веке углубленными исследованиями начали заниматься последователи Вюрцбургской школы. Практические эксперименты этой школы были направлены на то, чтобы разделить мышление на отдельные этапы.

Гештальтпсихология занималась изучением продуктивного мышления. Одновременно исследованиями занимались последователи бихевиоризма. Они изучали навыков, умений, которые использовались людьми для решения различных задач.

Суть и понятие

Мышление — познание мира, осуществляющееся косвенным путем. Его можно назвать познавательной деятельностью, с помощью которой индивид может не ограничивать свои мысли, поступки материальным миром. Ему можно не придерживаться определенных рамок, которые возникают при визуализации объектов. Результаты активности проявляются в поступках, идеях, высказываниях.

Особенности мышления:

• этот процесс позволяет проводить творческую обработку представлений об окружающем мире;
• отражение окружающего мира, различных явлений посредственно;
• способность видеть как отдельные явления, предметы, так и связи, устанавливающиеся между ними.

Опосредованное познание возникает:

1. Когда человеку не нужно покидать дом, чтобы узнать какая погода на улице, идет дождь или светит солнце.
2. Если непосредственное сознание не может дать результатов. Это проявляется в результате влияния рентгеновских, инфракрасных, ультразвуковых лучей.
3. Когда непосредственное сознание не помогает получить информацию из-за временных рамок. Это проявляется при археологических раскопках.
4. При желании расширить границы познания.
5. Активно проявляется при возникновении конфликтов.

Тест по теме: «Основы логики» Наука, изучающая законы и формы мышления, называется

Наука, изучающая законы и формы мышления, называется:

А) алгебра; В) философия;

Б) геометрия; Г) логика.

Повествовательное предложение, в котором что-то утверждается или отрицается, называется:

А) выражение; В) высказывание;

Б) вопрос; Г) умозаключение.

Константа, которая обозначается «1» в алгебре логики называется:А) ложь; В) правда;

Б) истина; Г) неправда.

Какое из следующих высказываний являются истинными? А) город Париж — столица Англии; В) II + VI = VIII;

Б) 3+5=2+4; Г) томатный сок вреден.

Объединение двух высказываний в одно с помощью союза «и» называ­ется:

А) инверсия; В) дизъюнкция;

Б) конъюнкция; Г) импликация.

Чему равно значение логического выражения (l v l) & (l v 0)? А)1; В) 10;

Какая из логических операций не является базовой? А) конъюнкция; В) инверсия;

Б) дизъюнкция; Г) эквивалентность.

Графическое изображение логического выражения называется: А) схема; В) чертеж;

Б) рисунок; Г) график.

Двойное отрицание логической переменной равно:

А) 0; В) исходной переменной;

Б) 1; Г) обратной переменной.

Что такое логика?

A) это наука о суждениях и рассуждениях;

Б) это наука, изучающая законы и методы накопления, обработки и сохранения информации с помощью ЭВМ;

B) это наука о формах и законах человеческого мышления и, в частнос­ти, о законах доказательных рассуждений;

Г) это наука, занимающая изучением логических основ работы компью­тера.

Логическая функция — это:

А) простое высказывание; В) вопросительное предложение;

Б) составное высказывание; Г) логическая операция.

Как кодируется логическая переменная, принимающая значение «ЛОЖЬ»?

Чему равно значение логического выражения (l v l) & (0 v 0)? А)0; В) 10;

Значение логического выражения ¬ (A v B) по закону де Моргана равно: А) ¬А & ¬В; В) ¬А & В;

Логической операцией не является:

А) логическое деление; Б) логическое сложение;

В) логическое умножение; Г) логическое отрицание.

Объединение двух высказываний в одно с помощью оборота «если. то. » называется:

А) инверсия; В) дизъюнкция;

Б) конъюнкция; Г) импликация.

Таблица, содержащая все возможные значения логического выражения, называется:

А) таблица ложности; Б) таблица истинности;

В) таблица значений; Г) таблица ответов.

На один вход приведенной логической схемы подается сиг­нал А, который может принимать значения «1» (истина) или «О» (ложь), на другой — «О» (ложь).

refdb.ru