Закон больших чисел

Доказательство слабого закона

Рассмотрим бесконечную последовательность X1,X2,…{\displaystyle X_{1},X_{2},…} независимых и одинаково распределенных случайных величин с конечным математическим ожиданием E(X1)=E(X2)=…=μ<∞{\displaystyle \mathbb {E} (X_{1})=\mathbb {E} (X_{2})=\ldots =\mu <\infty }, нас интересует сходимость по вероятности

X¯n=1n(X1+⋯+Xn).{\displaystyle {\overline {X}}_{n}={\tfrac {1}{n}}(X_{1}+\cdots +X_{n}).}

Теорема: X¯n →P μ{\displaystyle {\overline {X}}_{n}\ {\xrightarrow {P}}\ \mu }, при n→∞{\displaystyle n\rightarrow \infty }

Предположение о конечной дисперсии D(X1)=D(X2)=…=σ2<∞{\displaystyle D(X_{1})=D(X_{2})=\ldots =\sigma ^{2}<\infty } не является обязательным. Большая или бесконечная дисперсия замедляет сходимость, но ЗБЧ выполняется в любом случае.

Это доказательство использует предположение о конечной дисперсии D⁡(Xi)=σ2{\displaystyle \operatorname {D} (X_{i})=\sigma ^{2}} (для всех i{\displaystyle i}). Независимость случайных величин не предполагает корреляции между ними, мы имеем

D⁡(X¯n)=D⁡(1n(X1+⋯+Xn))=1n2D⁡(X1+⋯+Xn)=nσ2n2=σ2n.{\displaystyle \operatorname {D} ({\overline {X}}_{n})=\operatorname {D} ({\tfrac {1}{n}}(X_{1}+\cdots +X_{n}))={\frac {1}{n^{2}}}\operatorname {D} (X_{1}+\cdots +X_{n})={\frac {n\sigma ^{2}}{n^{2}}}={\frac {\sigma ^{2}}{n}}.}

Математическое ожидание последовательности μ{\displaystyle \mu } представляет собой среднее значение выборочного среднего:

E(X¯n)=μ.{\displaystyle \mathbb {E} ({\overline {X}}_{n})=\mu .}

Используя неравенство Чебышёва для X¯n{\displaystyle {\overline {X}}_{n}}, получаем

P⁡(|X¯n−μ|⩾ε)⩽σ2nε2.{\displaystyle \operatorname {P} (\left|{\overline {X}}_{n}-\mu \right|\geqslant \varepsilon )\leqslant {\frac {\sigma ^{2}}{n\varepsilon ^{2}}}.}

Это неравенство используем для получения следующего:

P⁡(|X¯n−μ|<ε)=1−P⁡(|X¯n−μ|⩾ε)⩾1−σ2nε2,{\displaystyle \operatorname {P} (\left|{\overline {X}}_{n}-\mu \right|<\varepsilon )=1-\operatorname {P} (\left|{\overline {X}}_{n}-\mu \right|\geqslant \varepsilon )\geqslant 1-{\frac {\sigma ^{2}}{n\varepsilon ^{2}}},}

при n→∞{\displaystyle n\rightarrow \infty }, выражение стремится к 1{\displaystyle {\mathit {1}}},

теперь по определению сходимости по вероятности мы получим:

X¯n →P μ{\displaystyle {\overline {X}}_{n}\ {\xrightarrow {P}}\ \mu }, при n→∞{\displaystyle n\rightarrow \infty }.

Доказательство с использованием сходимости характеристических функций

По теореме Тейлора для комплексных функций, характеристическая функция любой случайной величины X{\displaystyle X} с конечным средним μ{\displaystyle \mu } может быть записана как

φX(t)=1+itμ+o(t),t→{\displaystyle \varphi _{X}(t)=1+it\mu +o(t),\quad t\rightarrow 0.}

Все X1,X2,…{\displaystyle X_{1},X_{2},…} имеют одну и ту же характеристическую функцию, обозначим её как φX{\displaystyle \varphi _{X}}.

Среди основных свойств характеристических функций выделим два свойства

φ1nX(t)=φX(tn){\displaystyle \varphi _{{\frac {1}{n}}X}(t)=\varphi _{X}({\tfrac {t}{n}})} и φX+Y(t)=φX(t)φY(t){\displaystyle \varphi _{X+Y}(t)=\varphi _{X}(t)\varphi _{Y}(t)}, X{\displaystyle X} и Y{\displaystyle Y}независимы

Эти правила могут быть использованы для вычисления характеристической функции X¯n{\displaystyle {\overline {X}}_{n}} в терминах φX{\displaystyle \varphi _{X}}

φX¯n(t)=φX(tn)n=1+iμtn+o(tn)n→eitμ,{\displaystyle \varphi _{{\overline {X}}_{n}}(t)=\left^{n}=\left^{n}\,\rightarrow \,e^{it\mu },} при n→∞.{\displaystyle n\rightarrow \infty .}

Предел eitμ{\displaystyle e^{it\mu }}является характеристической функцией константы μ{\displaystyle \mu } и, следовательно, по теореме непрерывности Леви, X¯n{\displaystyle {\overline {X}}_{n}}сходится по распределению к μ{\displaystyle \mu }:

X¯n→Dμ{\displaystyle {\overline {X}}_{n}\,{\xrightarrow {\mathcal {D}}}\,\mu }, при n→∞.{\displaystyle n\to \infty .}

Поскольку μ{\displaystyle \mu }- константа, то отсюда следует, что сходимость по распределению к μ{\displaystyle \mu } и сходимость по вероятности к μ{\displaystyle \mu } эквивалентны. Поэтому,

X¯n→Pμ{\displaystyle {\overline {X}}_{n}\,{\xrightarrow {\mathcal {P}}}\,\mu }, при n→∞.{\displaystyle n\to \infty .}

Это показывает, что среднее значение выборки по вероятности сходится к производной характеристической функции в начале координат, если она существует.

Куда лететь в отпуск и встречу ли я динозавра?

Структура общего решения линейного неоднородного дифференциального уравнения (ДУ). Метод Лагранжа. Метод Лагранжа (Метод вариации произвольных постоянных(МВПП)). 2) Согласно методу вариации произвольных постоянных (Лагранжа), решение уравнения (1) отыскивается в виде (3), в котором и — новые неизвестные функции. Сходимость называется сходимостью последовательности функции распределения к функции распределения или слабой сходимостью последовательности СВ к СВ : для слабой сходимости. Статистические гипотезы относительно неизвестных значений параметров распределения называют параметрическими, все другие гипотезы называются непараметрическими.

И в заключение известный вопрос о вероятности встретить на улице динозавра. Вы за жизнь провели 10 тысяч экспериментов – выходили на улицу и динозавра не встретили. Вероятность встретить динозавра, следовательно, близка к нулю, и нет особых оснований предполагать, что сегодня, выйдя на улицу в 10001 раз, вы его встретите.

Решение.Пусть случайная величинаX– срок службы мотора. Бернулли без доказательства.

Если первый раз герб выпадет при r-ом подбрасывании, r = 1, 2,…, m, игрок получает за партию 2r рублей. Согласно теореме 2, т.е. То есть почти всегда прибыль организаторов игры при взносе А=m мало отличается от нуля (в ту и другую сторону), если число сыгранных партий n велико. Этот результат не зависит от того, постоянно число подбрасываний m в каждой партии или может меняться по желанию игроков.

Рассмотрим пример: пусть вероятность поступления заказа в магазин А равна 0,2 или каждый 5-й звонящий делает заказ. Составим закон распределения поступления 5-ти заказов. Из графика (рис.2) можно увидеть, что вероятность поступления 3-х заказов составляет чуть больше 0,05, а 4-х и 5-ти — очень низкая. Числа 3, 4, 5 будут выпадать очень редко. Число 5 — практически невозможное событие.

Результат каждого опыта в отдельности случаен и непредсказуем, Так средний результат подчиняется закономерностям и предсказуем. Пусть Х — число «успехов» в схеме Бернулли с испытаниями, р — вероятность “успеха” в одном испытании. Он используется в тех случаях, когда неприменима схема случаев, т.е. нам неизвестна симметрия задачи.

Предположим, что в городе Н. предстоят выборы мэра, и число избирателей равно 100 тысячам. Более точным предсказание результата окажется при случайном отборе 1000 человек, и т.д.

Как и любой математический закон, закон больших чисел может быть применим к реальному миру только при известных допущениях, которые могут выполняться лишь с некоторой степенью точности. Так, например, условия последовательных испытаний часто не могут сохраняться бесконечно долго и с абсолютной точностью.

Он же впервые употребил термин «закон больших чисел». Теорему примем без доказательства. Маркову и крупным советским ученым С. Н. Бернштейну и А. Я. Хинчину.

Аналитическая теория чисел

Основная статья: Аналитическая теория чисел

В аналитической теории чисел для вывода и доказательства утверждений о числах и числовых функциях используется мощный аппарат математического анализа (как вещественного, так и комплексного), иногда также теория дифференциальных уравнений. Это позволило значительно расширить тематику исследований теории чисел. В частности, в неё вошли следующие новые разделы:

• Распределение простых чисел в натуральном ряду и в других последовательностях (например, среди значений заданного многочлена).
• Представление натуральных чисел в виде сумм слагаемых определённого вида (простых чисел, квадратов и т . д.).
• Диофантовы приближения.

Первым шагом в применении аналитических методов в теории чисел стал метод производящих функций, сформулированный Эйлером. Для определения количества целочисленных неотрицательных решений линейного уравнения вида

a1x1+…+anxn=N,{\displaystyle a_{1}x_{1}+…+a_{n}x_{n}=N,} где a1,…,an{\displaystyle a_{1},…,a_{n}} — натуральные числа,

Эйлер построил производящую функцию, которая определяется как произведение сходящихся рядов (при |z|<1{\displaystyle |z|<1})

Fi(z)=∑k=∞ziak{\displaystyle F_{i}(z)=\sum _{k=0}^{\infty }{z_{i}^{a}k}}

и является суммой членов геометрической прогрессии, при этом

F(z)=∑N=∞l(N)zN,{\displaystyle F(z)=\sum _{N=0}^{\infty }l(N)z^{N},}

где l(N){\displaystyle l(N)} — число решений изучаемого уравнения.
На основе этого метода был построен круговой метод Харди — Литлвуда.

В работе над квадратичным законом взаимности Гаусс рассмотрел конечные суммы вида

S(a)=∑n=1pe2πian2p,{\displaystyle S(a)=\sum _{n=1}^{p}e^{2\pi ian^{2}/p},}

которые могут быть представлены в виде суммы синусов и косинусов (по формуле Эйлера), из-за чего они являются частным случаем тригонометрических сумм. Метод тригонометрических сумм, позволяющий оценивать число решений тех или иных уравнений или систем уравнений в целых числах, играет большую роль в аналитической теории чисел. Основы метода разработал и впервые применил к задачам теории чисел И. М. Виноградов.

Работая над доказательством теоремы Евклида о бесконечности простых чисел, Эйлер рассмотрел произведение по всем простым числам и сформулировал тождество:

Πp(1−1ps)−1=∑n=1∞1ns,{\displaystyle \Pi _{p}\left(1-{\frac {1}{p^{s}}}\right)^{-1}=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}},}

которое стало основанием для теорий дзета-функций. Наиболее известной и до сих пор не решённой проблемой аналитической теории чисел является доказательство гипотезы Римана о нулях дзета-функции, утверждающей, что все нетривиальные корни уравнения ζ(s)={\displaystyle \zeta (s)=0} лежат на так называемой критической прямой Res=12{\displaystyle \mathrm {Re} \,s={\frac {1}{2}}}, где ζ(s){\displaystyle \zeta (s)} — дзета-функция Римана.

Для доказательства теоремы о бесконечности простых чисел в общем виде Дирихле использовал произведения по всем простым числам, аналогичные эйлерову произведению, и показал, что

Πp(1−χ(p)ps)−1=∑n=1∞χ(n)ns{\displaystyle \Pi _{p}\left(1-{\frac {\chi (p)}{p^{s}}}\right)^{-1}=\sum _{n=1}^{\infty }{\frac {\chi (n)}{n^{s}}}},

при этом функция χ(p){\displaystyle \chi (p)}, получившая название характер Дирихле, определена так, что удовлетворяет следующим условиям: она является периодической, вполне мультипликативной и не равна тождественно нулю. Характеры и ряды Дирихле нашли применение и в других разделах математики, в частности, в алгебре, топологии и теории функций.

Чебышёв показал, что число простых чисел, не превосходящих X{\displaystyle X}, обозначенное как π(X){\displaystyle \pi (X)}, стремится к бесконечности по следующему закону:

aXln⁡(X)<π(X)<bXln⁡(X),{\displaystyle a{\frac {X}{\ln(X)}}<\pi (X)<b{\frac {X}{\ln(X)}},}

где a>12ln⁡2{\displaystyle a>1/2\ln 2} и b<2ln⁡2{\displaystyle b<2\ln 2}.

Применение комплексного анализа позволило значительно углубить наши знания о распределении простых чисел.

Объяснение для того, кто всё же не понял

Бросая монету в игре «орёл или решка» вы вправе ожидать равного числа выпадений любой стороны монеты. Если вдруг монета пять раз подряд выпала «решкой» — о чём это говорит? Или если одна команда обыгрывает равную ей по силе уже пять сезонов подряд – что в этом результате?

Ровным счётом ничего. У монеты нет памяти, которая подсказала бы ей, что решка была в последнее время в фаворе. А состав любой команды за несколько лет может обновиться более чем наполовину. Перед каждым событием вероятность того или иного исхода никак не зависит от предыдущего. Естественно, с точки зрения математики. Вероятность – хорошо видимая на небе звезда, по ней можно ориентироваться в сумрачном мире беттинга, но расстояние до неё слишком велико, чтобы дотянуться или рассмотреть поближе.

Это важно повторить. События в своей последовательности никак не влияют друг на друга, но если их становится много, противоположные исходы стараются разойтись равными группами по разным сторонам

Притом, если у монеты есть два абсолютно равных между собой исхода, то для статистики встречи равных команд перекос всё же имеется, пусть и незначительный. Да и не стоит забывать про возможность ничьи.

Литература

Классические труды

• Charles de la Vallée Poussin. Recherces analytiques sur la théorie des nombres premiers. Ann. Soc. Sci. Bruxells, 1897.
• Чебышёв П. Л. Об определении числа простых чисел, меньших данной величины, 1848.
• Чебышёв П. Л. О простых числах, 1850.

Современная литература

• Дербишир, Джон. Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. — Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2.
• Erdős, P. Démonstration élémentaire du théorème sur la distribution des nombres premiers. Scriptum 1, Centre Mathématique, Amsterdam, 1949.
• Selberg, A. An Elementary Proof of the Prime Number Theorem, Ann. Math. 50, 305—313, 1949.

§ 3. Законы больших чисел

Определение 52.
Говорят, что последовательность
с конечными удовлетворяет закону больших чисел
(ЗБЧ), если

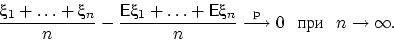(22)

Законами больших чисел принято называть утверждения о том, при каких условиях
последовательность случайных величин удовлетворяет закону больших чисел, т.е.
обладает свойством (22).

Выясним сначала, когда выполнен ЗБЧ для последовательности
и .

Теорема 33   (ЗБЧ Чебышёва).

Для любой последовательности и с конечным
имеет место сходимость:

(23)

Заметим, что если величины одинаково распределены, то их
одинаковы (и равны, например, ),
поэтому свойство можно записать в виде .

ЗБЧ утверждает, что среднее арифметическое большого числа
случайных слагаемых «стабилизируется» с ростом этого числа.
Как бы сильно каждая случайная величина не отклонялась от своего среднего значения,
при суммировании эти отклонения «взаимно гасятся»,
так что среднее арифметическое приближается к постоянной величине.

мы увидим, что требование конечности
(или дисперсии) связано исключительно со способом доказательства,
и что утверждение останется верным, если требовать существования
только .

Доказательство.

Обозначим через
сумму первых случайных величин.
Из математического ожидания получим:

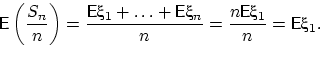
Пусть .
Воспользуемся :

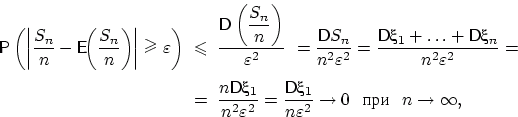(24)

так как .
Заметим, что дисперсия суммы превратилась в сумму дисперсий в силу слагаемых, из-за которой все ковариации в обратились в нуль при .
Сумма же дисперсий слагаемых равняется из-за их одинаковой
распределённости.

QED

Замечание 24.
Мы не только доказали сходимость, но и
получили оценку для вероятности среднему арифметическому
любого числа и величин
отличаться от более, чем на заданное :

(25)

Легко видеть, что попарную независимость слагаемых в ЗБЧ Чебышёва можно
заменить их , ничего не меняя в доказательстве.
ЗБЧ может выполняться и для последовательности зависимых и разнораспределённых слагаемых.
Предлагаю читателям, проследив за равенствами и неравенствами
, получить доказательство следующего утверждения,
предлагающего достаточные условия выполнения ЗБЧ для последовательности произвольных случайных величин.

Теорема 34   (ЗБЧ Маркова).

Последовательность случайных величин с конечными

при выполнении любого из следующих условий:

а)

если , т.е. если
при ;

б)

если независимы и
  (т.е. если
  )

в)

если независимы, одинаково распределены и имеют конечную дисперсию
().

Теорема Маркова утверждает, что , если
слагаемых растёт не слишком быстро с ростом .

Сильная зависимость слагаемых приводит обычно
к невыполнению ЗБЧ. Если, например, и , то , и свойство 
не выполнено (убедиться!).
В этом случае ; для одинаково распределённых
слагаемых дисперсия суммы быстрее расти не может.

Следующее утверждение мы докажем чуть позже. Сравните его условия с условиями
.

Теорема 35   (ЗБЧ Хинчина).

Для любой последовательности
и с конечным
имеет место сходимость:

Более того, в условиях теоремы имеет место
и последовательности
к . Это утверждение называется усиленным законом больших чисел (УЗБЧ) Колмогорова,
и его мы доказывать не будем.

Получим в качестве следствия из закон больших чисел
Я. Бернулли. В отличие от ЗБЧ Чебышёва, описывающего
предельное поведение среднего арифметического случайных величин с произвольными
распределениями, ЗБЧ Бернулли имеет дело лишь со .

Теорема 36   (ЗБЧ Бернулли).

Пусть событие может произойти в любом из с одной и той же вероятностью
, и пусть события
в испытаниях. Тогда .
При этом для любого

Доказательство. Заметим, что есть сумма ,
, имеющих
с параметром ( того, что в соответствующем испытании произошло ):
, где

и ,
.
Осталось воспользоваться и неравенством
.

QED

1Александр Яковлевич Хинчин (19.07.1894 18.11.1959)

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

N.Ch.

Взглянем на статистику

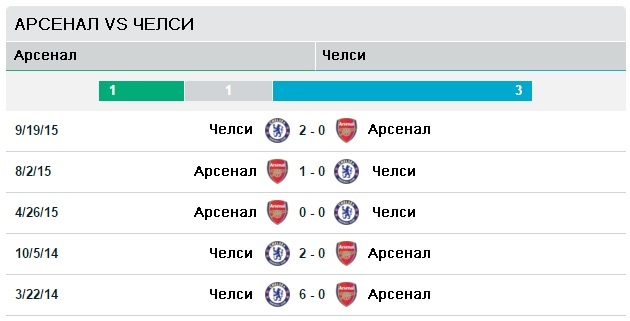
Почти две сотни матчей провели между собой непримиримые соперники по испанскому чемпионату мадридский «Реал» и «Барселона». Точнее – 198. Такое число может приблизить нас несколько к пониманию закона. Ничьи примем за результат, который не даёт преимущества ни одной стороне, поэтому не будем их учитывать. Так вот, королевский клуб одержал за всю историю противостояний 83 победы, их соперники из Каталонии – 77. Взлёты и падения были у каждого из этих клубов, но количество побед в общем показывает нам относительный паритет между соперниками.

Ещё больше матчей между собой провели «Ливерпуль» и «Арсенал» — 224 встречи, и здесь просматривается некоторое равенство. «Ливерпуль» одержал 86 побед, канониры – 78. История встреч миланских клубов тоже представляет собой относительное равенство побед и ничьих. У «Милана» 57 побед при 65 поражениях и 56 ничьих.

Смотреть что такое «БОЛЬШИХ ЧИСЕЛ ЗАКОН» в других словарях:

Больших чисел закон выражен в ряде… … Политология.

Неравенство Чебышева можно применять для любых случайных величин.

Не следует думать, что подобного рода затруднения являются какой-то особенностью теории вероятностей. Такая пропорциональность точности действия вероятностных закономерностей квадратному корню из числа наблюдений типична и для многих других вопросов. Иногда говорят даже в порядке несколько упрощенной популяризации о «законе квадратного корня из n» как основном законе теории вероятностей. Чебышев дал почти полное доказательство этой формулы для случая независимых и ограниченных слагаемых. Формула (28) охватила столь большое число частных задач, что долгое время ее называли центральной предельной теоремой теории вероятностей.

Алгебраическая теория чисел

Основная статья: Алгебраическая теория чисел

В алгебраической теории чисел понятие целого числа расширяется, в качестве алгебраических чисел рассматривают корни многочленов с рациональными коэффициентами. Была разработана общая теория алгебраических и трансцендентных чисел. При этом аналогом целых чисел выступают целые алгебраические числа, то есть корни унитарных многочленов с целыми коэффициентами. В отличие от целых чисел, в кольце целых алгебраических чисел не обязательно выполняется свойство факториальности, то есть единственности разложения на простые множители.

Теория алгебраических чисел обязана своим появлением изучению диофантовых уравнений, и в том числе попыткам доказать великую теорему Ферма. Куммеру принадлежит равенство

xn=zn−yn=∏i=1n(z−aiy),{\displaystyle x^{n}=z^{n}-y^{n}=\prod _{i=1}^{n}(z-a_{i}y),}

где ai{\displaystyle a_{i}} — корни степени n{\displaystyle n} из единицы.
Таким образом, Куммер определил новые целые числа вида z+aiy{\displaystyle z+a_{i}y}. Позднее Лиувилль показал, что если алгебраическое число является корнем уравнения степени n{\displaystyle n}, то к нему нельзя подойти ближе чем на Q−n{\displaystyle Q^{-n}}, приближаясь дробями вида PQ{\displaystyle P/Q}, где P{\displaystyle P} и Q{\displaystyle Q} — целые взаимно простые числа.

После определения алгебраических и трансцендентных чисел в алгебраической теории чисел выделилось направление, которое занимается доказательством трансцендентности конкретных чисел, и направление, которое занимается алгебраическими числами и изучает степень их приближения рациональными и алгебраическими.

Одним из основных приёмов является вложение поля алгебраических чисел в своё пополнение по какой-то из метрик — архимедовой (например, в поле вещественных или комплексных чисел) или неархимедовой (например, в поле p-адических чисел).