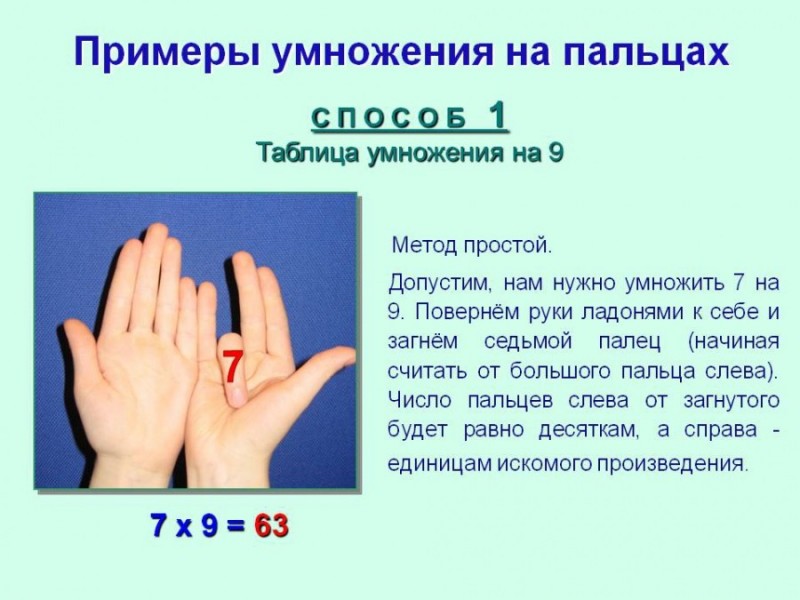
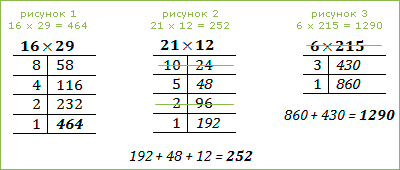Умножение чисел, формула
Содержание:
Выбираем традиционные методы
Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.
Умножение с помощью разложения чисел
Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки. Четыре полученных числа суммируются
Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме
Например, для умножения 38 на 57 необходимо:
- разложить число на (30+8)*(50+7);
- 30*50 = 1500 – запомнить результат;
- 30*7 + 50*8 = 210 + 400 = 610 – запомнить;
- (1500 + 610) + 8*7 = 2110 + 56 = 2166
Естественно, необходимо отлично знать таблицу умножения, так как быстро умножать в уме этим способом не удастся без соответствующих умений.
Умножение в столбик в уме
Визуальное представление привычного перемножения в столбик многие используют при расчетах. Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:
- 47*1 = 47 – запомнить;
- 47*8 = 376 – запоминаем;
- 376*10 + 47 = 3807.
Запоминать промежуточные результаты поможет проговаривание их вслух с одновременным суммированием в уме. Несмотря на сложность мысленных вычислений, после непродолжительных тренировок этот метод станет вашим любимым.
Приведенные выше способы умножения универсальны. Но знание более эффективных алгоритмов для некоторых чисел намного сократит количество расчетов.
Умножение на 11
Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.
Достаточно между цифрами множителя вставить их сумму:13*11 = 1(1+3)3 = 143
Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.28*11 = 2 (2+8) 8 = 308
Умножение больших чисел
Очень удобно перемножать числа, близкие к 100 разложением их на составляющие. Например, необходимо умножить 87 на 91.
- Каждое число необходимо представить как разницу 100 и еще одного числа:(100 — 13)*(100 — 9) Ответ будет состоять из четырех цифр, две первые из которых – разница первого множителя и вычитаемого из второй скобки или наоборот – разница второго множителя и вычитаемого из первой скобки.87 – 9 = 78 91 – 13 = 78
- Вторые две цифры ответа — результат перемножения вычитаемых из двух скобок.
13*9 = 144
- В результате получаются числа 78 и 144. Если при записывании окончательного результата получается число из 5 цифр вторую и третью цифру суммируем.
Результат: 87*91 = 7917.
Это самые простые способы перемножения. После многократного их применения, доведения вычислений до автоматизма можно осваивать более сложные техники. И через некоторое время проблема, как быстро умножить двузначные числа перестанет вас волновать, а память и логика существенно улучшатся.
Быстрый счет без калькулятора
Жизнь любого современного человека неотрывно связана с числами. Без умения считать невозможно выполнять самые простые повседневные задачи. Конечно, сегодня у людей появились умные помощники – калькуляторы, смартфоны, компьютеры, но даже они могут иногда подвести – сломаться или не вовремя разрядиться. Да и не всегда можно полагаться на гаджеты, ведь на экзаменах в школе или в ВУЗе они не помогут. Именно поэтому многие люди стремятся научиться хорошо считать без помощи подручных средств. Особенно это актуально для школьников, ведь если с детства освоить техники быстрого устного счета, то и учеба в школе, и различные задачи во взрослой жизни будут даваться легче.
Есть еще одна серьезная причина для того, чтобы начать тренироваться хорошо считать в уме. Устный счет развивает человеческий мозг и способствует росту уровня интеллекта. Поэтому даже те студенты, которые обучаются на гуманитарных специальностях, все равно изучают такие точные науки, как высшая математика и математический анализ. Упражнения, направленные на устный счет больших чисел, являются отличной зарядкой для ума. Так развитие интеллекта и удобство в быту – это две самые главные причины научиться хорошо считать без калькулятора.
Человечество еще с древности стремилось найти такие способы быстрого счета. И речь не только о простых вычислениях, таких как сложение и вычитание, но и о более сложных – об умножении и делении. Пусть это и занимает много времени, но складывать и вычитать большие значения все же можно без предварительной подготовки, а вот такие действия, как умножение двузначных чисел, недоступны большинству людей.
Но, благодаря труду математиков со всего земного шара, сегодня появились некоторые математические хитрости, позволяющие считать в уме не только однозначные, но и двузначные числа. Чтобы понять принцип их работы, лучше рассмотреть каждый из этих приемов отдельно.
Популярная система быстрого счета
Существует несколько видов основных математических операций – сложение, вычитание, умножение и деление. И если с нахождением суммы и разности все более или менее понятно, то другие вычисления производить намного сложнее. Рассмотрим самые популярные математические хитрости, направленные на удобное умножение и деление в уме.
Умножение любого числа на 9
Решать устно такие примеры очень легко. Для этого достаточно умножить нужное значение на 10 и вычесть из получившегося ответа это же число. Например, нам нужно найти результат умножения 19 и 9. Пример будет выглядеть так: 19*10-19= 190-19=171. Этот прием достаточно легко применять на практике.
Умножение любого числа на 11
Похожим образом выглядит умножение любого значения на 11: мы находим произведение нашего числа и 10, а затем прибавляем к получившемуся выражению наше число. Допустим, мы ищем сколько будет 67*11, так у нас получается следующий пример: 67*10+67=670+67=737.
Умножение двузначного числа на однозначное
Проще всего производить такую операцию методом разбора множителей на десятки и единицы. Допустим, нам требуется перемножить 56 и 8. Для этого мы разделяем 56 на составные части, получается 50 и 6. Теперь мы отдельно перемножаем наши десятки и единицы на однозначное число и ищем их сумму. Получается 50*8+6*8=400+48=448. Но чем больше знаков в каждом из перемножаемых значений, тем сложнее производить подобные операции в уме.
Умножение двузначного числа на двузначное
Нахождение результата умножения двузначных чисел похоже на предыдущий метод. К примеру, необходимо найти произведение 24 и 52. Для этого мы разбиваем одно из чисел на десятки и единицы и перемножаем их на наш множитель, а затем складываем полученные выражения: 20*52+4*52=1040+208=1248. Чем больше каждое из чисел, тем сложнее находить результат умножения.
Нахождение процента от числа
Чтобы найти процент от любого значения, нужно умножить данное число на размер искомого процента и разделить на сто. Лучше рассмотреть данный подход на примере. Допустим, требуется найти 12% от 74. Мы производим умножение 12 и 74, разбирая это выражение на составные части. Получается 10*74+2*74=740+148=888. Теперь мы делим наш результат на 100 и получаем ответ – 8,88%. Так удается легко находить процент от любого значения без помощи калькулятора.
Деление многозначного числа на однозначное
Чтобы найти ответ на такой пример, нужно вспомнить таблицу умножения. Допустим, нам требуется разделить число 138 на 6. Для этого мы разбиваем делимое на части, получается 13 десятков и 8 единиц. Делим 13 на 6, получаем 2 и 1 в остатке. Это значит, что десятком в нашем ответе будет число 2. Остаток, а это 1 десяток, мы складываем с единицей делимого, получается 18. Делим 18 на 6, получается 3. Теперь складываем получившиеся десятки и единицы: 20+3=23. Целое выражение будет выглядеть так: 120/6+(10+8)/6=20+18/6=23.
Существуют и другие, более сложные приемы устных математических вычислений, которые позволяют выполнять операции с многозначными числами. Но и освоить эти техники труднее, так как они требуют высокой концентрации и хорошо развитой памяти.
К плюсам всех подобных приемов можно отнести уже то, что такому счету можно научиться достаточно быстро. Перечисленные способы имеют множество вариаций от простых до более сложных, поэтому некоторые из них охотно используют даже дети. Но все эти методы имеют один существенный недостаток, который не позволяет им называться полноценной системой счета в уме.
Такие способы вычислений подразумевают соблюдение целого ряда условий. Например, правила для умножения трехзначных чисел отличаются от правил для двузначных. Поэтому приходится запоминать большое количество условий, чтобы можно было применять в быту такие способы счета. Все это делает подобные методы сложения, вычитания, умножения и деления скорее зарядкой для ума, чем продуктивным подходом к вычислениям.
Но существуют и кардинально иные техники, позволяющие развить навыки человека и научиться очень хорошо считать без подручных средств. Одной из самых популярных методик быстрого устного счета является ментальная арифметика. Рассмотрим ее преимущества подробнее.

Секреты устного счёта
Существуют приемы устного счета — простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.
Прибавляем числа 7,8,9
Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.
Примеры:
56+7=56+10-3=63
47+8=47+10-2=55
73+9=73+10-1=82
Быстро складываем двузначные числа
Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».
Примеры:
54+39=54+40-1=93
26+38=26+40-2=64
Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем — единицы.
Пример:
57+32=57+30+2=89
Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:
32+57=32+60-3=89
Складываем в уме трехзначные числа
Быстрый счет и сложение трехзначных чисел — это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.
Пример:
249+533=(200+500)+(40+30)+(9+3)=782
Особенности вычитания: приведение к круглым числам
Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.
Примеры:
67-9=67-10+1=58
576-88=576-100+12=488
Вычитаем в уме трехзначные числа
Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.
Пример:
843-596=843-500-90-6=343-90-6=253-6=247
Умножить и разделить
Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения — это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!
Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:
15*16=15*10+(10*6+5*6)=150+60+30=240
Умножаем и делим на 4, 6, 8, 9
Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.
Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:
-
умножить на 4 — это дважды умножить на 2;
-
умножить на 6 — это значит умножить на 2, а потом на 3;
-
умножить на 8 — это трижды умножить на 2;
-
умножить на 9 — это дважды умножить на 3.
Например:
37*4=(37*2)*2=74*2=148;
412*6=(412*2)·3=824·3=2472
Аналогично:
-
разделить на 4 — это дважды разделить на 2;
-
разделить на 6 — это сначала разделить на 2, а потом на 3;
-
разделить на 8 — это трижды разделить на 2;
-
разделить на 9 — это дважды разделить на 3.
Например:
412:4=(412:2):2=206:2=103
312:6=(312:2):3=156:3=52
Как умножать и делить на 5
Число 5 — это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.
Пример:
326*5=(326*10):2=3260:2=1630
Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.
326:5=(326·2):10=652:10=65,2.
Умножение на 9
Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:
37*9=(37*3)*3=111*3=333
или
37*9=37*10 — 37=370-37=333
Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.
Выполнение умножения
При практическом решении задачи умножения двух чисел необходимо свести её к последовательности более простых операций: «простое умножение», сложение, сравнение и др. Для этого разработаны различные методы умножения, например для чисел, дробей, векторов и др. На множестве натуральных чисел в настоящее время используется алгоритм поразрядного умножения. При этом следует рассматривать умножение как процедуру (в отличие от операции).
Примерный алгоритм процедуры поразрядного умножения двух чисел
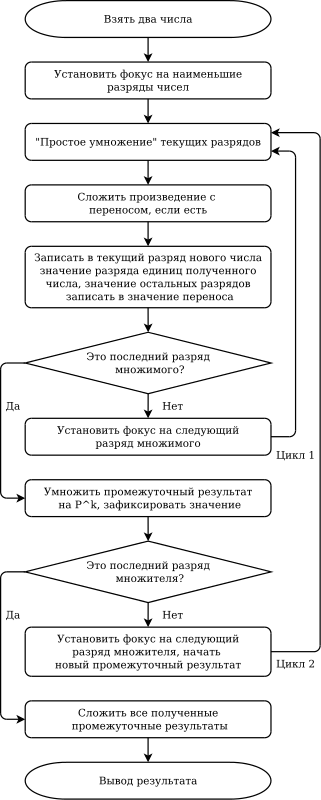
Процедура достаточно сложная, состоит из относительно большого числа шагов и при умножении больших чисел может занять продолжительное время.
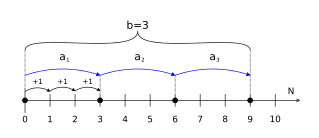
Пример пошагового умножения 3 ∙ 3 = 9 на числовой прямой.
«Простое умножение» в данном контексте обозначает операцию умножения одноразрядных чисел, которая может быть легко сведена к сложению. Является гипероператором сложения:
a⋅b=hyper2(a,b)=hyper(a,2,b)=a(2)b.{\displaystyle a\cdot b=\operatorname {hyper2} (a,b)=\operatorname {hyper} (a,2,b)=a^{(2)}b.}
a(2)b=a⋅b=a+a+⋯+a⏟b.{\displaystyle a{^{(2)}}b=a\cdot b=\underbrace {a+a+\dots +a} _{b}.}
где a+a+⋯+a{\displaystyle a+a+\dots +a} — последовательное сложение b{\displaystyle b} элементов.
Чтобы упростить и ускорить процесс умножения используют табличный метод «простого умножения», для этого заранее вычисляют все комбинации произведений чисел от 0 до 9 и берут готовый результат из этой таблицы:
Таблица для умножения в десятичной системе счисления
| * | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
Данная процедура применима к умножению натуральных и целых (с учётом знака) чисел. Для других чисел используются более сложные алгоритмы.
Полезные рекомендации

Чтобы постоянно тренироваться в устном счете и не придумывать себе примеры, достаточно скачать мобильное приложение. Существует много методичек по ведению устного счета. В них описаны разные техники. Стоит опробовать несколько вариантов, чтобы выбрать подходящую методику, которую удобно использовать в повседневной жизни.
Также в процессе вычислений можно применять следующие полезные советы:
-
- Чтобы быстро отнять от любого числа 9, достаточно вычесть из него 10 и прибавить один. Аналогично поступают при отнимании восьми, только прибавляют в этом случае 2. При вычитании семерки отнимают 10, а прибавляют три.
- Если нужно быстро умножить на 9, то к исходному значению приписывают в конце ноль (то есть множат на 10), а потом вычитают из результата само число. Например, 75х9=750-75=675.
- Чтобы легко и быстро умножить сложную цифровую комбинацию на 2, ее округляют до более простого значения, например, 239 округляют до 240 и множат на 2, получив 480, вычитают 2, потому что единица, на которую округлили при умножении на два, дает 2. Операция выглядит так: 240х2-1х2=480-2=478.
- При делении на два сложного цифрового значения также прибегают к округлению. Допустим, нужно разделить 198 на 2. Число округляют до 200 и делят на два, а потом отнимают 1, потому что прибавленные две единицы при делении на 2 дают 1. Получается: 198:2=200:2-2:2=100-1=99.
- При умножении и делении на 8 и 4 не забывают, что, по сути, эти операции являются многократным делением или умножением на два. В связи с этим лучше последовательно выполнять операцию. Например, 89х4=89х2х2=178х2=356.
- Умножение на пять напоминает деление на два. Для быстрого умножения сложной комбинации на 5, достаточно поделить ее на два и прибавить в конце ноль. Например, 88х5=88:2=44 плюс 0, то есть получится 440.
Чтобы при подсчете в уме не ошибиться, заранее определяют диапазон цифрового значения результата. Так, при умножении однозначных чисел результат никогда не будет больше 90, потому что 9 на 9 равно 81. При умножении двузначных цифр результат не может превышать 10 тысяч. Если речь идет о трехзначных множителях, то полученное значение не может превышать 1 000 000.
Деление чисел со степенями
Если степени разные, но основания одинаковые, то действия производим согласно правилу, описанному выше. А именно:
Если же разные и степени, и основания, то возводим в степень каждое число и только потом умножаем:
33 ÷52 = 27÷25 = 1,08
Подготовиться к сложной контрольной ребенку помогут в детской онлайн-школе Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Запишите вашего ребенка на бесплатный вводный урок математики и начните заниматься ей с удовольствием уже завтра.