Эллипс. формулы, признаки и свойства эллипсa
Содержание:
Делаем овальные конструкции из ГКЛ самостоятельно

Сегодня из гипсокартона можно сделать любой фигурный потолок разного уровня сложности. Кто-то предпочитает сложные прямоугольные или квадратные конструкции, а кому-то нравятся овалы или эллипсы с грациозными изогнутыми линиями
Овальные потолки особо притягивают внимание. Гармонично вписываясь в дизайн интерьера, смотрятся они изысканно и оригинально
Однако сделать их порядком сложнее, чем квадратные или прямоугольные. Без чертежа тут явно не обойтись. Предлагаем Вашему вниманию пошаговую инструкцию и советы экспертов.
Овал в переводе с французского означает яйцо. То есть это фигура яйцеобразной формы, которая ограничена кривой линией. Многие отождествляют понятия овала и эллипса. Однако хоть эллипс внешне и похож на овал, таковым он не является. Эллипс принадлежит к лекальным кривым.
Соотношения между элементами эллипса
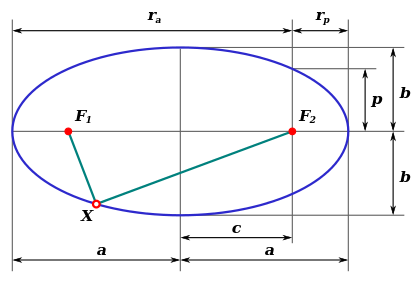
Части эллипса (описание см. в разделе «Связанные определения»)
- a{\displaystyle {\boldsymbol {a}}} — большая полуось;
- b{\displaystyle {\boldsymbol {b}}} — малая полуось;
- c{\displaystyle {\boldsymbol {c}}} — фокальное расстояние (полурасстояние между фокусами);
- p{\displaystyle {\boldsymbol {p}}} — фокальный параметр;
- rp{\displaystyle {\boldsymbol {r}}_{p}} — перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
- ra{\displaystyle {\boldsymbol {r}}_{a}} — апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);
a2=b2+c2{\displaystyle a^{2}=b^{2}+c^{2}}
e=ca=1−b2a2(⩽e<1).{\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leqslant e<1).}.
p=b2a{\displaystyle p={\frac {b^{2}}{a}}}
| a{\displaystyle {\boldsymbol {a}}} | b{\displaystyle {\boldsymbol {b}}} | c{\displaystyle {\boldsymbol {c}}} | p{\displaystyle {\boldsymbol {p}}} | rp{\displaystyle {\boldsymbol {r_{p}}}} | ra{\displaystyle {\boldsymbol {r_{a}}}} | |
|---|---|---|---|---|---|---|
| a{\displaystyle {\boldsymbol {a}}} — большая полуось | a{\displaystyle {\boldsymbol {a}}} | a=b1−e2{\displaystyle a={\frac {b}{\sqrt {1-e^{2}}}}} | a=ce{\displaystyle a={\frac {c}{e}}} | a=p1−e2{\displaystyle a={\frac {p}{1-e^{2}}}} | a=rp1−e{\displaystyle a={\frac {r_{p}}{1-e}}} | a=ra1+e{\displaystyle a={\frac {r_{a}}{1+e}}} |
| b{\displaystyle {\boldsymbol {b}}} — малая полуось | b=a1−e2{\displaystyle b=a{\sqrt {1-e^{2}}}} | b{\displaystyle {\boldsymbol {b}}} | b=c 1−e2e{\displaystyle b={\frac {c~{\sqrt {1-e^{2}}}}{e}}} | b=p1−e2{\displaystyle b={\frac {p}{\sqrt {1-e^{2}}}}} | b=rp1+e1−e{\displaystyle b=r_{p}{\sqrt {\frac {1+e}{1-e}}}} | b=ra1−e1+e{\displaystyle b=r_{a}{\sqrt {\frac {1-e}{1+e}}}} |
| c{\displaystyle {\boldsymbol {c}}} — фокальное расстояние | c=ae{\displaystyle c=ae} | c=be1−e2{\displaystyle c={\frac {be}{\sqrt {1-e^{2}}}}} | c{\displaystyle {\boldsymbol {c}}} | c=pe1−e2{\displaystyle c={\frac {pe}{1-e^{2}}}} | c=rpe1−e{\displaystyle c={\frac {r_{p}e}{1-e}}} | c=rae1+e{\displaystyle c={\frac {r_{a}e}{1+e}}} |
| p{\displaystyle {\boldsymbol {p}}} — фокальный параметр | p=a(1−e2){\displaystyle p=a(1-e^{2})} | p=b 1−e2{\displaystyle p=b~{\sqrt {1-e^{2}}}} | p=c 1−e2e{\displaystyle p=c~{\frac {1-e^{2}}{e}}} | p{\displaystyle {\boldsymbol {p}}} | p=rp(1+e){\displaystyle p=r_{p}(1+e)} | p=ra(1−e){\displaystyle p=r_{a}(1-e)} |
| rp{\displaystyle {\boldsymbol {r}}_{p}} — перифокусное расстояние | rp=a(1−e){\displaystyle r_{p}=a(1-e)} | rp=b 1−e1+e{\displaystyle r_{p}=b~{\sqrt {\frac {1-e}{1+e}}}} | rp=c 1−ee{\displaystyle r_{p}=c~{\frac {1-e}{e}}} | rp=p1+e{\displaystyle r_{p}={\frac {p}{1+e}}} | rp{\displaystyle {\boldsymbol {r}}_{p}} | rp=ra1−e1+e{\displaystyle r_{p}=r_{a}{\frac {1-e}{1+e}}} |
| ra{\displaystyle {\boldsymbol {r}}_{a}} — апофокусное расстояние | ra=a(1+e){\displaystyle r_{a}=a(1+e)} | ra=b 1+e1−e{\displaystyle r_{a}=b~{\sqrt {\frac {1+e}{1-e}}}} | ra=c 1+ee{\displaystyle r_{a}=c~{\frac {1+e}{e}}} | ra=p1−e{\displaystyle r_{a}={\frac {p}{1-e}}} | ra=rp 1+e1−e{\displaystyle r_{a}=r_{p}~{\frac {1+e}{1-e}}} | ra{\displaystyle {\boldsymbol {r}}_{a}} |
Построение дуги окружности. Произвольная дуга, дуга по трем точкам, дуга касательная к кривой.
Программа “Компас 3D” располагает несколькими методами, позволяющими построить дугу окружности различных типов. Включая произвольную дугу, дугу по трём точкам, дугу касательно к кривой, дугу по двум точкам, дугу по двум точкам и углу раствора. Данная статья ознакомит вас с некоторыми методами. Которые позволят получить дугу окружности.
Произвольная дуга окружности.
Для того, чтобы построить произвольную дугу, вам нужно нажать кнопку “Дуга” в панели компакта или найти её в меню сверху. Где оно скрыто за командами “Инструменты” – “Геометрия” – “Дуги” – “Дуга”.
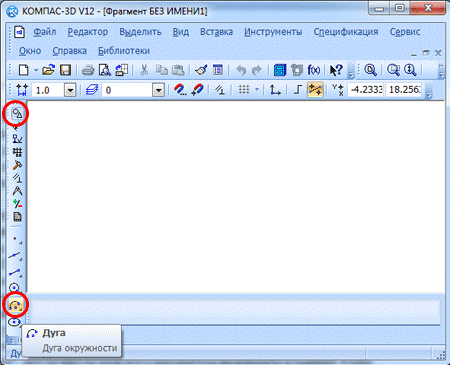
С помощью указателя мышки вы сначала можете задать начало дуги и её центральную точку. Также вы сможете ввести положение точки начала дуги в свойственной панели. После того, как зададите размеры угла и радиуса или диаметра в нужных пунктах меню. По умолчанию задаются параметры радиуса. Итак, перейдём к постановке дуги, имеющей центр в начале координатной оси. Начальная точка указывается с учётом радиуса в 30 мм и угла в 150 градусов. После ввода данных, вам нужно будет нажать клавишу ввода или переноса.
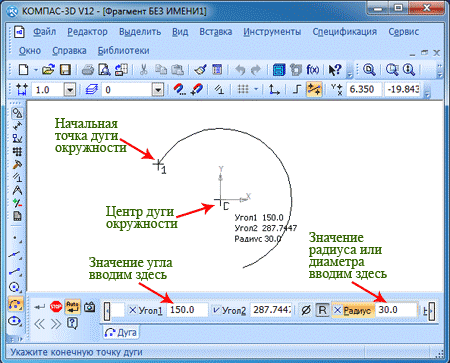
После этого с помощью курсора или введя значение угла, вы указываете координаты точки, где будет заканчиваться дуга. Например, можем задать угол в 10 градусов.
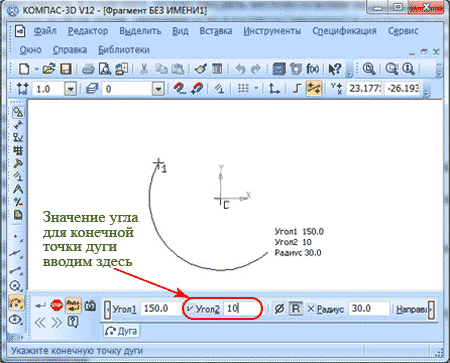
После нажатия клавиши ввода, дуга будет строиться автоматически.
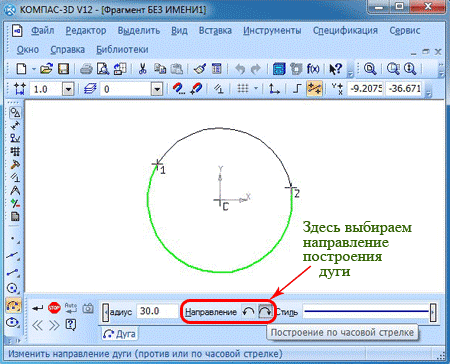
По умолчанию построение дуги заданно как построение против часовой стрелки.
Если вы желаете задать обратное направление. В панели свойств есть отдельный пункт меню, где вы сможете ввести изменения в установки по умолчанию, как на картинке выше.
Дуга по трем точкам.
Для того, чтобы построить дугу с трема точками, вам нужно нажать кнопку “Дуга по 3 точкам”. Которая находится в панели компактного меню или же сверху в меню. Где нужно последовательно нажать на пункты “Инструменты” – “Геометрия” – “Дуги” – “Дуга по 3 точкам”.
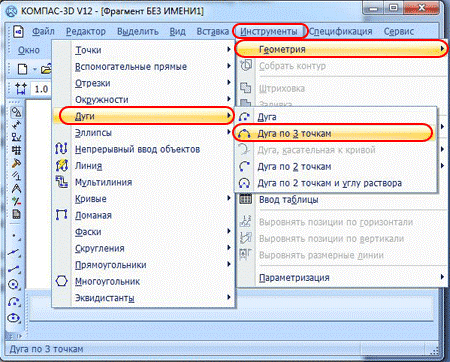
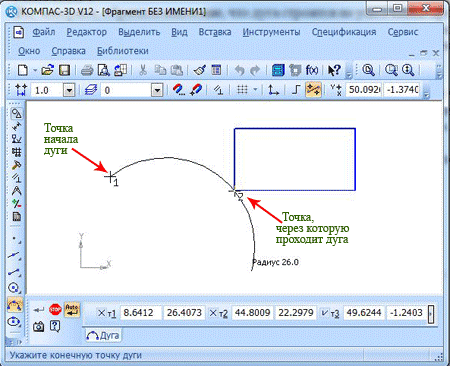
С помощью курсора мыши, вы получите возможность последовательного указания токи, где дуга будет начинаться, точки, через которую дуга должна проходить (такой точкой может быть, например, вершина прямоугольника), а также точки, в которой дуга будет заканчиваться. В данном случае система сможет самостоятельно просчитать координаты центральной точки и радиус дуги.
Дуга касательная к кривой.
Для того, чтобы построить касательную к кривой линии дугу, вам нужно нажать кнопку “Дуга касательная к кривой”. В компактной панели, или же в меню сверху, где вам предстоит нажать команды “Инструменты” – “Геометрия” – “Дуги” – “Дуга касательная к кривой”.
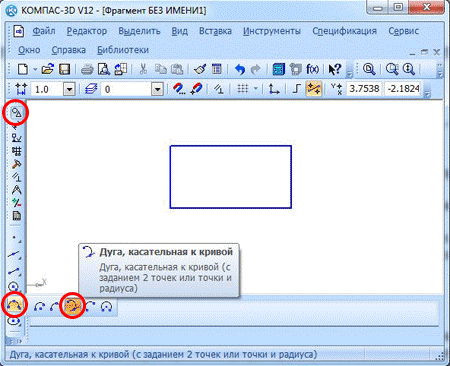
Вам нужно задать точку, через которую пройдёт будущая дуга, а также точку, где дуга будет заканчиваться, с помощью курсора мыши. Система способна рассчитать по умолчанию, какими будут радиус и координаты центральной точки дуги. Начало дуги будет лежать в точке соприкосновения.
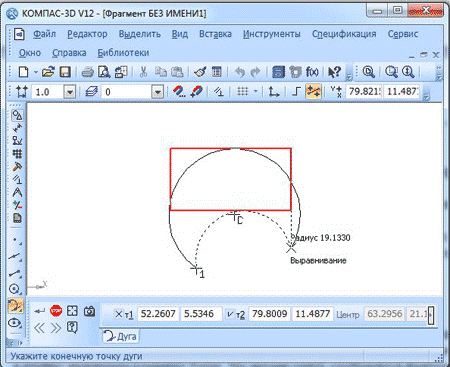
После того, как вы укажете точки, экран покажет вам фантомные варианты различных возможностей и вариантов построения дуги. Вам нужно будет выбрать тот, который подходит именно вам. Далее вы должны будете зафиксировать данный вариант с помощью курсора. В завершение построения нужно нажать кнопки “Создать объект” и “Прервать команду”.
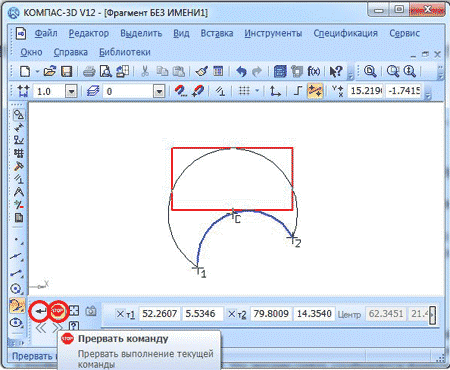
Если вы знаете радиус, предписанный касательной дуге, у вас есть возможность ввода его в нужное поле панели свойств.
К примеру, можем заняться построением дуги касательной к прямоугольнику с радиусом в 50 мм.
После того, как вы закончили ввод значений в ячейки, вам нужно нажать клавишу ввода. Экран опять покажет фантомные варианты построения дуг.
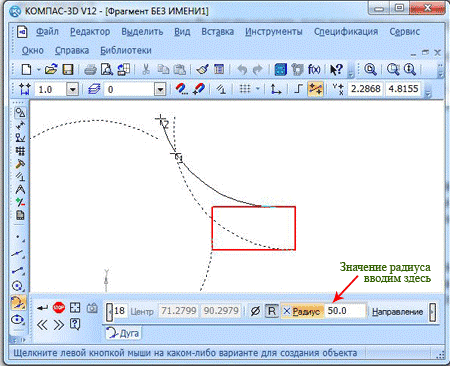
Как и раньше, нужно выбрать соответствующий вам вариант и зафиксировать его.
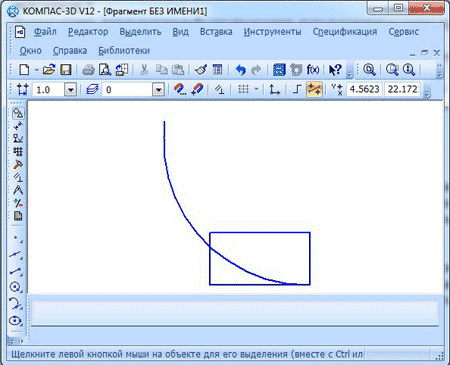
Стоит помнить о том, что не всегда является возможным построение дуги касательной с помощью указания радиуса. О том, что это невозможно, вам сообщит исчезновение всех фантомных вариантов после того, как вы введете желаемый радиус.
Пока что, это всё. Существуют и другие способы построения дуг, которые мы покроем в следующих уроках.
Построение дуги окружности. Дуга по двум точкам, дуга по двум точкам и углу раствора.
Дуга по двум точкам.
Для того, чтобы построить дугу с указанием двух точек, вам нужно выбрать «Дуга по 2 точкам». В компактном меню либо же указать в меню сверху следующие команды «Инструменты» — «Геометрия» — «Дуги» — «Дуга по 2 точкам».
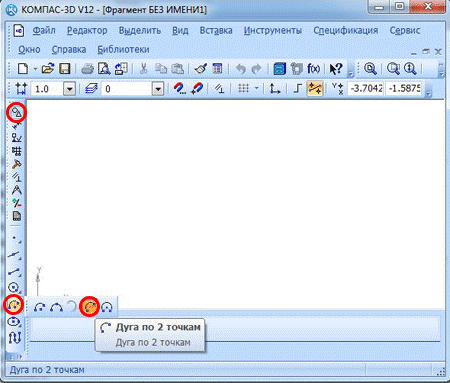
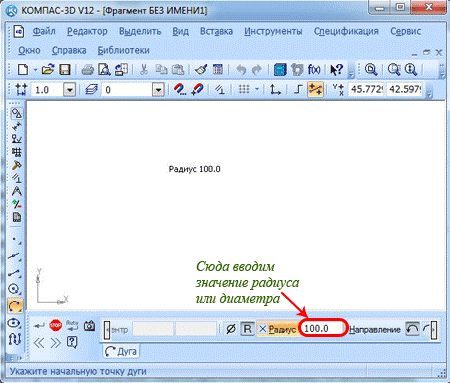
Для начала в нужном поле в свойственной панели от вас требуется ввести значение радиуса либо диаметра (к примеру, радиус в 100 мм) и нажать кнопку ввода.
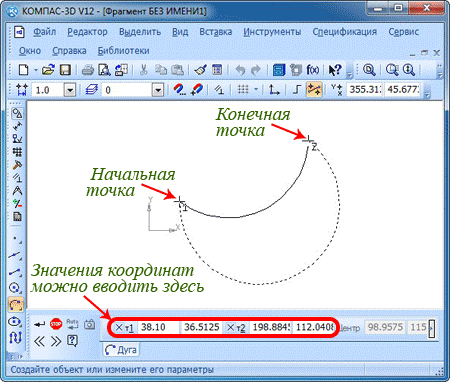
С помощью курсора или же в свойственной панели указываете координаты начала и конца дуги. Экран отобразит фантомные варианты построения.
Вам нужно выбрать правильный и последовательно нажать пункты «Создать объект» и «Прервать команду».
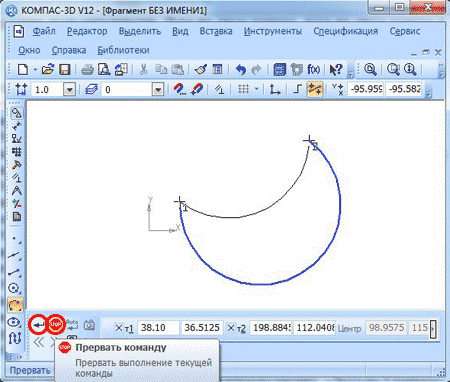
Если вы хотите построить дугу по диаметрально противоположным точкам, то радиус и диаметр программа рассчитает самостоятельно.
Дуга по двум точкам и углу раствора.
Для того, чтобы построить дугу с указанием двух точек и угла раствора, нужно нажать «Дуга по 2 точкам и углу раствора». В компактном меню или же в меню сверху выбрать команды «Инструменты» — «Геометрия» — «Дуги» — «Дуга по 2 точкам и углу раствора».
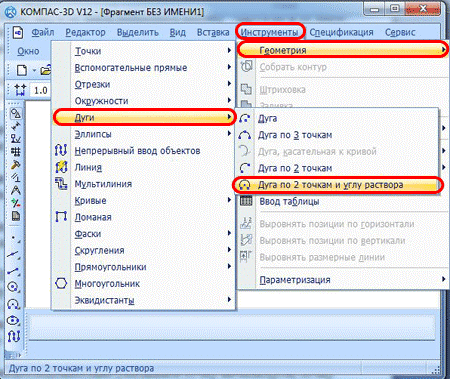
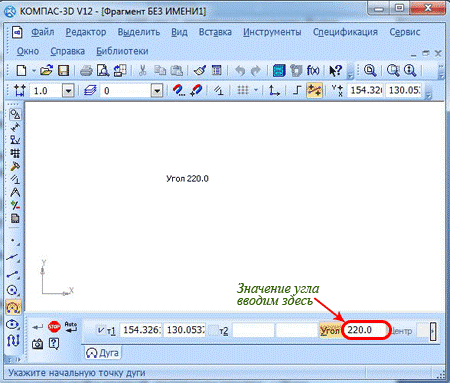
В свойственной панели для начала нужно ввести значение угла (к примеру, 220 градусов) и нажать клавишу ввода.
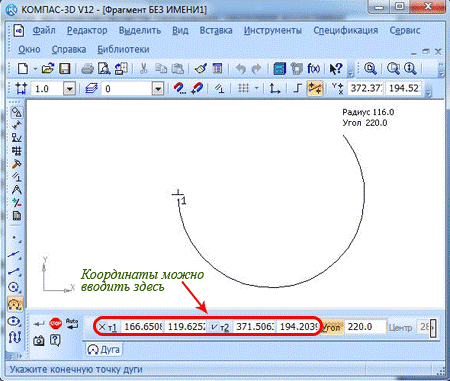
Потом вам нужно указать положение начала и конца дуги. Координаты могут указываться с помощью курсора либо введя их в нужные поля свойственной панели.
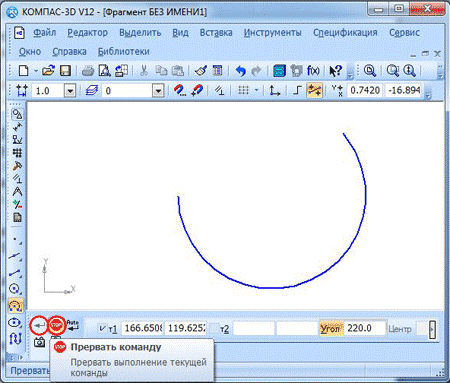
Прочие параметры, такие, как центральная точка и диаметр, программа определит самостоятельно. Построение завершается кнопками «Создать объект» и «Прервать команду».
Нами были рассмотрены все возможности построения дуг в “Компас 3D”. Далее мы разберёмся, как строить эллипсы.
Связанные определения
- Проходящий через фокусы эллипса отрезок AB, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
- Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
- Точка пересечения большой и малой осей эллипса называется его центром.
- Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
- Расстояния r1{\displaystyle r_{1}} и r2{\displaystyle r_{2}} от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
- Расстояние c=|F1F2|2{\displaystyle c={\frac {|F_{1}F_{2}|}{2}}} называется фокальным расстоянием.
- Величина e=ca=1−b2a2{\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}} называется эксцентриситетом.
- Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
- Радиус эллипса в данной точке это отрезок, соединяющий центр эллипса с точкой, а также его длина, которая вычисляется по формуле r=abb2cos2φ+a2sin2φ=b1−e2cos2φ{\displaystyle r={\frac {ab}{\sqrt {b^{2}\cos ^{2}\varphi +a^{2}\sin ^{2}\varphi }}}={\frac {b}{\sqrt {1-e^{2}\cos ^{2}\varphi }}}}, где φ{\displaystyle \varphi } — угол между радиусом и большой полуосью.
- Фокальным параметром p=b2a{\displaystyle p={\frac {b^{2}}{a}}} называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса.
- Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью: k=ba.{\displaystyle k={\frac {b}{a}}.} Величина, равная (1−k)=a−ba,{\displaystyle (1-k)={\frac {a-b}{a}},} называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент сжатия и эксцентриситет эллипса связаны соотношением k2=1−e2.{\displaystyle k^{2}=1-e^{2}.}
- Для каждого из фокусов существует прямая, называемая директрисой, такая, что отношение расстояния от произвольной точки эллипса до его фокуса к расстоянию от этой точки до данной прямой равно эксцентриситету эллипса. Весь эллипс лежит по ту же сторону от такой прямой, что и фокус. Уравнения директрис эллипса в каноническом виде записываются как x=±pe(1+e){\displaystyle x=\pm {\frac {p}{e\left(1+e\right)}}} для фокусов (∓p1+e,){\displaystyle \left(\mp {\frac {p}{1+e}},\,0\right)} соответственно. Расстояние между фокусом и директрисой равно pe.{\displaystyle {\frac {p}{e}}.}














