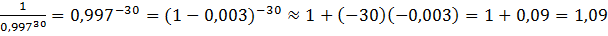Квадрат

Содержание:

История
Последние новости
Создание
Пример задачи с решением
- Задача №7
Величины, части и характеристики
Кубирование куба
- Гиперкубирование гиперкуба
Уравнение квадрата
Расчет угла Ганна для среднесрочной торговли

История

Вопрос о возможности разбиения квадрата на неравные квадраты был записан в Шотландской книге Станиславом Рузевичем под номером 59 в 1935-м году.
Самые первые найденные Бруксом, Смитом, Стоуном и Таттом совершенные квадраты были 69-го порядка.
В 1939 году Р. Шпраг (R. Sprague) нашёл совершенный квадрат 55-го порядка, это было первое опубликованное решение для совершенного квадрата.
Позднее Т. Г. Уиллкокс (T. H. Willcocks) нашёл совершенный квадрат 24-го порядка, который долгое время держал рекорд малости порядка.
В 1978 году голландский математик А. Й. В. Дёйвестейн (A. J. W. Duijvestijn) с помощью компьютера нашёл разбиение квадрата на 21 квадрат, среди которых нет равных (см. рис.). Он также доказал следующие утверждения:
- Не существует совершенного квадрата меньшего порядка.
- Найденное им разбиение — единственно возможное для разбиения 21-го порядка.

Создание

Квадрат декарта для принятия решений в 2018 году

Из-за бюджетных ограничений, Анатолий Иванов работал над фильмом как сценарист, сопродюсер, режиссёр, оператор, монтажёр и звукорежиссёр.

Подготовительный период

Анатолий Иванов сформулировал идею Квадрата после экспромтной съёмки и монтажа короткометражного 30-минутного фильма на Кантонском языке о частном гонконгском фестивале боевых искусств в феврале 2011. После чего, он предложил Андрею Пушкарёву снять реалистичный документальный фильм о работе диджея, когда оба встретились в парижской квартире режиссёра.

Анатолий Иванов объединил усилия с Юрием Рысевым чтобы профинансировать проект из частных источников, изначально ошибившись в размерах бюджета в 5 раз.

Его радикальный подход к кинопроизводству позволил снять полнометражный фильм в 5 странах, несмотря на маленький бюджет, в частности за счёт того, что все участвующие в нём работали добровольно и без какой-либо финансовой компенсации.

Места съёмок

Квадрат снимался исключительно на местности в:

Швейцарии
- Цюрихе
- Женеве
- Ольтене
Франции
- Париже
- Марселе
Венгрии
- Будапеште
- Кецеле
Румынии
- Бухаресте
- Крайове
- Клуж-Напоке
России
- Москве
- Санкт-Петербурге
- Ижевске
- Воткинске
- Степаново, Удмуртия

А также во время регулярных рейсов авиакомпаний SWISS и Ижавиа, железнодорожных переездов SBB CFF FFS, РЖД и поездок на женевских TPG, петербургском и московском метро.

Съёмочный период

Съёмки начались 27 августа 2011, закончились 16 июля 2012 и продолжались 55 дней (если считать те дни, когда работала камера).

Фильм был снят в формате 1080p HD парой камер Canon 1D mark IV и всего лишь двумя фото-объективами Canon.

Съёмочная группа состояла из одного человека. Анатолий Иванов снимал видео и записывал звук, неся всё кинооборудование на себе. Он не использовал тележки, краны, стедикамы, штативы и крепления для машин и полностью снял Квадрат с рук. Съёмки производились без какого-либо дополнительного освещения.

Монтаж и пост-продакшн

Монтаж в Final Cut Pro X и пост-продакш начались сразу после завершения съёмок. Процесс занял 1 год в Женеве и осложнялся техническими проблемами, такими как ретушь горячих пикселей на отснятом материале и неадекватными компьютерными средствами (один и пара наушников Sony MDR7506).

Музыка

Фильм содержит 35 треков (композиций) сыгранных диджеем Пушкарёвым, представляя различные жанры техно музыки, от дип-хауса до даб-техно, от минимал-техно до электро:

«Abyss» by Manoo — Deeply Rooted House, 2008
«Direct» by Kris Wadsworth — NRK Sound Division, 2009
«La Grippe (Helly Larson Remix)» by George Soliis — Wasabi, 2011
«Air» by Havantepe — Styrax Leaves, 2007
«Mauna Loa» by Mick Rubin — Musik Gewinnt Freunde, 2009
«Soul Sounds (Freestyle Man Original Dope Remix)» by Sasse — Moodmusic, 2005
«Tammer (David Duriez Remix From Da Vault)» by Phonogenic — 20:20 Vision, 2000
«Track B1» by Slowhouse Two — Slowhouse Recordings, 2008
«Post» by Claro Intelecto — Modern Love, 2011
«Acid Face» by Scott Findley — Iron Box Music, 2003
«Warriors» by Two Armadillos — Secretsundaze Music, 2007
«Grand Theft Vinyl (JV Mix)» by Green Thumb vs JV — So Sound Recordings, 2004
«Tobacco (Alveol Mix)» by Kiano Below Bangkok — Only Good Shit Records, 2011
«When The Dark Calls» by Pop Out and Play — Alola, 2001
«Circular Motion (Vivid)» by Christian Linder — Phono Elements, 2002
«Blacktro (Demo 1)» by Jerome Sydenham and Joe Claussell — UK Promotions, 2007
«Green Man» by Mr. Bizz — Deepindub.org, 2008
«Tahiti» by Ben Rourke — Stuga Musik, 2011
«Willpower» by Joshua Collins — Prolekult, 2002
«Lullaby For Rastko (Herb LF Remix)» by Petkovski — Farside, 2011
«Agape Dub» by Luke Hess — Modelisme Records, 2009
«Glacial Valley» by Makam — Pariter, 2011
«The Time» by Vizar — Jato Unit Analog, 2011
«Libido» by Sean Palm and Charlie Mo — Railyard Recordings, 2008
«Ahck (Jichael Mackson Remix)» by Minilogue — Wir, 2007
«Altered State (Artificial Remix)» by Jason Vasilas — Tangent Beats, 2004
«Modern Times (Dub Mix)» by Hatikvah — Baalsaal, 2009
«That Day (Loudeast Black Label Remix)» by DJ Grobas — Thrasher Home Recordings, 2004
«The Hills (John Selway Dub)» by Filippo Mancinelli and Allen May — Darkroom Dubs, 2011
«Running Man» by Petar Dundov — Music Man Records, 2007
«Ice» by Monolake — Imbalance Computer Music, 2000
«Lucky Punch» by Peter Dildo — Trackdown Records, 2006
«Live Jam 1» by Rhauder — Polymorph, 2011
«Can U Hear Shapes?» by Pop Out and Play — Alola, 2001
«Be No-One» by Charles Webster — Statra Recordings, 2001

Пример задачи с решением

Задача №7

Инженерный калькулятор онлайн с самыми точными расчетами!

Сократить дробь:

Решение.

В числителе записан квадрат разности, а в знаменателе – разность квадратов двух выражений. Применяя соответствующие формулы, получается искомый результат:

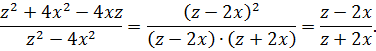
Ответ:

В большинстве случаев разницы, как сворачивать квадрат двучлена, не существует. Однако в данной ситуации, благодаря выражению в знаменателе, на первое место лучше поставить

Онлайн калькуляторы помогают выполнять преобразования. Однако, поскольку формулы сокращённого умножения являются базовым материалом школьного курса, то лучше не просто получить результат, но и понять, каким образом к нему пришли.

Предыдущая
МатематикаДесятичный логарифм в математике — свойства, условия и примеры вычислений
Следующая
МатематикаПризнаки делимости чисел — правила и примеры решений

Величины, части и характеристики

У квадрата, как и у любого многоугольника, есть вершины — это точки, в которых пересекаются его стороны. Вершины квадрата лежат на описанной вокруг него окружности. Через вершину в центр квадрата проходит диагональ, которая также является биссектрисой и радиусом описанной окружности.

Так как квадрат — это плоская фигура, то рассечь и построить сечение квадрата невозможно. Зато он может быть результатом пересечения многих объемных тел плоскостью. Например, цилиндра. Осевое сечение у цилиндра — прямоугольник или квадрат. Даже при пересечении тела плоскостью под произвольным углом может получиться квадрат!

Но у квадрата есть еще одно отношение к сечению, да не к какому-нибудь, а к Золотому сечению.

Все мы знаем, что Золотое сечение — это пропорция, в которой одна величина относится к другой так же, как их сумма к большей величине. В обобщенном процентном выражении это выглядит следующим образом: исходная величина (сумма) делится на 62 и 38 процентов.

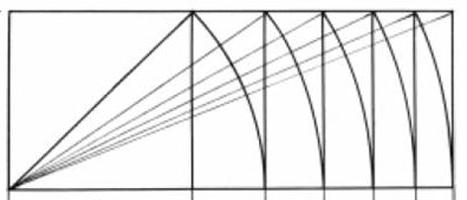
Да, для начала вам нужно построить квадрат. Его сторона будет равна меньшей стороне будущего прямоугольника. Затем необходимо провести диагональ этого квадрата и, воспользовавшись циркулем, длину этой диагонали отложить на продолжении стороны квадрата. Из полученной на пересечении точки выстраиваем прямоугольник, у которого снова строим диагональ и откладываем ее длину на продолжении стороны. Если продолжить работу по этой схеме, получатся те самые динамические прямоугольники.

Отношение длинной стороны первого прямоугольника к короткой будет 0,7. Это почти 0,68 в Золотом сечении.

Кубирование куба

«Кубирование куба», то есть разбиение куба на конечное число попарно неравных между собой кубов, невозможно. Доказательство этого факта было дано Бруксом, Смитом, Стоуном и Таттом.

Доказательство

Допустим, что искомое разбиение куба существует.

Рассмотрим одну из граней куба, очевидно, не уменьшая общность, можно выбрать нижнюю грань.

На нижней грани стоят разновеликие кубы, своими нижними рёбрами разбивающие грань на разновеликие квадраты.

Найдём самый маленький квадрат разбиения нижней грани. Очевидно, что этот квадрат не может примыкать к ребру куба, будучи ограничен сторонами бо́льших квадратов, следовательно, он должен располагаться где-то внутри грани.

Теперь рассмотрим верхнюю грань этого малого кубика. Поскольку по предположению это самый маленький кубик на нижней грани куба, он окружен более высокими кубами. Поэтому на его верхнюю грань не заступает ни один соседний куб. Следовательно, стоящие на этой грани кубики меньшего размера снова разбивают верхнюю грань этого кубика на разновеликие квадраты, причём самый малый квадрат разбиения верхней грани рассматриваемого кубика снова не может принадлежать ребру кубика и находится внутри грани.

Продолжая этот процесс рассуждения, приходим к противоречию, что доказывает теорему.

Гиперкубирование гиперкуба

Также легко доказывается теорема о невозможности «гиперкубирования гиперкуба» для гиперкубов любой размерности, большей 3-х. Действительно, для любой размерности n гиперкубы разбиения, прилегающие к какой-либо (n − 1)-мерной гиперграни исходного гиперкуба, должны разбивать эту гипергрань на конечное число попарно неравных (n − 1)-мерных гиперкубов. При n = 4 «гиперкубирование» невозможно, так как должно порождать «кубирование» 3-мерных гиперграней исходного 4-мерного гиперкуба. Индукцией по n можно сделать заключение о невозможности «гиперкубирования» для всех n > 3.

Уравнение квадрата

При необходимости вычислить значение различных величин у квадрата (площади, периметра, длин сторон или диагоналей) используют различные уравнения, которые выводятся из свойств квадрата, основных законов и правил геометрии.

1. Уравнение площади квадрата

Из уравнений для вычисления площади четырехугольников мы знаем, что она (площадь) равна произведению длины и ширины. А так как стороны квадрата одинаковые по длине, то площадь его будет равна длине любой стороны, возведенной во вторую степень

S=a2.

Используя теорему Пифагора, мы можем вычислить площадь квадрата, зная длину его диагонали.

S=d2/2.

2. Уравнение периметра квадрата

Периметр квадрата, как и всех четырехугольников, равен сумме длин его сторон, а так как они все одинаковые, то можно сказать, что периметр квадрата равен длине стороны, умноженной на четыре

P=a+a+a+a=4a.

Снова теорема Пифагора поможет нам найти периметр через диагональ. Нужно значение длины диагонали умножить на два корня из двух

P=2√2d

3. Уравнение диагонали квадрата

Диагонали квадрата равны, пересекаются под прямым углом и делятся точкой пересечения пополам.

Найти их можно, исходя из вышеприведенных уравнений площади и периметра квадрата

d=√2*a, d=√2S, d=P/2√2

Есть еще способы узнать, какова же длина диагонали квадрата. Радиус вписанной в квадрат окружности равен половине его диагонали, отсюда

d=√2D=2√2R, где D — диаметр, а R — радиус вписанной окружности.

Зная радиус описанной окружности, рассчитать диагональ еще проще, ведь она является диаметром, то есть d=D=2R.

Но не стоит забывать, что квадрат — это участок плоскости, ограниченный четырьмя пересекающимися линиями.

Для линий (и образованных ими фигур) существует достаточно уравнений, не нуждающихся в дополнительном описании, но линия бесконечна. А многоугольники ограничены пересечением линий. Для них можно использовать линейные уравнения, объединенные в систему, задающие прямые линии. Но необходимо указывать дополнительные параметры, условия.

Для определения многоугольников же необходимо составить такое уравнение, которое бы описывало не линию, а отдельный произвольный отрезок без вмешательства дополнительных условий и описаний.

[ x/x_i ]*[ x_i/x]*y_i — вот это специальное уравнение для многоугольников.

Квадратные скобки в нем указывают на условие исключения дробной части числа, то есть мы должны оставить только целое число. y_i — функция, которая выполнятся в диапазоне параметра от x до x_i.

Используя это уравнение, можно вывести новые уравнения для вычисления отрезков и линий, состоящих из нескольких отрезков. Оно является базовым, универсальным для многоугольников.

Помним, что квадрат — это часть плоскости, поэтому его описание типа y=f(x) можно представить, чаще всего, только как многозначную функцию, которую, в свою очередь, можно выразить через однозначные, если представлять их параметрически, то есть зависящими от какого-либо параметра t:

x=f(t), y=f(t).

Так вот, если использовать в совокупности универсальное уравнение и параметрическое представление, то действительно можно вывести уравнение для выражения многоугольников:

x=((A2+A3)*A5+A4*P)*Cos(L)

y=((A1+A4)*A5+A3*P)*Sin(L),

где

A1=[1/[T/P]]*[T/P]; A2=[2/[T/P]]*[[T/P]/2]; A3=[3/[T/P]]*[[T/P]/3]; A4=[4/[T/P]]*[[T/P]/4]; A5=T-P*[T/P],

где P — диагональ прямоугольника, L — угол наклона к горизонтали диагонали P, T — параметр изменяющийся в диапазоне от P до 5P.

Если L=3,14/4, то уравнение будет описывать квадраты разной величины, в зависимости от размера диагонали P.

Расчет угла Ганна для среднесрочной торговли

В своих трудах Уильям Ганн писал, что различные торговые инструменты двигаются по-разному и имеют свои особенности, но, как правило, все они стремятся к какому-то определенному значению. Если рассматривать этот факт с точки зрения «Квадрата 9», то можно заметить, что цены и даты разворотных точек располагаются вдоль определенного угла на «колесе», иногда возникает ситуация, когда таких углов два.

Рассмотрим конкретную ситуацию на примере. Допустим, на рынке наблюдалось какое-то нисходящее движение, которое сменилось трендом вверх. Мы отмечаем на графике четыре точки, которые обозначают первую вибрацию в начале движения. У этих точек есть абсциссы, которые характеризуют время, когда это произошло, и ординаты, характеризующие цену. Именно благодаря этим восьми числам мы будем рассчитывать то, что будет происходить с рынком в будущем. Для удобства пронумеруем эти точки от 1 до 4. Как правило, точка 1 играет роль начала координат, точка 2 отвечает за ориентацию колеса, а точки 3 и 4 отвечают за наличие определенного угла. Затем вы строите квадрат Ганна и отмечаете на нем четыре точки – первая точка отмечается в центре, вторая точка больше, чем первая, располагается примерно в 21 ячейке, третья точка находится ниже второй, но выше первой, поэтому она размещается в ячейку 18, а четвертая точка выше второй и всех остальных точек, поэтому располагается в ячейке 27. Далее нужно ориентировать «колесо» по центру 21 ячейки следующим образом:

После этого необходимо подобрать фигуру наложения, которая пройдет через точку 3 или 4. В нашем примере это будет простая фигура – треугольник. Если ни одна фигура не проходит ни через одну точку, значит точки были определены неправильно.