Исследовательская работа по математике «приемы устных вычислений»

Основные направления

В вычислительной математике выделяют следующие направления: анализ математических моделей, разработка методов и алгоритмов решения стандартных математических задач, автоматизация программирования.

Анализ выбранных математических моделей для поставленной задачи начинается с анализа и обработки входной информации, что очень важно для более точных входных данных. Для такой обработки зачастую применяются методы математической статистики

Следующим шагом является численное решение математических задач и анализ результатов вычислений. Степень достоверности результатов анализа должна соответствовать точности входных данных. Появление более точных входных данных может потребовать усовершенствования построенной модели или даже её замены.

Методы и алгоритмы решения типовых математических задач с применением вычислительной техники носят название численных методов. К типовым задачам относят:

• Алгебра: решение систем линейных уравнений, обращение матриц, поиск собственных значений и векторов матриц (ограниченная и полная проблема собственных значений), поиск сингулярных значений и векторов матриц, решение нелинейных алгебраических уравнений, решение систем нелинейных алгебраических уравнений;
• Дифференциальные уравнения: дифференцирование и интегрирование функций одного или нескольких переменных, решение обыкновенных дифференциальных уравнений, решение уравнений с частными производными, решение систем дифференциальных уравнений, решение интегральных уравнений;
• Оптимизация: изучение минимальных и максимальных значений функционалов на множествах;
• Исследование операций и теория игр: минимаксные задачи (в частности, для многошаговых игр);
• математическое программирование: задачи аппроксимации, задачи интерполяции, задачи экстраполяции.

Проводится изучение и сравнительный анализ методов решения типовых задач. Важным элементом анализа является поиск экономичных моделей, позволяющих получить результат, используя наименьшее число операций, оптимизация методов решения. Для задач больших размеров особенно важным является исследование устойчивости методов и алгоритмов, в том числе к ошибкам округления. Примерами неустойчивых задач является обратные задачи (в частности, поиск обратной матрицы), а также автоматизация обработки результатов экспериментов.

Постоянно увеличивающийся круг типовых задач и рост числа пользователей определили повышение требований к автоматизации. В условиях, когда знание конкретных численных методов является несущественным для пользователя, возрастают требования к стандартным программам решения. С их использованием не требуется программирование методов решения, а достаточно задать исходную информацию.

Презентация на тему: » Практические приемы приближенных вычислений. А-8 урок 1.» — Транскрипт:

1

Практические приемы приближенных вычислений. А-8 урок 1

2

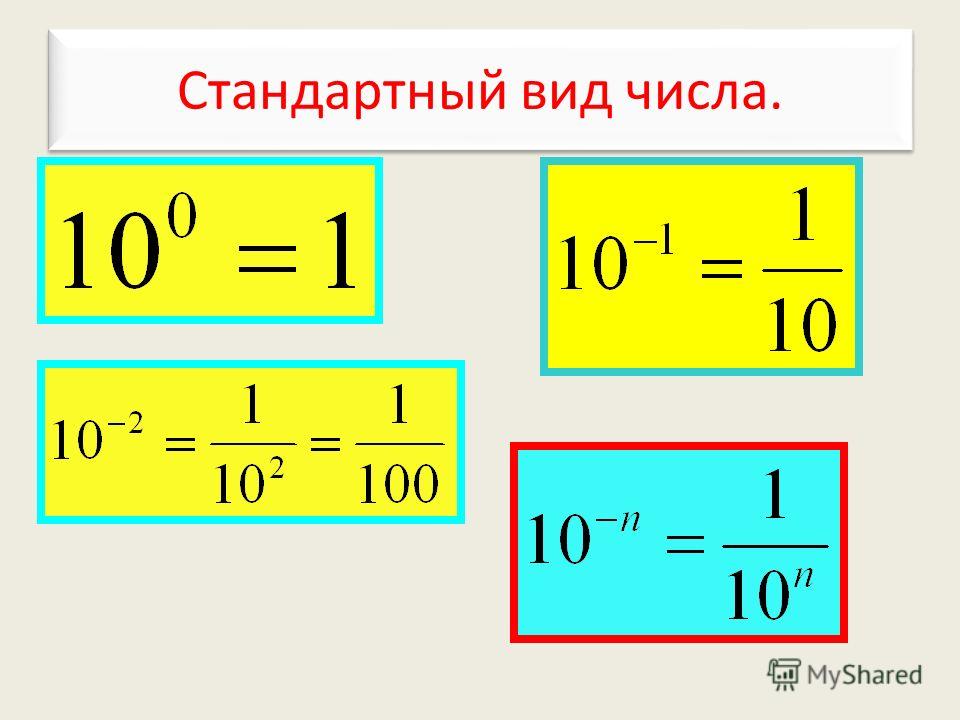
Стандартный вид числа. Стандартный вид числа.

3

Если с – натуральное число или положительная конечная десятичная дробь, то представление этого числа в виде с = а10 n где 1а ˂ 10, k-целое число, называют записью числа в стандартном виде. а- мантисса числа k-порядок числа с Если с – натуральное число или положительная конечная десятичная дробь, то представление этого числа в виде с = а10 n где 1а ˂ 10, k-целое число, называют записью числа в стандартном виде. а- мантисса числа k-порядок числа с Стандартный вид числа. Стандартный вид числа.

4

520=5, ,0054=5, =2, =1, =5, ,0054=5, =2, =1, Стандартный вид числа. Стандартный вид числа.

5

Назовите правильную запись числа в стандартном виде: 0, =

6

Назовите правильную запись числа в стандартном виде: 0, =

7

Назовите правильную запись числа в стандартном виде: =

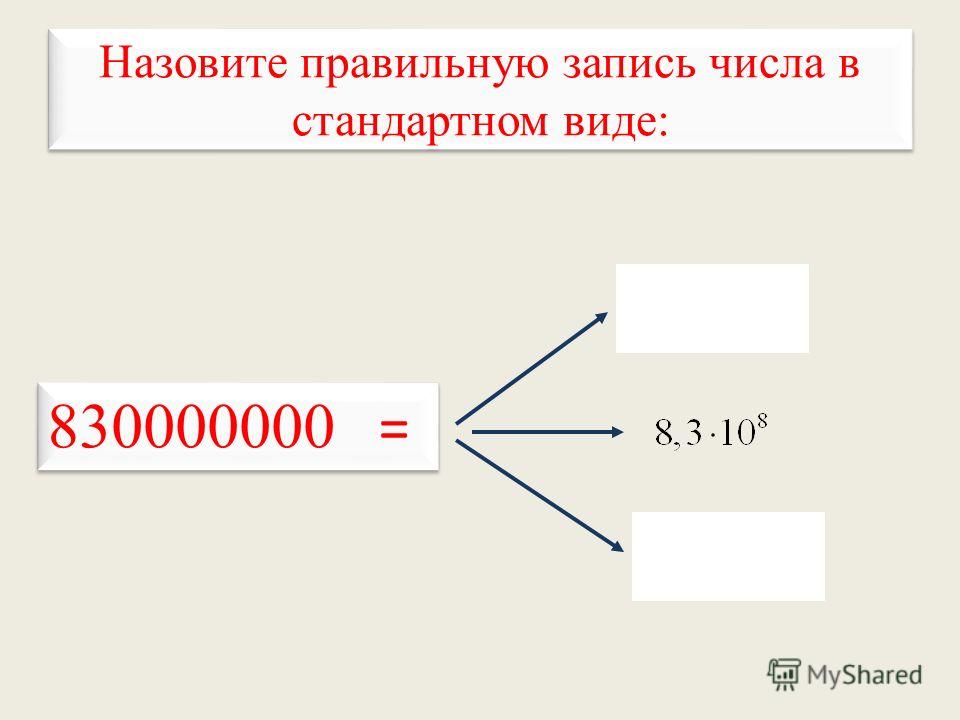
8

Назовите правильную запись числа в стандартном виде: =

9

Назовите число, записанное в стандартном виде: Правильный ответ Правильный ответ

10

Верные и сомнительные цифры Цифру какого-либо разряда в записи приближенного значения называют верной, если граница абсолютной погрешности не превосходит единицы этого разряда. В противном случае цифру называют сомнительной. Если граница абсолютной погрешности не превосходит половины единицы разряда, следующего за разрядом рассматриваемой цифры, то эту цифру в записи приближенного значения числа называют строго верной. Если граница абсолютной погрешности не превосходит половины единицы разряда, следующего за разрядом рассматриваемой цифры, то эту цифру в записи приближенного значения числа называют строго верной.

11

239(2,4,6) 240 (2,4,6)

12

Сложение и вычитание приближенных значений. х = а + h 1 y = b + h 2 х + y = (а + b) + (h 1 + h 2 ) x — y = (а — b) + (h 1 + h 2 )

13

При сложении и вычитании приближенных значений, в записи которых все цифры верные, в сумме и в разности оставляют столько десятичных знаков, сколько их имеет приближенное значение с наименьшим числом десятичных знаков.

14

241(2,4,6)

15

Умножение и деление приближенных значений. Значащими цифрами называются все верные цифры в десятичной записи приближенного значения, кроме нулей, стоящих перед первой отличной от нуля цифрой. 0, ,00350

16

Умножение и деление приближенных значений. При умножении и делении приближенных значений в произведении и частном оставляют столько цифр ( не считая нулей, отличной от нуля цифрой), сколько значащих цифр имеет приближенное значение с меньшим числом значащих цифр.

Значащие цифры

Если абсолютная
погрешность величины a не превышает одной
единицы разряда последней цифры числа a, то
говорят, что у числа все знаки верные.

Приближенные числа следует
записывать, сохраняя только верные знаки. Если,
например, абсолютная погрешность числа 52400 равна
100, то это число должно быть записано, например, в
виде 524 .102 или 0,524 .105.
Оценить погрешность приближенного числа можно,
указав, сколько верных значащих цифр оно
содержит. При подсчете значащих цифр не
считаются нули с левой стороны числа.

Примеры:

	1 куб.фут = 0.0283 м3 — три верных значащих цифры
	1 дюйм = 2,5400 v пять верных значащих цифр.

Если число aимеет nверных
значащих цифр, то его относительная погрешность d_a

T 1/(z*dn-1),
где z — первая значащая цифра числa a; d — основание
системы счисления.

У числаa
с относительной погрешностьюd_a верныn значащих цифр, где n — наибольшее целое число,
удовлетворяющее неравенству (1+Z)d_a T dl-n.

Пример:

Если число a = 47,542
получено в результате действий над
приближенными числами и известно, что d_a = 0,1%, то a
имеет 3 верных знака, так как (4+1)0,001 T 10v2.

Урок 28. Нахождение приближенных значений квадратного корня

Содержание (быстрый переход):

Цель: сформировать представление о приближенном вычислении квадратного корня.Планируемые результаты: научиться вычислять приближенное значение корня из числа.Тип урока: урок–исследование.

Ход урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Решите уравнение: а) x2 – 0,04 = 0,6; б) (2х – З)2 = 16;    в) (3х + а)2 = 81.
2. Определите число корней уравнения x2 – 4х = а.

Вариант 2

1. Решите уравнение: а) x2 + 0,05 = 0,3; б) (Зх + 2)2 = 36;    в) (2х – а)2 = 49.
2. Определите число корней уравнения –x2 + 6х = а.

III. Работа по теме урока

На предыдущих занятиях мы узнали, что √a может быть целым числом (например, √0 = 0, √9 = 3 и т. д.), обыкновенной дробью (например,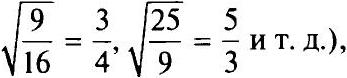 

десятичной дробью (например,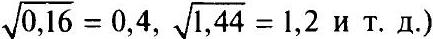 

и иррациональным числом (например, 

Так как иррациональное число является бесконечной десятичной непериодической дробью, то при практических вычислениях возникает вопрос о вычислении приближенного значения арифметического квадратного корня.

Пример 1. Найдем приближенное значение √3 с двумя знаками после запятой.

Оценим подкоренное выражение 3 сначала в целых числах. Так как 1 < 3 < 4, то √1 < √3 < √4 или 1 < √3 < 2. Поэтому десятичная запись числа √З начинается с цифры 1, т. е. √3 ≈ 1,… (рис. а).

Найдем теперь цифру десятых. Для этого будем возводить в квадрат десятичные дроби 1,1; 1,2; 1,3… до тех пор, пока вновь не оценим такими числами подкоренное выражение 3. Имеем 1,12 = 1,21; 1,22 = 1,44; 1,32 = 1,69; 1,42 = 1,96; 1,52 = 2,25; 1,62 = 2,56; 1,72 = 2,89; 1,82 = 3,24. Так как 2,89 < 3 < 3,24 или 1,72 < 3 < 1,82, то 1,7 < √З < 1,8. Значит, √3 ≈ 1,7… (рис. б).

Чтобы найти цифру сотых, будем последовательно возводить в квадрат десятичные дроби 1,71; 1,72; 1,73…, вновь оценивая подкоренное выражение 3. Имеем: 1,712 = 2,9241; 1,722 = 2,9584; 1,732 = 2,9929; 1,742 = 3,0276. Так как 1,732 < 3 < 1,742, то 1,73 < √3 < 1,74 (рис. в). Поэтому √3 ≈ 1,73.

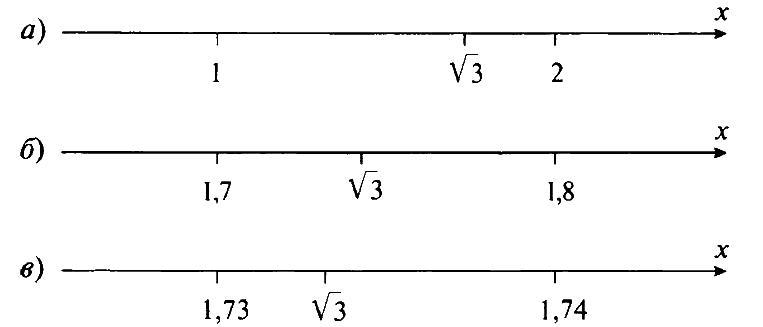
Аналогичным образом можно найти приближенное значение арифметического квадратного корня с любой заданной точностью.

При практических расчетах для нахождения приближенных значений квадратных корней используют специальные таблицы или вычислительную технику.

Пример 2. С помощью калькулятора найдем .

Введем в калькулятор число 27,4 и нажмем клавишу √. На экране появится число 5,234500931 — приближенное значение . Полученный результат округляют до требуемого количества знаков. Округлим, например, этот результат до сотых и получим  ≈ 5,23.

V. Подведение итогов урока

Домашнее задание: № 336 (в, е); 338 (а); 339 (б); 340 (а); 344 (в, г); 345 (б); 348 (а, в).

Вы смотрели: Поурочное планирование по алгебре для 8 класса. УМК Макарычев (Просвещение). Глава 2. КВАДРАТНЫЕ КОРНИ (19 ч). § 5. Арифметический квадратный корень (5 ч). Урок 28. Нахождение приближенных значений квадратного корня.

Вернуться к Списку уроков Тематического планирования.

Основные направления

В вычислительной математике выделяют следующие направления: анализ математических моделей, разработка методов и алгоритмов решения стандартных математических задач, автоматизация программирования.

Анализ выбранных математических моделей для поставленной задачи начинается с анализа и обработки входной информации, что очень важно для более точных входных данных. Для такой обработки зачастую применяются методы математической статистики

Следующим шагом является численное решение математических задач и анализ результатов вычислений. Степень достоверности результатов анализа должна соответствовать точности входных данных. Появление более точных входных данных может потребовать усовершенствования построенной модели или даже её замены.

Методы и алгоритмы решения типовых математических задач с применением вычислительной техники носят название численных методов. К типовым задачам относят:

• Алгебра: решение систем линейных уравнений, обращение матриц, поиск собственных значений и векторов матриц (ограниченная и полная проблема собственных значений), поиск сингулярных значений и векторов матриц, решение нелинейных алгебраических уравнений, решение систем нелинейных алгебраических уравнений;
• Дифференциальные уравнения: дифференцирование и интегрирование функций одного или нескольких переменных, решение обыкновенных дифференциальных уравнений, решение уравнений с частными производными, решение систем дифференциальных уравнений, решение интегральных уравнений;
• Оптимизация: изучение минимальных и максимальных значений функционалов на множествах;
• Исследование операций и теория игр: минимаксные задачи (в частности, для многошаговых игр);
• математическое программирование: задачи аппроксимации, задачи интерполяции, задачи экстраполяции.

Проводится изучение и сравнительный анализ методов решения типовых задач. Важным элементом анализа является поиск экономичных моделей, позволяющих получить результат, используя наименьшее число операций, оптимизация методов решения. Для задач больших размеров особенно важным является исследование устойчивости методов и алгоритмов, в том числе к ошибкам округления. Примерами неустойчивых задач является обратные задачи (в частности, поиск обратной матрицы), а также автоматизация обработки результатов экспериментов.

Постоянно увеличивающийся круг типовых задач и рост числа пользователей определили повышение требований к автоматизации. В условиях, когда знание конкретных численных методов является несущественным для пользователя, возрастают требования к стандартным программам решения. С их использованием не требуется программирование методов решения, а достаточно задать исходную информацию.

Приближенные вычисления

Приближенные вычисления можно рассматривать как одно из примененийпроизводной, а конкретно касательной данной функции. С приближениями мы встречаемся довольно часто, например, если нужно какие-то значения числа , то пишем , и т. д.

Рассмотрим общий прием получения с хорошей точностью приближенных значений. Предположим, что задана функция и эта функция имеет сложный график. Достаточно задать точку , для того чтобы получить касательную. Проведем в точке касательную. Запишем уравнение этой касательной . В окрестности точки график касательной и график данной функции почти не отличаются (см. рис.1). Предположим, что приращение аргумента невелико. Имеем — точное значение функции в точке . Приближенное значение дает касательная, и если невелико, то , то есть значение функции в новой точке мало отличается от значения линейной функции (касательной).

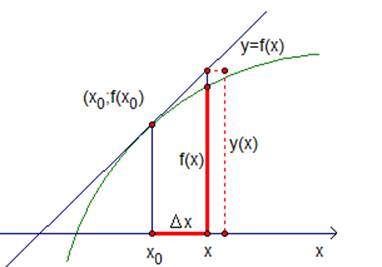
Рис. 1. График функции и касательная.

Итак, идея простая и ясная: в хорошей точки ( хорошая означает то, что в этой точке легко вычислить значение функции) легко вычислить значение . Если в точке легко вычислить значение , то в новой точке заменим значение на значение , то есть кривую заменим касательной. Получим примерный результат. Этот результат будет тем точнее, чем меньше будет приращение .

Например, вычислить приближенно величину (решение ниже).

Вычислить приближенно .

Сделаем иллюстрацию (см. рис.2).

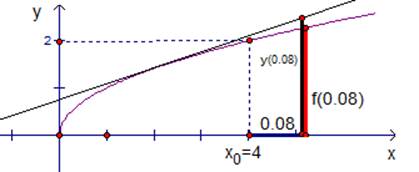
Рис. 2. График функции .

, а . . Заменим значение функции в точке значением касательной .

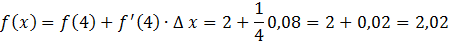
; ; . Итак, .

Таким образом, приближенные вычисления основываются на уравнении касательной. Методику применения мы рассмотрели на конкретном примере.

Особенности представления чисел в компьютере

Основное отличие вычислительной математики заключается в том, что при решении вычислительных задач человек оперирует машинными числами, которые являются дискретной проекцией вещественных чисел на конкретную архитектуру компьютера. Так, например, если взять машинное число длиной в 8 байт (64 бита), то в нём можно запомнить только 264 разных чисел, поэтому важную роль в вычислительной математике играют оценки точности алгоритмов и их устойчивость к представлениям машинных чисел в компьютере. Именно поэтому, например, для решения линейной системы алгебраических уравнений очень редко используется вычисление обратной матрицы, так как этот метод может привести к ошибочному решению в случае с сингулярной матрицей, а очень распространённый в линейной алгебре метод, основанный на вычислении определителя матрицы и её дополнения, требует гораздо больше арифметических операций, чем любой устойчивый метод решения линейной системы уравнений.

1. Приближенные вычисления

При­бли­жен­ные вы­чис­ле­ния можно рас­смат­ри­вать как одно из при­ме­не­ний про­из­вод­ной, а кон­крет­но ка­са­тель­ной дан­ной функ­ции. С при­бли­же­ни­я­ми мы встре­ча­ем­ся до­воль­но часто, на­при­мер, если нужно ка­кие-то зна­че­ния числа , то пишем ,  и т. д.

Рас­смот­рим общий прием по­лу­че­ния с хо­ро­шей точ­но­стью при­бли­жен­ных зна­че­ний. Пред­по­ло­жим, что за­да­на функ­ция   и эта функ­ция имеет слож­ный гра­фик. До­ста­точ­но за­дать точку , для того чтобы по­лу­чить ка­са­тель­ную. Про­ве­дем в точке  ка­са­тель­ную. За­пи­шем урав­не­ние этой ка­са­тель­ной . В окрест­но­сти точки  гра­фик ка­са­тель­ной и гра­фик дан­ной функ­ции почти не от­ли­ча­ют­ся (см. рис.1). Пред­по­ло­жим, что при­ра­ще­ние ар­гу­мен­та  неве­ли­ко. Имеем  — точ­ное зна­че­ние функ­ции в точке . При­бли­жен­ное зна­че­ние  дает ка­са­тель­ная, и если   неве­ли­ко, то , то есть зна­че­ние функ­ции в новой точке мало от­ли­ча­ет­ся от зна­че­ния ли­ней­ной функ­ции (ка­са­тель­ной).

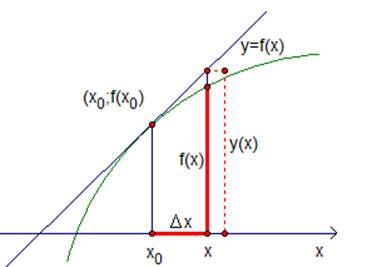
Рис. 1. Гра­фик функ­ции  и ка­са­тель­ная.

Итак, идея про­стая и ясная: в хо­ро­шей точки ( хо­ро­шая озна­ча­ет то, что в этой точке легко вы­чис­лить зна­че­ние функ­ции) легко вы­чис­лить зна­че­ние . Если в точке  легко вы­чис­лить зна­че­ние , то в новой точке  за­ме­ним зна­че­ние  на зна­че­ние , то есть кри­вую за­ме­ним ка­са­тель­ной. По­лу­чим при­мер­ный ре­зуль­тат. Этот ре­зуль­тат будет тем точ­нее, чем мень­ше будет при­ра­ще­ние .

На­при­мер, вы­чис­лить при­бли­жен­но ве­ли­чи­ну  (ре­ше­ние ниже).

Вы­чис­лить при­бли­жен­но .

Сде­ла­ем ил­лю­стра­цию (см. рис.2).

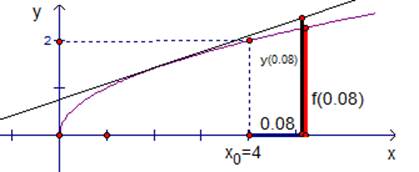
Рис. 2. Гра­фик функ­ции .

, а . . За­ме­ним зна­че­ние функ­ции в точке  зна­че­ни­ем ка­са­тель­ной .

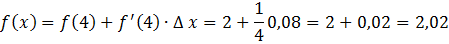
; ; . Итак, .

Таким об­ра­зом, при­бли­жен­ные вы­чис­ле­ния ос­но­вы­ва­ют­ся на урав­не­нии ка­са­тель­ной. Ме­то­ди­ку при­ме­не­ния мы рас­смот­ре­ли на кон­крет­ном при­ме­ре.

Особенности представления чисел в компьютере

Основное отличие вычислительной математики заключается в том, что при решении вычислительных задач человек оперирует машинными числами, которые являются дискретной проекцией вещественных чисел на конкретную архитектуру компьютера. Так, например, если взять машинное число длиной в 8 байт (64 бита), то в нём можно запомнить только 264 разных чисел, поэтому важную роль в вычислительной математике играют оценки точности алгоритмов и их устойчивость к представлениям машинных чисел в компьютере. Именно поэтому, например, для решения линейной системы алгебраических уравнений очень редко используется вычисление обратной матрицы, так как этот метод может привести к ошибочному решению в случае с сингулярной матрицей, а очень распространённый в линейной алгебре метод, основанный на вычислении определителя матрицы и её дополнения, требует гораздо больше арифметических операций, чем любой устойчивый метод решения линейной системы уравнений.

12.2. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

При многократном измерении одной и той же величины каждый раз получают несколько отличающиеся результаты, как по абсолютной величине, так и по знакам, каким бы опытом не обладал исполнитель и какими бы высокоточными приборами он не пользовался.
Погрешности различают: грубые, систематические и случайные.
Появление грубых погрешностей (промахов) связано с серьезными ошибками при производстве измерительных работ. Эти ошибки легко выявляются и устраняются в результате контроля измерений.Систематические погрешностивходят в каждый результат измерений по строго определенному закону. Они обусловлены влиянием конструкции измерительных приборов, погрешностями градуировки их шкал, износом и т. д. (инструментальные погрешности)иливозникают из-за недоучета условий измерений и закономерностей их изменений, приближенности некоторых формул и др. (методические погрешности). Систематические погрешности делятся на постоянные (неизменные по знаку и вели чине) и переменные (изменяющие свою величину от одного измерения к другому по определенному закону).
Такие погрешности заранее определимы и могут быть сведены к необходимому минимуму путем введения соответствующих поправок.Например, заранее может быть учтено влияние кривизны Земли на точность определения вертикальных расстояний, влияние температуры воздуха и атмосферного давления при определении длин линий светодальномерами или электронными тахеометрами, заранее можно учесть влияние рефракции атмосферы и т. д.
Если не допускать грубых погрешностей и устранять систематические, то качество измерений будет определяться только случайными погрешностями. Эти погрешности неустранимы, однако их поведение подчиняется законам больших чисел. Их можно анализировать, контролировать и сводить к необходимому минимуму.
Для уменьшения влияния случайных погрешностей на результаты измерений прибегают к многократным измерениям, к улучшению условий работы, выбирают более совершенные приборы, методы измерений и осуществляют тщательное их производство.
Сопоставляя ряды случайных погрешностей равноточных измерений можно обнаружить, что они обладают следующими свойствами:
а) для данного вида и условий измерений случайные погрешности не могут превышать по абсолютной величине некоторого предела;
б) малые по абсолютной величине погрешности появляются чаще больших;
в) положительные погрешности появляются так же часто, как и равные им по абсолютной величине отрицательные;
г) среднее арифметическое из случайных погрешностей одной и той же величины стремится к нулю при неограниченном увеличении числа измерений.
Распределение ошибок, соответствующее указанным свойствам, называется нормальным (рис. 12.1).

Рис. 12.1. Кривая нормального распределения случайных погрешностей Гаусса

Разность между результатом измерения некоторой величины (l) и ее истинным значением (X) называют абсолютной (истинной) погрешностью.

Δ = l — X

Истинное (абсолютно точное) значение измеряемой величины получить невозможно, даже используя приборы самой высокой точности и самую совершенную методику измерений. Лишь в отдельных случаях может быть известно теоретическое значение величины. Накопление погрешностей приводит к образованию расхождений между результатами измерений и действительными их значениями.Разность суммы практически измеренных (или вычисленных) величин и теоретического ее значения называется невязкой. Например, теоретическая сумма углов в плоском треугольнике равна 180º, а сумма измеренных углов оказалась равной 180º02′; тогда погрешность суммы измеренных углов составит +0º02′. Эта погрешность будет угловой невязкой треугольника.
Абсолютная погрешность не является, полным показателем точности выполненных работ. Например, если некоторая линия, фактическая длина которой составляет 1000 м, измерена землемерной лентой с ошибкой 0,5 м, а отрезок длиною 200 м  – с ошибкой 0,2 м, то, несмотря на то, что абсолютная погрешность первого измерения больше второго, все же первое измерение было выполнено с точностью в два раза более высокой. Поэтому вводят понятие относительной погрешности:

Отношение абсолютной погрешности измеряемой величины Δ к измеренной величине l называют относительной погрешностью.

Относительные погрешности всегда выражаются дробью с числителем, равным единице (аликвотная дробь). Так, в приведенном выше примере относительная погрешность первого измерения составляет

,

а второго 

.

Программное обеспечение

Численное моделирование аварии автомобиля

Алгоритмы решения множества стандартных задач вычислительной математики реализованы на различных языках программирования. Чаще всего для этих целей используются языки Julia, Фортран и C, библиотеки для которых можно найти в репозитории Netlib (англ.)русск.. Кроме того, большую популярность имеют коммерческие библиотеки IMSL (англ.)русск. и NAG (англ.)русск., а также свободная GNU Scientific Library.

Программные пакеты MATLAB, Mathematica, Maple, S-PLUS (англ.)русск., LabVIEW и IDL (англ.)русск., а также их свободные альтернативы FreeMat, Scilab, GNU Octave (похожа на Matlab), IT++ (англ.)русск. (библиотека C++), R (похож на S-PLUS) имеет различные численные методы, а также средства для визуализации и отображения результатов.

Многие системы компьютерной алгебры, такие как Mathematica, имеют возможность задавать необходимую арифметическую точность, что позволяет получить результаты более высокой точности. Также большинство электронных таблиц могут быть использованы для решения простых задач вычислительной математики.

Действия над приближенными числами

Результат действий над
приближёнными числами представляет собой также
приближённое число. Погрешность результата
может быть выражена через погрешности
первоначальных данных при помощи следующих
теорем:

1. Предельная
   абсолютная погрешность алгебраической суммы
   равна сумме предельных абсолютных погрешностей
   слагаемых.

2. Относительная
   погрешность суммы заключена между наибольшей и
   наименьшей из относительных погрешностей
   слагаемых.

3. Относительная
   погрешность произведения или частного равна
   сумме относительных погрешностей сомножителей
   или, соответственно, делимого и делителя.

4. Относительная
   погрешность n-ой степени приближенного числа в n
   раз больше относительной погрешности основания
   (как у целых, так и для дробных n).

Пользуясь этими
теоремами, можно определить погрешность
результата любой комбинации арифметических
действий над приближенными числами.

Примеры:

V = r2hD_v = Vd _v = V(2d _r+d
_n)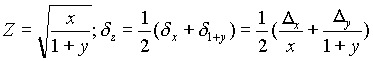

Предельная абсолютная
погрешность заведомо превосходит абсолютную
величину истинной погрешности, поскольку
предельное значение вычисляется в
предположения, что различные погрешности
усиливают друг друга; практически это бывает
редко. При массовых вычислениях, когда не
учитывают погрешность каждого отдельного
результата, пользуются следующими правилами
подсчета цифр.

При соблюдении этих
правил можно считать, что в среднем полученные
результаты будут иметь все знаки верными, хотя в
отдельных случаях возможна ошибка в несколько
единиц последнего знака.

1. При сложении и
   вычитании приближённых чисел в результате
   следует сохранять столько десятичных знаков,
   сколько их в приближённом данном с наименьшим
   числом десятичных знаков.

2. При умножении и
   делении в результате следует сохранять столько
   значащих цифр, сколько их имеет приближённое
   данное с наименьшим числом значащих цифр.

3. При возведении в
   квадрат или куб в результате следует сохранять
   столько значащих цифр, сколько их имеет
   возводимое в степень приближённое число (
   последняяцифра квадрата и особенно куба
   при этом менее надежна, чем последняя цифра
   основания ).

4. При увеличении
   квадратного и кубического корней в результате
   следует брать столько значащих цифр, сколько их
   имеет приближённое значение подкоренного числа
   (последняя цифра квадратного и особенно
   кубического корня при этом более надёжна, чем
   последняя цифра подкоренного числа).

5. Во всех промежуточных
   результатах следует сохранять одной цифрой
   более, чем рекомендуют предыдущие правила. В
   окончательном результате эта ?запасная¦ цифра
   отбрасывается.

6. Если некоторые данные
   имеют больше десятичных знаков (при сложении и
   вычитании) или больше значащих цифр (при
   умножении, делении, возведении в степень,
   извлечении корня), чем другие, то их
   предварительно следует округлить, сохраняя лишь
   одну лишнюю цифру.

Если данные можно брать с
произвольной точностью, то для получения
результата с K цифрами данные следует брать
с таким числом цифр, какое даёт согласно правилам
1-4(К+1) цифру в результате.

Назад | | Вперед

Источники погрешностей

Рассмотрим различные причины возникновения погрешностей.

Математическая модель задачи является неточной

Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций).

Ошибки в исходных данных

Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения.

Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений.

Вычислительные ошибки (ошибки округления)

Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы.

Погрешности

Разница между точным числом x
и его приближенным значением a называется погрешностью
данного приближенного числа. Если известно, что |
x — a | < D_a,
то величина D_a
называется предельной абсолютной
погрешностью приближенной величины a.

Отношение D_a / a = d_a
называется предельной относительной
погрешностью; последнюю часто выражают в
процентах.

Пример:

3,14 является
приближенным значением числа p, погрешность его равна
0,00159…, предельную абсолютную погрешность можно
считать равной 0,0016, а предельную относительную
погрешность v равной 0.0016/3.14 = 0,00051 = 0,051%. Для
краткости обычно слово ?предельная¦
опускается.

2. Вывод формулы для приближенных вычислений

Рас­смот­рим фор­му­лы для при­бли­жен­ных вы­чис­ле­ний для функ­ции  в окрест­но­сти точки , то есть в точке  (см. рис.3).

Рис. 3. Окрест­ность точки  .

Зна­че­ние функ­ции в точке  равно . До­ка­зать, что .

До­ка­за­тель­ство.

За­ме­ним функ­цию ка­са­тель­ной.

; ; . Если за­ме­ним зна­че­ние функ­ции зна­че­ни­ем ка­са­тель­ной, то по­лу­чим .

По­лу­чи­ли фор­му­лу, ко­то­рая поз­во­ля­ет при­мер­но, с до­ста­точ­ной сте­пе­нью точ­но­сти, вы­чис­лять нуж­ные зна­че­ния.

При­ме­ним эту фор­му­лу для ре­ше­ния при­ме­ра, ко­то­рый был дан вна­ча­ле: найти при­бли­жен­ное зна­че­ние .

Рис. 4. При­ра­ще­ние ар­гу­мен­та.

Вы­чис­лим при­ра­ще­ние  (см. рис.4). От­сю­да,

.

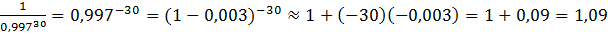Если осо­бая точ­ность не нужна, то такое при­мер­ное вы­чис­ле­ние до­воль­но эф­фек­тив­но.

Вывод формулы для приближенных вычислений

Рассмотрим формулы для приближенных вычислений для функции в окрестности точки , то есть в точке (см. рис.3).

Рис. 3. Окрестность точки .

Значение функции в точке равно . Доказать, что .

Доказательство.

Заменим функцию касательной.

; ; . Если заменим значение функции значением касательной, то получим .

Получили формулу, которая позволяет примерно, с достаточной степенью точности, вычислять нужные значения.

Применим эту формулу для решения примера, который был дан вначале: найти приближенное значение .

Рис. 4. Приращение аргумента.

Вычислим приращение (см. рис.4). Отсюда,

.

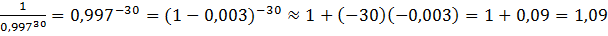Если особая точность не нужна, то такое примерное вычисление довольно эффективно.