Уровни фибоначчи: как можно их использовать в трейдинге?

В других областях

Существует мнение, что почти все утверждения, находящие числа Фибоначчи в природных и исторических явлениях, неверны — это распространённый миф, который часто оказывается неточной подгонкой под желаемый результат.

В природе

• Филлотаксис (листорасположение) у растений описывается последовательностью Фибоначчи. Семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи
• Длины фаланг пальцев человека относятся примерно как числа Фибоначчи.
• Раковины моллюсков, в частности Наутилуса, строятся по спирали, соотносящейся[как?] с рядом чисел Фибоначчи.[источник не указан 892 дня]

What Do Fibonacci Numbers and Lines Tell You?

Some traders believe that the Fibonacci numbers play an important role in finance. As discussed above, the Fibonacci number sequence can be used to create ratios or percentages that traders use.

These include: 23.6%, 38.2%, 50% 61.8%, 78.6%, 100%, 161.8%, 261.8%, 423.6%.

These percentages are applied using many different techniques:

1. Fibonacci Retracements. These are horizontal lines on a chart that indicate areas of support and resistance.
2. Fibonacci Extensions. These are horizontal lines on a chart that indicate where a strong price wave may reach.
3. Fibonacci Arcs. These are compass-like movements stemming from a high or low that represent areas of support and resistance.
4. Fibonacci Fans. These are diagonal lines created using a high and a low that represent areas of support and resistance.
5. Fibonacci Time Zones. These are vertical lines into the future designed to predict when major price movements will occur.

Fibonacci retracements are the most common form of technical analysis based on the Fibonacci sequence. During a trend, Fibonacci retracements can be used to determine how deep a pullback could be. Impulse waves are the larger waves in the trending direction, while pullbacks are the smaller waves in between. Since they are smaller waves, they will be a percentage of the larger wave. Traders will watch the Fibonacci ratios between 23.6% and 78.6% during these times. If the price stalls near one of the Fibonacci levels and then starts to move back in the trending direction, a trader may take a trade in the trending direction.

Fibonacci levels are used as guides, possible areas where a trade could develop. The price should confirm prior to acting on the Fibonacci level. In advance, traders don’t know which level will be significant, so they need to wait and see which level the price respects before taking a trade.

Arcs, fans, extensions and time zones are similar concepts but are applied to charts in different ways. Each one shows potential areas of support or resistance, based on Fibonacci numbers applied to prior price moves. These support or resistance levels can be used to forecast where price may stop falling or rising in the future.

What is the Fibonacci trading strategy?

In the stock market, the Fibonacci trading strategy traces trends in stocks.  When a stock is trending in one direction, some believe that there will be a pullback, or decline in prices.  Fibonacci traders contend a pullback will happen at the Fibonacci retracement levels of 23.6%, 38.2%, 61.8%, or 76.4%. As mentioned below, a pullback is also possible to traders at 50%.

For instance, if GE (NYSE:GE) is selling at $20 and rises to 21, the pullback will be 23, 38, 50, 61, or 76 cents.

Some day trading experts see these Fibonacci numbers as a short-sell strategy. For instance, if GE stock is at $21 and falls to $20.62, some Fibonacci traders may see the 38 cent drop as a good sign to short the stock. For some traders, the Fibonacci retracement is a valid trading strategy to trade stocks.  However, Fibonacci numbers aren’t always the best indicators of a trend.

Golden Ratio

And here is a surprise. When we take any two successive (one after the other) Fibonacci Numbers, their ratio is very close to the Golden Ratio «φ» which is approximately 1.618034…

In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:

A	B		B / A
2	3		1.5
3	5		1.666666666…
5	8		1.6
8	13		1.625
…	…		…
144	233		1.618055556…
233	377		1.618025751…
…	…		…

We don’t have to start with 2 and 3, here I randomly chose 192 and 16 (and got the sequence 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):

A	B		B / A
192	16		0.08333333…
16	208		13
208	224		1.07692308…
224	432		1.92857143…
…	…		…
7408	11984		1.61771058…
11984	19392		1.61815754…
…	…		…

It takes longer to get good values, but it shows that not just the Fibonacci Sequence can do this!

Fibonacci Retracement Pros and Cons

Despite the popularity of Fibonacci retracements, the tools have some conceptual and technical disadvantages that traders should be aware of when using them.

The use of the Fibonacci retracement is subjective. Traders may use this technical indicator in different ways. Those traders who make profits using Fibonacci retracement verify its effectiveness. At the same time, those who lose money say it is unreliable. Others argue that technical analysis is a case of a self-fulfilling prophecy. If traders are all watching and using the same Fibonacci ratios or other technical indicators, the price action may reflect that fact.

The underlying principle of any Fibonacci tool is a numerical anomaly that is not grounded in any logical proof. The ratios, integers, sequences, and formulas derived from the Fibonacci sequence are only the product of a mathematical process. That does not make Fibonacci trading inherently unreliable. However, it can be uncomfortable for traders who want to understand the rationale behind a strategy.

Furthermore, a Fibonacci retracement strategy can only point to possible corrections, reversals, and countertrend bounces. This system struggles to confirm any other indicators and doesn’t provide easily identifiable strong or weak signals.

Что такое расширение Фибоначчи?

Расширение Фибоначчи – это две разнонаправленные трендовые линии, соединенные вместе и связанные с уровнями Фибоначчи, берущими отсчет от 61,8%.

В стандартной интерпретации этого инструмента на множестве торговых платформ, в том числе Metatrader, таких уровней реализовано три: 61.8, 100, 161.8.  Числовой выбор объясняется областью применения инструмента:

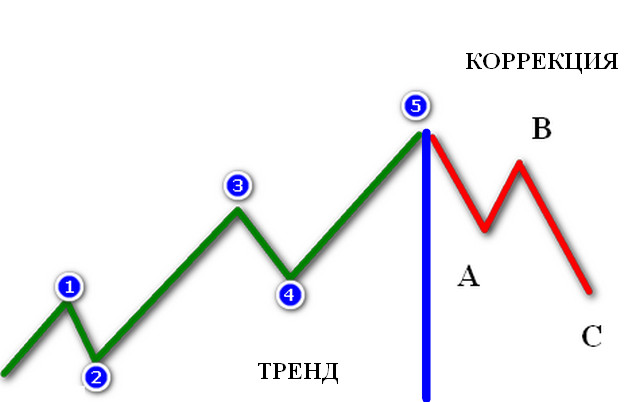
Расширение Фибоначчи представляет собой две волны Эллиотта, как правило, I и II, с целью найти точки коррекции на третьем, самом протяженном по длине, движении тренда.

Применение инструмента предусматривает, что начало волны II выше волны I при восходящем тренде и ниже при нисходящем движении.

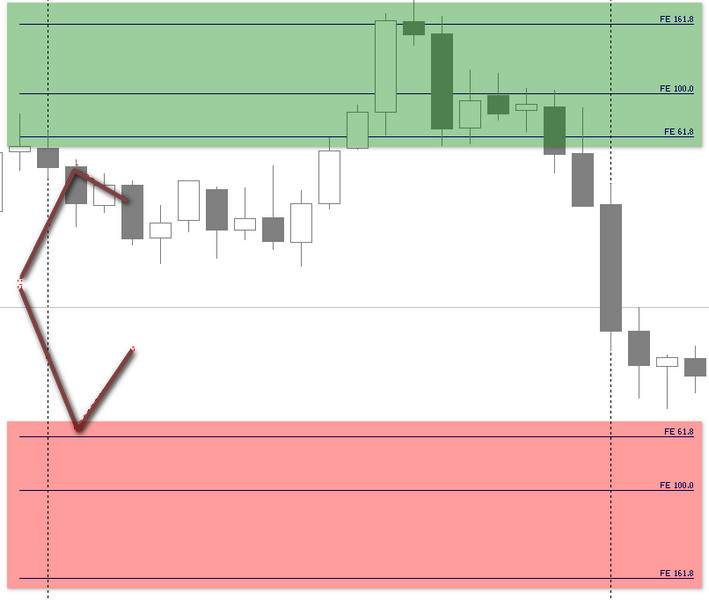Некоторые трейдеры-волновики универсально используют расширение Фибоначчи, располагая его в конце второй волны ниже первой на восходящем тренде, и наоборот — при нисходящем, чтобы подтверждать вершины/впадины коррекционных трех волн ABC.

В обычных волнах Фибоначчи трейдер рассматривает лишь одно трендовое движение, чтобы поймать момент входа на коррекции, представленный, как минимум, тремя уровнями 38,2%, 50% и 61,8%, иногда к ним добавляют 23,8%, «работающий» на сильном, импульсном тренде. Уровни отлично отрабатываются в случае резкого направленного изменения курса валютной пары.

Цифра 61.8% – сигнал для прекращения попыток войти по тренду, указывающий, что он «сломан» такой глубиной коррекции. Поэтому логично, что эта линия выбрана, как первый тейк-профит в расширении Фибоначчи. Работа этого инструмента проходит на уже сложившемся паттерне тренда – это и есть основное отличие между уровнями и расширением:

• Линии Фибоначчи показывают точки входа на развороте по тренду;
• Расширения Фибоначчи прогнозируют точки выхода с прибылью при продолжении тренда.

Спираль Фибоначчи – загадка природы (фото)

Математические науки не знают второй формы, способной сравниться своими свойствами со спиралью, получившей свои оригинальные свойства благодаря положенному в базис структуры Золотое сечение. Напомним, что формула имеет следующий вид: ( a + b )/ a = a / b.

Известный золотой прямоугольник приобрёл своё название именно в честь того, что он обладает как раз таким соотношением сторон — отношение его длинных сторон к меньшим равно 1,168:1.

Рисунок 4. Спираль Фибоначчи проявляется в природе – это загадка последовательности чисел знаменитого ряда Фибоначчи.

Одним из необыкновенных свойств золотого прямоугольника является то, что если от такой фигуры отделить квадрат, с большей стороной равной длине малой стороны прямоугольника, в результате будет получен ещё один золотой прямоугольник, но меньший по площади.

Причём эту операцию можно повторять постоянно, и каждый раз её итогом будет получение золотого прямоугольника ещё меньшего размера. Интересно, что расположение этих прямоугольников будет соответствовать логарифмической спирали, играющей ключевую роль в математических моделях объектов, которые вполне реально обнаружить в природе.

Обычно спиральную структуру наблюдают в закономерности позиций семян подсолнечника, структуре лепестков некоторых видов цветов, в необычной геометрии ракушек.

У подавляющего большинства улиток раковина обладает именно спиралевидной формой. Поскольку эти существа не обладают разумом, они не могут владеть элементарными математическими знаниями, достаточными для создания собственной раковины подобной формы. Многие учёные не могут точно определить причину, по которой эти моллюски сумели выбрать такую необычную форму существования.

Ясно здесь только, что подобное развитие не может считаться случайным стечением обстоятельств, и сама по себе подобная гипотеза будет выглядеть глупо. Это явно осознанное творение.

Спирали легко обнаружить и в теле человека — к такому примеру можно отнести человеческое ухо, внутренне ухо которого так же включает в себя орган, известный как «Улитка», предназначенный для превращения звуковой вибрации в нейронные сигналы. Схожая с костью, эта структура внутри заполнена жидкостью и внешне напоминает улитку, традиционно соответствующую золотым пропорциям.

Спирали также можно найти на ладонях и пальцах человека, элементарно сняв отпечатки.

В животном мире встретить огромное количество спиралевидных форм можно буквально повсюду — закрученные рога и бивни некоторых видов животных, когти и клювы некоторых видов птиц.

Форму спирали принимает и ураган, и лучше всего это можно наблюдать на снимках, сделанных орбитальной космической станцией, глядя, как скручиваются облака циклона.

В волнах, закручивающихся на морской или океанской глади, ясно виден математический график золотого сечения Фибоначчи в природе со значениями 1, 1, 2, 3, 5, 8, 13, 21, 34 и 55. Не стоит так же забывать о водоворотах, или, по крайней мере, о воде, сливающейся в раковине в водосточную трубу.

Рисунок 5. Загадки спирали Фибоначчи в природе до сих пор не разгаданы.

К слову, золотое сечение угадывается даже в форме галактики.

Спираль заслуженно носит звание «Кривой жизни», ведь её причудливая форма имеет место и угадывается во многих областях. Это настоящий символ эволюции, ибо нет такого объекта, чьё развитие не двигалось бы по спирали.

Использование уровней Фибоначчи в трейдинге

Уровни Фибоначчи помогают установить цели движения цены или найти прогнозируемые области поддержки и сопротивления.

К основным уровням, используемым в трейдинге, относятся: 23.6%, 38.2%, 50%, 61.8%, 78.6%, 100%, 161.8%, 261.8%, 423.6%.

Эти соотношения применяются в различных технических индикаторах, использующих коэффициенты Фибоначчи:

• Коррекции Фибоначчи — горизонтальные линии на графике, которые указывают на области поддержки и сопротивления.
• Расширения Фибоначчи — горизонтальные линии на графике, которые указывают, куда может дойти сильная импульсная волна.
• Дуги Фибоначчи — дугообразные линии, построенные относительно локального максимума или минимума, которые представляют собой области поддержки и сопротивления.
• Веера Фибоначчи — диагональные линии, созданные с использованием максимума и минимума, которые представляют собой области поддержки и сопротивления.
• Временные зоны Фибоначчи — вертикальные линии, отложенные в будущее, предназначенные для предсказания того, когда произойдут основные движения цены.

Коррекции Фибоначчи являются наиболее распространенными формами технического анализа, основанными на последовательности Фибоначчи. Во время тренда можно использовать коррекции, чтобы определить, насколько глубоким может быть откат. Импульсные волны — более крупные волны по направлению тренда, в то время как откаты — это более мелкие волны в противоположную от импульсных волн сторону. Так как они являются меньшими волнами, они будут составлять процент от большей волны.

Если цена останавливается около одного из уровней Фибоначчи, а затем начинает двигаться назад в направлении тренда, у трейдера появится возможность совершить сделку по направлению основного тренда. Трейдеры заранее не знают, какой уровень будет разворотным, поэтому необходимо дождаться уровня, на котором остановится и развернется цена, прежде чем заключать сделку.

Дуги, веера, расширения и временные зоны показывает потенциальные области поддержки или сопротивления, основанные на числах Фибоначчи, относительно предыдущих движений цены. Эти уровни поддержки или сопротивления можно использовать для прогнозирования целей, где цена может развернуться в обратную сторону.

Расширения Фибоначчи можно использовать на любом рынке и на любом таймфрейме. Поскольку уровни расширения могут быть нарисованы на разных таймфреймах, необходимо искать области, где несколько уровней из разных волн сходятся на одной цене

Этот уровень может быть очень важной областью, в которой произойдет разворот цены

Свойства

• Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, то есть (Fm,Fn)=F(m,n){\displaystyle (F_{m},F_{n})=F_{(m,n)}}. Следствия:
  • Fm{\displaystyle F_{m}} делится на Fn{\displaystyle F_{n}} тогда и только тогда, когда m{\displaystyle m} делится на n{\displaystyle n} (за исключением n=2{\displaystyle n=2}). В частности, Fm{\displaystyle F_{m}} делится на F3=2{\displaystyle F_{3}=2} (то есть является чётным) только для m=3k{\displaystyle m=3k}; Fm{\displaystyle F_{m}} делится на F4=3{\displaystyle F_{4}=3} только для m=4k{\displaystyle m=4k}; Fm{\displaystyle F_{m}} делится на F5=5{\displaystyle F_{5}=5} только для m=5k{\displaystyle m=5k} и т. д.
  • Fm{\displaystyle F_{m}} может быть простым только для простых m{\displaystyle m} (с единственным исключением m=4{\displaystyle m=4}). Например, число F13=233{\displaystyle F_{13}=233} простое, и его индекс 13 также прост. Обратное не верно, наименьший контрпример — F19=4181=37⋅113{\displaystyle F_{19}=4181=37\cdot 113}. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.

• Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен x2−x−1{\displaystyle x^{2}-x-1} имеет корни φ{\displaystyle \varphi } и −1φ{\displaystyle -{\frac {1}{\varphi }}}.
• Отношения Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}} являются подходящими дробями золотого сечения ϕ{\displaystyle \phi } и, в частности, limn→∞Fn+1Fn=φ.{\displaystyle \lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\varphi .}
• Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы

  Fn+1=∑k=⌊n2⌋(n−kk){\displaystyle F_{n+1}=\sum _{k=0}^{\lfloor n/2\rfloor }{n-k \choose k}}.

• В 1964 году Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12:

  F=2={\displaystyle F_{0}=0^{2}=0}, F1=12=1{\displaystyle F_{1}=1^{2}=1}, F2=12=1{\displaystyle F_{2}=1^{2}=1}, F12=122=144{\displaystyle F_{12}=12^{2}=144}.

• Производящей функцией последовательности чисел Фибоначчи является:

  x+x2+2×3+3×4+5×5+⋯=∑n=∞Fnxn=x1−x−x2{\displaystyle x+x^{2}+2x^{3}+3x^{4}+5x^{5}+\dots =\sum _{n=0}^{\infty }F_{n}x^{n}={\frac {x}{1-x-x^{2}}}}

• Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена

  z(x,y)=2xy4+x2y3−2x3y2−y5−x4y+2y,{\displaystyle z(x,y)=2xy^{4}+x^{2}y^{3}-2x^{3}y^{2}-y^{5}-x^{4}y+2y,}

на множестве неотрицательных целых чисел x и y.

Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.

• Период чисел Фибоначчи по модулю натурального числа n называется периодом Пизано и обозначается π(n). Периоды Пизано π(n) образуют последовательность:

  1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS)

  В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.

• Натуральное число N является числом Фибоначчи тогда и только тогда, когда 5N2+4{\displaystyle 5N^{2}+4} или 5N2−4{\displaystyle 5N^{2}-4} является квадратом.
• Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.
• Число Фибоначчи Fn+2=Fn+1+Fn{\displaystyle F_{n+2}=F_{n+1}+F_{n}} равно количеству кортежей длины n из нулей и единиц, в которых нет двух соседних единиц. При этом Fn+1{\displaystyle F_{n+1}} равно количеству таких кортежей, начинающихся с нуля, а Fn{\displaystyle F_{n}} — начинающихся с единицы.
• Произведение любых n{\displaystyle n} подряд идущих чисел Фибоначчи делится на произведение первых n{\displaystyle n} чисел Фибоначчи.
• Число 0,112358132134… (после запятой записаны подряд идущие числа Фибоначчи) является иррациональным.[источник не указан 1624 дня]

Что думают о последовательности специалисты

Кто-то скажет, что эти числа уже знакомы, потому что они используются в программах технического анализа, для определения величины коррекции и расширения. Кроме того эти же ряды играют важную роль в волновой теории Элиота. Они являются его числовой основой.

Наш эксперт Николай Проверенный портфельный менеджер инвестиционной компании Восток.

• – Николай, как вы думаете, случайно ли появление чисел Фибоначчи и его производных на графиках различных инструментов? И можно ли сказать: «Ряд Фибоначчи практическое применение» имеет место?
• – К мистике отношусь плохо. А на графиках биржи тем более. У всего есть свои причины. Джо Ди Наполи в книге «Уровни Фибоначчи» красиво рассказывал, где появляется золотое сечение, что не стал удивляться тому, что оно появилось на графиках котировок биржи. А зря! Во многих примерах, которые он привел, часто появляется число Пи. Но его почему-то нет в ценовых соотношениях.
• – То есть вы не верите в действенность волнового принципа Элиота?
• – Да нет же, не в этом дело. Волновой принцип – это одно. Численное соотношение – это другое. А причины их появления на ценовых графиках – третье
• – Каковы на ваш взгляд причины появления золотого сечения на биржевых графиках?
• – Правильный ответ на этот вопрос может быть в силах заслужить Нобелевскую премию по экономике. Пока мы можем догадываться об истинных причинах. Они явно не в гармонии природы. Моделей биржевого ценообразования много. Они не объясняют обозначенный феномен. Но не понимание природы явления не должно отрицать явление как таковое.
• – А если когда – либо этот закон будет открыт, то сможет ли это разрушить биржевой процесс?
• – Как показывает та же теория волн закон изменения биржевых цен – это чистая психология. Мне кажется, знание данного закона ничего не изменит и не сможет разрушить биржу.

Материал предоставлен блогом веб-мастера Максима.

Совпадения основ принципов математики в самых разных теориях кажется невероятным. Может быть это фантастика или подгонка под конечный результат. Поживем – увидим. Многое из того, что раньше считалось необычным или было не возможно: освоение космоса, например, стало привычным и никого не удивляет. Также и волновая теория, может быть непонятная, со временем станет доступней и понятней. То, что раньше было не нужным, в руках аналитика с опытом станет мощным инструментом прогнозирования дальнейшего поведения рынка форекс.

Задачи Фибоначчи

Оставаясь верным математическим турнирам, основную роль в своих книгах Фибоначчи отводит задачам, их решениям и комментариям. Задачи на турниры предлагал как сам Фибоначчи, так и его соперник, придворный философ Фридриха II Иоган Палермский. Задачи Фибоначчи, как и их аналоги, продолжали использовать в различных математических учебниках несколько столетий. Их можно встретить в «Сумме арифметики» Пачиоли (1494), в «Приятных и занимательных задачах» Баше де Мизириака (1612), в «Арифметике» Магницкого (1703), в «Алгебре» Эйлера (1768).

Задача о размножении кроликов

Основная статья: Числа Фибоначчи

В место, огороженное со всех сторон стеной, поместили пару кроликов, природа которых такова, что любая пара кроликов производит на свет другую пару каждый месяц, начиная со второго месяца своего существования. Сколько пар кроликов будет через год? (Ответ: 233 пары). Для поиска ответа используется рекуррентная числовая последовательность 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, … (по ней составлена последовательность A000045 в OEIS; отличие в том, что вторая последовательность начинается с нуля и единицы, а не с единицы и двойки), в которой каждое последующее число равно сумме двух предыдущих; ответом, в соответствии с условиями задачи, является тринадцатый член (завершение каждого месяца — это перескок к следующему члену последовательности; текущий член последовательности перед началом опыта — это первый; всего месяцев двенадцать). В честь учёного она носит название чисел Фибоначчи. Числа Фибоначчи нашли своё применение во многих областях математики. Одним из важных свойств последовательности является тот факт, что предел отношения an+1{\displaystyle a_{n+1}} к an{\displaystyle a_{n}} равен золотому сечению. Наглядно формирование последовательности можно показать следующим образом:

1: 1 + 1 = 2
2:     1 + 2 = 3
3:         2 + 3 = 5
4:             3 + 5 = 8
5:                 5 + 8 = 13
6:                     8 + 13 = 21
7:                         13 + 21 = 34
8:                              21 + 34 = 55
9:                                   34 + 55 = 89
...                                           и т. д.

Задачи о гирях

Задача о выборе наилучшей системы гирь для взвешивания на рычажных весах впервые была сформулирована именно Фибоначчи. Леонардо Пизанский предлагает два варианта задачи:

• Простой вариант: требуется найти пять гирь, с помощью которых можно найти все веса меньше 30, при этом гири можно класть только на одну чашу весов (Ответ: 1, 2, 4, 8, 16). Решение строится в двоичной системе счисления.
• Сложный вариант: требуется найти наименьшее число гирь, с помощью которого можно взвесить все веса меньше заданного (Ответ: 1, 3, 9, 27, 81,…). Решение строится в системе счисления по основанию три и в общем случае представляет собой последовательность A000244 в OEIS.

Задачи по теории чисел

Кроме задачи о кроликах, Фибоначчи предлагал ряд других задач по теории чисел:

• Найти число, которое делится на 7 и даёт в остатке единицу при делении на 2, 3, 4, 5 и 6; (Ответ: 301)
• Найти число, произведение которого с семёркой даёт остатки 1, 2, 3, 4, 5 при делении на 2, 3, 4, 5, 6, соответственно;
• Найти квадратное число (то есть число, равное квадрату целого числа), которое при увеличении или уменьшении на 5 давало бы квадратное число.

Некоторые другие задачи

• Найти число, 19/20 которого равно квадрату самого числа. (Ответ: 19/20).
• Сплав из 30 весовых частей состоит из трёх металлов: первый металл достоинством по три монеты на одну часть, второй металл по две монеты на одну часть, а у третьего металла каждые две части стоят по одной монете; стоимость всего сплава 30 монет. Сколько частей каждого металла содержит сплав? (Ответ: 3 части первого металла, 5 частей второго металла, 22 части третьего). В таких терминах Фибоначчи переформулировал известную задачу о птицах, в которой были использованы те же самые числа (30 птиц трёх разных видов стоят 30 монет, по заданным ценам найти количество птиц каждого вида).
• «Шуточная задача о семи старухах», которые шли в Рим, и у каждой было по семь мулов, на каждом из которых по семь мешков, в каждом из которых по семь хлебов, в каждом из которых по семь ножей, каждый из которых в семи ножнах. Нужно найти общее число предметов. Эта задача обошла много стран, первое известное упоминание о ней было ещё в Древнем Египте в папирусе Ахмеса. (Ответ: 137 256).

Some Interesting Things

Here is the Fibonacci sequence again:

n =	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	…
xn =	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	…

There is an interesting pattern:

• Look at the number x₃ = 2. Every 3rd number is a multiple of 2 (2, 8, 34, 144, 610, …)
• Look at the number x₄ = 3. Every 4th number is a multiple of 3 (3, 21, 144, …)
• Look at the number x₅ = 5. Every 5th number is a multiple of 5 (5, 55, 610, …)

And so on (every nth number is a multiple of x_n).

1/89 = 0.011235955056179775…

Notice the first few digits (0,1,1,2,3,5) are the Fibonacci sequence?

In a way they all are, except multiple digit numbers (13, 21, etc) overlap, like this:

0.0
0.01
0.001
0.0002
0.00003
0.000005
0.0000008
0.00000013
0.000000021
… etc …
0.011235955056179775…  =  1/89

Расширение на вещественные и комплексные числа

Существует много возможных обобщений, которые расширяют числа Фибоначчи на вещественные числа (а иногда и на комплексные числа). Они используют золотое сечение φ и базируются на формуле Бине

Fn=φn−(−φ)−n5.{\displaystyle F_{n}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{\sqrt {5}}}.}

Аналитическая функция

Fe⁡(x)=φx−φ−x5{\displaystyle \operatorname {Fe} (x)={\frac {\varphi ^{x}-\varphi ^{-x}}{\sqrt {5}}}}

имеет свойство, что Fe⁡(n)=Fn{\displaystyle \operatorname {Fe} (n)=F_{n}} для чётных целых чисел n. Аналогично, для аналитической функции

Fo⁡(x)=φx+φ−x5{\displaystyle \operatorname {Fo} (x)={\frac {\varphi ^{x}+\varphi ^{-x}}{\sqrt {5}}}}

выполняется Fo⁡(n)=Fn{\displaystyle \operatorname {Fo} (n)=F_{n}} для всех нечётных целых чисел n.

Собирая всё вместе, получим аналитическую функцию

Fib⁡(x)=φx−cos⁡(xπ)φ−x5,{\displaystyle \operatorname {Fib} (x)={\frac {\varphi ^{x}-\cos(x\pi )\varphi ^{-x}}{\sqrt {5}}},}

для которой выполняется Fib⁡(n)=Fn{\displaystyle \operatorname {Fib} (n)=F_{n}} для всех целых чисел n.

Поскольку Fib⁡(z+2)=Fib⁡(z+1)+Fib⁡(z){\displaystyle \operatorname {Fib} (z+2)=\operatorname {Fib} (z+1)+\operatorname {Fib} (z)} для всех комплексных чисел z, эта функция даёт также расширение последовательности Фибоначчи для всей комплексной плоскости. Таким образом, мы можем вычислить обобщённую функцию Фибоначчи для комплексной переменной, например,

Fib⁡(3+4i)≈−5248,5−14195,9i.{\displaystyle \operatorname {Fib} (3+4i)\approx -5248{,}5-14195{,}9i.}

Научная деятельность

Книга абака

Значительную часть усвоенных им знаний он изложил в своей «Книге абака» (Liber abaci, 1202 год; до наших дней сохранилась только дополненная рукопись 1228 года). Эта книга состоит из 15 глав и содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной. Первые пять глав книги посвящены арифметике целых чисел на основе десятичной нумерации. В VI и VII главе Леонардо излагает действия над обыкновенными дробями. В VIII—X главах изложены приёмы решения задач коммерческой арифметики, основанные на пропорциях. В XI главе рассмотрены задачи на смешение. В XII главе приводятся задачи на суммирование рядов — арифметической и геометрической прогрессий, ряда квадратов и, впервые в истории математики, возвратного ряда, приводящего к последовательности так называемых чисел Фибоначчи. В XIII главе излагается правило двух ложных положений и ряд других задач, приводимых к линейным уравнениям. В XIV главе Леонардо на числовых примерах разъясняет способы приближённого извлечения квадратного и кубического корней. Наконец, в XV главе собран ряд задач на применение теоремы Пифагора и большое число примеров на квадратные уравнения. Леонардо впервые в Европе использовал отрицательные числа, которые рассматривал как долг. Книга посвящена Майклу Скоту.

Другая книга Фибоначчи, «Практика геометрии» (Practica geometriae, 1220 год), состоит из семи частей и содержит разнообразные теоремы с доказательствами, относящиеся к измерительным методам. Наряду с классическими результатами Фибоначчи приводит свои собственные — например, первое доказательство того, что три медианы треугольника пересекаются в одной точке (Архимеду этот факт был известен, но если его доказательство и существовало, до нас оно не дошло). Среди землемерных приёмов, которым посвящён последний раздел книги, — использование определённым образом размеченного квадрата для определения расстояний и высот. Для определения числа π{\displaystyle \pi } Фибоначчи использует периметры вписанного и описанного 96-угольника, что приводит его к значению 3,1418{\displaystyle 3,1418}. Книга была посвящена Доминикусу Хиспанусу. В 1915 году Р. С. Арчибальд занимался восстановлением утерянной работы Евклида о делении фигур, базируясь на «Практике геометрии» Фибоначчи и французском переводе арабской версии.

В трактате «Цветок» (Flos, 1225 год) Фибоначчи исследовал кубическое уравнение x3+2×2+10x=20{\displaystyle x^{3}+2x^{2}+10x=20}, предложенное ему Иоанном Палермским на математическом состязании при дворе императора Фридриха II. Сам Иоанн Палермский почти наверняка заимствовал это уравнение из трактата Омара Хайяма «О доказательствах задач алгебры», где оно приводится как пример одного из видов в классификации кубических уравнений. Леонардо Пизанский исследовал это уравнение, показав, что его корень не может быть рациональным или же иметь вид одной из квадратичных иррациональностей, встречающихся в X книге Начал Евклида, а затем нашёл приближённое значение корня в шестидесятеричных дробях, равное 1;22,07,42,33,04,40, не указывая, однако, способа своего решения.

«Книга квадратов» (Liber quadratorum, 1225 год) содержит ряд задач на решение неопределённых квадратных уравнений. Фибоначчи работал над поиском чисел, которые, будучи добавленными к квадратному числу, вновь дадут квадратное число. Он отметил, что числа x2+y2{\displaystyle x^{2}+y^{2}} и x2−y2{\displaystyle x^{2}-y^{2}} не могут быть квадратными одновременно, а также использовал для поиска квадратных чисел формулу x2+(2x+1)=(x+1)2{\displaystyle x^{2}+(2x+1)=(x+1)^{2}}. В одной из задач книги, также первоначально предложенной Иоанном Палермским, требовалось найти рациональное квадратное число, которое, будучи увеличено или уменьшено на 5, вновь даёт рациональные квадратные числа.

Среди не дошедших до нас произведений Фибоначчи трактат Di minor guisa по коммерческой арифметике, а также комментарии к книге X «Начал» Евклида.

Как появились числа и их производные

Решая прикладную задачу, Леонардо наткнулся на любопытный ряд чисел Фибоначчи, вначале которого находятся две единицы.

Каждый последующий член – это сумма двух предыдущих. Самое любопытное, что числовой ряд Фибоначчи – примечательная последовательность тем, что если любой член поделить на предыдущий, то получится число, которое близко к 0,618. Этому числу дали имя «Золотое сечение».

Оказалось, что это число было известно человечеству очень давно. Например, в древнем Египте строили пирамиды с его использованием, а древние греки возводили по нему свои храмы. Леонардо да Винчи показал, как строение тела человека подчиняется этом числу.

Природа применяет числа из ряда Фибоначчи в своих наиболее сокровенных и продвинутых областях. От атомных структур и других мелких форм, как молекулы ДНК и микрокапилляры мозга до огромных, как планетарные орбиты и структуры галактик. Ряд примеров настолько велик, что следует утверждать, что в природе действительно присутствует некий основной закон пропорций.

Поэтому не удивительно, что ряд Фибоначчи и золотое сечение пробралось и на биржевые графики. И не одно число 0,618, но и его производные.

Если число золотого сечения возвести в первую, вторую, третью и четвертую степень и вычесть результат из единицы, то получиться новый ряд, который носит название «коэффициенты коррекции Фибоначчи». Осталось только добавить отметку пять десятых – это пятидесятипроцентная коррекция Чарльза Доу.

Однако, это не все, что можно сделать с золотым сечением. Если единицу разделить на 0,618 то получается 1,618, если возведем в квадрат, то у нас получится 2,618, если возведем в куб, то получим число 4,236. Это коэффициенты расширения Фибоначчи. Тут не хватает только числа 3,236, которое было предложено Джоном Мёрфи.

Последовательность Фибоначчи (числа Фибоначчи)

Фибоначчи перенял большую часть своей работы от предшественников, он не только систематизировал, но и обогатил ее. Его имя до сих пор ассоциируется с одним открытием. Отправной точкой для этого была изначально странно выглядящая проблема:

1. Одна пара кроликов рождает новую пару каждый месяц
2. Каждая новая пара создает новую пару каждый месяц со второго месяца
3. За это время не было ни одной смерти

В первом месяце есть только одна пара, во втором — уже две пары. В третьем месяце добавляется новая пара из первой пары, а в четвертом — новая пара из первой и второй пары, так что всего их пять. Это приводит к следующей последовательности: 1; 2; 3; 5; …

Если поместить 1 перед первым элементом в качестве дополнительного элемента, то получится так называемая последовательность Фибоначчи (числа Фибоначчи):

Каждый элемент является суммой двух предыдущих. Это первая известная рекурсивно определенная последовательность. Фибоначчи изучил эту последовательность и обнаружил много замечательных свойств, таких как:

Сумма первых n членов равна числу Фибоначчи — 1(например: 1 + 1 + 2 + 3 + 5 + 8 = 21 — 1)Сумма квадратов двух соседних чисел Фибоначчи снова приводит к числу Фибоначчи.(например: 32 + 52 = 34).

Только намного позже оказалось, что эта последовательность играет важную роль в других математических задачах, таких как золотое сечение и треугольник Паскаля, и что, например, разветвления деревьев, как правило, следуют этому закону.

Chapter 2: Key Fibonacci Ratios

Fibonacci discovered every number in the sequence is approximately 61.8% of the next number in the sequence.

55 / 89 = 0.6179775280898876 = 61.8%

233 / 377 = 0.6180371352785146 = 61.8%

144 / 233 = 0.6180257510729614 = 61.8%

This is not the only correlation. Fibonacci also uncovered that every number in the sequence is approximately 38.2% of the Fibonacci number two steps ahead.

(13, 21, 34)

13 / 34 = 0.3823529411764706 = 38.2%

(21, 34, 55)

21 / 55 = 0.3818181818181818 = 38.2%

(55, 89, 144)

55 / 144 = 0.3819444444444444 = 38.2%

(144, 233, 377)

Develop Your Trading 6th Sense

No more panic, no more doubts. make the right decisions because you’ve seen it with your trading simulator, TradingSim.

Learn About TradingSim

144 / 377 = 0.3819628647214854 = 38.2%

Also, we have another ratio! Every number in the Fibonacci sequence is 23.6% of the number after the next two numbers in the sequence:

(55, 89, 144, 233)

55 / 233 = 0.2360515021459227 = 23.6%