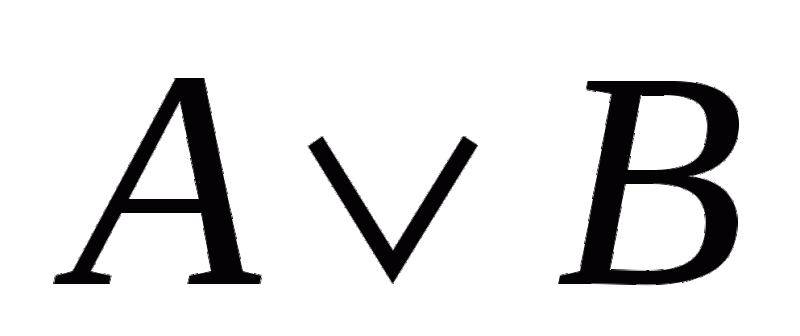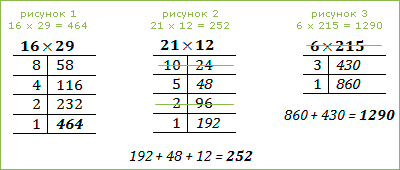Римские цифры: от 1 до 50. как перевести арабское число в римское и обратно

Обобщения чисел

Кватернионы, представляющие собой разновидность гиперкомплексных чисел. Множество кватернионов обозначается H{\displaystyle \mathbb {H} }. Кватернионы в отличие от комплексных чисел не коммутативны относительно умножения.

В свою очередь октавы O{\displaystyle \mathbb {O} }, являющиеся расширением кватернионов, уже теряют свойство ассоциативности.

В отличие от октав, седенионы S{\displaystyle \mathbb {S} } не обладают свойством альтернативности, но сохраняют свойство степенной ассоциативности.

Для этих множеств обобщённых чисел справедливо следующее выражение: C⊂H⊂O⊂S{\displaystyle \mathbb {C} \subset \mathbb {H} \subset \mathbb {O} \subset \mathbb {S} }

p-адические числа Qp{\displaystyle \mathbb {Q} _{p}} можно рассматривать как элементы поля, являющегося пополнением поля рациональных чисел Q{\displaystyle \mathbb {Q} } при помощи т. н. , аналогично тому, как поле действительных чисел R{\displaystyle \mathbb {R} } определяется как его пополнение при помощи обычной абсолютной величины.

Аде́ли определяются как бесконечные последовательности {a_∞,a₂,a₃,…a_p…}, где a_∞ — любое действительное число, а a_p — p-адическое, причём все a_p, кроме, может быть, конечного их числа, являются целыми p-адическими. Складываются и умножаются адели покомпонентно и образуют кольцо. Поле рациональных чисел вкладывается в это кольцо обычным образом r→{r, r,…r,…}. Обратимые элементы этого кольца образуют группу и называются иде́лями.

Практически важным обобщением числовой системы является интервальная арифметика.

Из истории математики

Десятеричная система исчисления прижилась у людей потому, что именно пальцы рук, которых, как известно 10, использовались первоначально для подсчетов. Но у цивилизаций майя и чукчей раньше была в ходу двадцатеричная система исчисления, поскольку они использовали в счете пальцы не только рук, но и ног.

Автором знака «=» является математик XVI в. Роберт Рекорд, которому просто надоело писать в каждом уравнении слово «равно».

Некоторые считают, Альфред Нобель застал свою жену за изменой с математиком, поэтому в перечне дисциплин одноименной премии математика отсутствует. Удивительный факт, но в действительности Нобель даже не был ни разу женат. Что касается причин, то доподлинные так и остались неизвестными, а среди возможных предположений выдвигаются следующие:

• К тому моменту уже существовала одна премия в области математики, утвержденная шведским королем.
• Нобель считал, математика – исключительно теоретическая наука, поэтому с ее помощью невозможно делать важные для человечества изобретения.

Все современные математические знания с трудом можно уместить в 100 000 учебников, тогда как в 1900 г. для этого понадобилось бы не более 80 книг.

Представление чисел в памяти компьютера

подробнее см. Прямой код, Дополнительный код (представление числа), Число с плавающей запятой

Для представления натурального числа в памяти компьютера, оно обычно переводится в двоичную систему счисления. Для представления отрицательных чисел часто используется дополнительный код числа, который получается путём прибавления единицы к инвертированному представлению модуля данного отрицательного числа в двоичной системе счисления.

Представление чисел в памяти компьютера имеет ограничения, связанные с ограниченностью объёма памяти, выделяемого под числа. Даже натуральные числа представляют собой математическую идеализацию, ряд натуральных чисел бесконечен. На объём же памяти ЭВМ накладываются физические ограничения. В связи с этим в ЭВМ мы имеем дело не с числами в математическом смысле, а с некоторыми их представлениями, или приближениями. Для представления чисел отводится некоторое определённое число ячеек (обычно двоичных, бит — от BInary digiT) памяти. В случае, если в результате выполнения операции полученное число должно занять больше разрядов, чем отводится в ЭВМ, результат вычислений становится неверным — происходит так называемое арифметическое переполнение. Действительные числа обычно представляются в виде чисел с плавающей запятой. При этом лишь некоторые из действительных чисел могут быть представлены в памяти компьютера точным значением, в то время как остальные числа представляются приближёнными значениями. В наиболее распространённом формате число с плавающей запятой представляется в виде последовательности битов, часть из которых кодирует собой мантиссу числа, другая часть — показатель степени, и ещё один бит используется для указания знака числа.

Основные числовые множества

Натуральные числа (N{\displaystyle \mathbb {N} }) — числа, получаемые при естественном счёте: N={1,2,3,…}.{\displaystyle \mathbb {N} =\left\{1,2,3,…\right\}.} Иногда к множеству натуральных чисел также относят ноль, то есть N={0,1,2,3,…}{\displaystyle \mathbb {N} =\left\{0,1,2,3,…\right\}}. Натуральные числа замкнуты относительно сложения и умножения (но не вычитания или деления). Сложение и умножение натуральных чисел коммутативны и ассоциативны, а умножение натуральных чисел дистрибутивно относительно сложения и вычитания.

Целые числа (Z{\displaystyle \mathbb {Z} }) — числа, получаемые объединением натуральных чисел со множеством чисел противоположных натуральным и нулём, обозначаются Z={…−2,−1,0,1,2,…}{\displaystyle \mathbb {Z} =\left\{…-2,-1,0,1,2,…\right\}}. Любое целое число можно представить как разность двух натуральных. Целые числа замкнуты относительно сложения, вычитания и умножения (но не деления); в общей алгебре такая алгебраическая структура называется кольцом.

Рациональные числа (Q{\displaystyle \mathbb {Q} }) — числа, представимые в виде дроби m/n (n ≠ 0), где m — целое число, а n — натуральное число. Рациональные числа замкнуты уже относительно всех четырёх арифметических действий: сложения, вычитания, умножения и деления (кроме деления на ноль); в общей алгебре такая алгебраическая структура называется полем. Для обозначения рациональных чисел используется знак Q{\displaystyle \mathbb {Q} } (от англ. quotient).

Действительные (вещественные) числа (R{\displaystyle \mathbb {R} }) — числа, представляющие собой расширение множества рациональных чисел, замкнутое относительно некоторых (важных для математического анализа) операций предельного перехода. Множество вещественных чисел обозначается R{\displaystyle \mathbb {R} }. Его можно рассматривать как пополнение поля рациональных чисел Q{\displaystyle \mathbb {Q} } при помощи нормы, являющейся обычной абсолютной величиной. Кроме рациональных чисел, R{\displaystyle \mathbb {R} } включает множество иррациональных чисел I{\displaystyle \mathbb {I} }, не представимых в виде отношения целых.

Комплексные числа (C{\displaystyle \mathbb {C} }) — числа, являющиеся расширением множества действительных чисел. Они могут быть записаны в виде z=x+iy{\displaystyle z=x+iy}, где i — т. н. мнимая единица, для которой выполняется равенство i2=−1{\displaystyle i^{2}=-1}. Комплексные числа используются при решении задач электротехники, гидродинамики, картографии, квантовой механики, теории колебаний, теории хаоса, теории упругости и многих других. Комплексные числа подразделяются на алгебраические и трансцендентные. При этом каждое действительное трансцендентное является иррациональным, а каждое рациональное число — действительным алгебраическим. Более общими (но всё ещё счётными) классами чисел, чем алгебраические, являются периоды, вычислимые и арифметические числа (где каждый последующий класс шире, чем предыдущий).

Для перечисленных множеств чисел справедливо следующее выражение: N⊂Z⊂Q⊂R⊂C.{\displaystyle \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C} .}

Число в философии

Философское понимание числа заложили пифагорейцы. Аристотель свидетельствует, что пифагорейцы считали числа «причиной и началом» вещей, а отношения чисел — основой всех отношений в мире. Числа придают миру упорядоченность и делают его космосом. Такое отношение к числу было принято Платоном, а позже неоплатониками. Платон при помощи чисел различает подлинное бытие (то, что существует и мыслится само по себе), и неподлинное бытие, (то, что существует лишь благодаря другому и познаётся только в отношении). Срединное положение между ними занимает число. Оно придаёт меру и определённость вещам и делает их причастными бытию. Благодаря числу вещи могут быть подвергнуты пересчёту и поэтому они могут быть мыслимы, а не только ощущаемы. Неоплатоники, особенно Ямвлих и Прокл, почитали числа столь высоко, что даже не считали их сущими — устроение мира исходит от числа, хотя и не непосредственно. Числа сверхсущны, пребывают выше Ума, и недоступны знанию. Неоплатоники различают божественные числа (прямую эманацию Единого) и математические числа (составленные из единиц). Последние являются несовершенными подобиями первых. Аристотель, наоборот, приводит целый ряд аргументов, показывающих, что утверждение о самостоятельном существовании чисел приводит к нелепостям. Арифметика выделяет в этих реально сущих вещах только один аспект и рассматривает их с точки зрения их количества. Числа и их свойства являются результатом такого рассмотрения. Кант считал, что явление познано тогда, когда оно сконструировано в соответствии с априорными понятиями — формальными условиями опыта. Число — одно из таких условий. Число задаёт конкретный принцип или схему конструирования. Любой объект является исчислимым и измеряемым, потому что он сконструирован по схеме числа (или величины). Поэтому всякое явление может рассматриваться математикой. Разум воспринимает природу подчинённой числовым закономерностям именно потому, что сам строит её в соответствии с числовыми закономерностями. Так объясняется возможность применения математики в изучении природы. Математические определения, разработанные в XIX веке, были серьёзно пересмотрены в начале XX века. Это было вызвано не столько математическими, сколько философскими проблемами. Определения, которые были даны Пеано, Дедекиндом или Кантором, и которые используются в математике и в настоящее время, нужно было обосновать с помощью фундаментальных принципов, коренящихся в самой природе знания. Различают три таких философско-математических подхода: логицизм, интуиционизм и формализм. Философскую базу логицизма разработал Рассел. Он полагал, что истинность математических аксиом неочевидна. Истинность обнаруживается сведением к наиболее простым фактам. Отражением таких фактов Рассел считал аксиомы логики, которые он положил в основу определения числа. Важнейшим понятием у него является понятие класса. Натуральное число η есть класс всех классов, содержащих η элементов. Дробь — это уже не класс, а отношение классов. Интуицист Брауэр имел противоположную точку зрения: логику он считал лишь абстракцией от математики, рассматривал натуральный ряд чисел как базовую интуицию, лежащую в основании всякой мыслительной деятельности. Гильберт, главный представитель формальной школы, видел обоснование математики в построении непротиворечивой аксиоматической базы, в пределах которой можно бы было формально обосновать любое математическое понятие. В разработанной им аксиоматической теории действительных чисел представление о числе лишается всякой глубины и сводится лишь к графическому символу, подставляемому по определённым правилам в формулы теории.

О цифрах и числах

Если сложить все числа от 1 до 100, их сумма будет равна 5050.

2 и 5 – единственные простые числа (то есть те, которые делятся только на сами себя и на 1) которые заканчиваются на 2 и 5.

Зеркальные числа, то есть те, что читаются в обеих направлениях одинаково, имеют название палиндромы (к примеру, 12321 или 4567654).

Самое большое число в мире, которое имеет название и встречается в словарях, пишется как 1 и 600 нулей (или 10600) и называется центиллион.

Самое маленькое число пока существует без названия и является десятичной дробью, у которой сразу после запятой и перед 1 следует 100 миллионов триллионов триллионов триллионов нулей. Ученые используют его только для вычисления вероятности развития новой Вселенной из любого атома.

Самым мистическим считается 666 – как говорится в одном из стихов книги Откровения, знак антихриста. С ним связаны различные удивительные факты не только в математике, но и в повседневной жизни:

• Сумма значений, нарисованных на барабане рулетки в казино составляет 666, поэтому ее часто называют «чертово колесо».
• По негласной традиции кресло в Европарламенте под номером 666 всегда остается пустым.
• В большинстве стран невозможно встретить маршрут поезда или общественного транспорта, номер шоссе, телефонный код или другие объекты с маркировкой 666.
• Психологическое заболевание, связанное с боязнью знака 666 называется – гексакосиойгексеконтагексафобия (Hexakosi-oidekahexaphobia).

Что такое цифра?

Это вопрос, на который мы получаем ответ изначально от родителей, потом от преподавателей в учебных заведениях. Что такое цифра? А из словаря Владимира Даля можно узнать, что цифры — это численные показатели. Именно они представляются символами чисел. Нам известно всего 10 цифр: от нуля до девяти. Из их сочетания получается бесконечность чисел. Какие же существуют цифры?

• Арабские. Такими символами мы пользуемся довольно-таки давно. Они возникли в Европе еще в 10-м веке.
• Римские. Возникли еще за пять веков до нашей эры и находились в обиходе у племен этрусков, проживавших на Апеннинском полуострове.
• Цифры майя. Такие знаки использовались для расчетов в календаре.

Но в современном мире цифра — это не только математический знак, и сегодняшний день существует даже цифровое телевидение, а также существует цифровой формат.

Угадывание чисел

Игры с угадыванием чисел или даты рождения – очень полезное развлечение, отлично развивающее навыки быстрого умственного счёта. Суть заключается в том, что желающий загадывает число. Затем производит по указанию ведущего различные математические действия над ним и говорит полученный результат. Ведущий с помощью нехитрой уловки мгновенно называет загаданное число. Таких задач существует невероятно много. Рассмотрим одну из них. Задание для участника: задумайте число. Умножьте его на три. Поделите пополам (если число не делится нацело на два, прибавьте к нему единицу и поделите пополам). Полученную половину утройте. Скажите, сколько раз содержится 9 в полученном числе.

Чтобы угадать задуманное число, ведущему достаточно умножить количество девяток на два. Если же при делении участнику пришлось добавлять единицу, то количество девяток нужно умножить на два и также прибавить единицу.

Арабские цифры.

Арабские цифры

В V веке в Индии появилась система записи, которую мы знаем как арабские цифры и активно используем сейчас. Это был набор из 9 цифр от 1 до 9. Каждая цифра записывалась так, чтобы ей соответствовало количество углов. Например, в цифре 1 — один угол, в цифре 2 — два угла, в цифре 3 — три. И так до 9. Нуля еще не существовало, он появился позже. Вместо него просто оставляли пустое место.

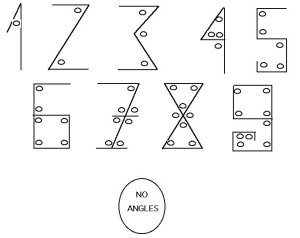
Запись цифры по числу углов

Далее произошло интересное: арабы переняли индийскую систему счисления и начали вовсю применять ее. В те времена мусульманский мир был очень развит, он имел очень тесные связи и с азиатской и европейской культурой и брал от них все самое совершенное и передовое на то время.

Математик Мухаммед Аль-Хорезми в IX веке составил руководство об индийской нумерации. Оно в XII веке попало в Европу и эта система счисления получило очень широкое распространение. Интересно, но именно из-за того, что к нам эти цифры пришли от арабов, мы их называем арабскими, а не индийскими.

Кстати, и само слово «цифра» — арабского происхождения. Арабы перевели индийское «сунья» и получилось «цифр».

Арабская система счисления называется позиционной. Это значит, что значение числа зависит от положения его в записи. То есть в числе 18 цифра 8 обозначает 8 единиц, а в числе 87 та же восьмерка обозначает 8 десятков. Позиционные системы наиболее совершенны. Но они произошли от непозиционных систем (которые, в принципе, существуют и сейчас) в результате развития человечества, его знаний и потребностей.

Интересно то, что современные арабские цифры сильно отличаются от тех, которые используем мы:

Современные арабские цифры

Вот такая история чисел. Сейчас тоже используются разные числа. Некоторые страны, как например, арабские страны и Китай, пользуются своими особенными цифрами. Но, все-таки, наибольшее распространение получили арабские цифры, которые используют и понимают во всем мире.

Вам также может быть интересно:

Иерархия чисел

Ниже представлена иерархия чисел, для множеств которых справедливо выражение N⊂Z⊂Q⊂R⊂C⊂H⊂O⊂S{\displaystyle \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C} \subset \mathbb {H} \subset \mathbb {O} \subset \mathbb {S} }, с примерами:

Что такое цифра?

Цифра — это упорядоченная знаковая система, предназначенная для записи чисел. Цифрами считаются только те символы, которые в отдельности обозначают числа. Например, знак «-» хоть и применяется для того, чтобы записать число, но цифрой он не считается. Цифрами считается ряд от 0 до 9. Само слово «цифра» имеет арабские корни и обозначает «ноль» или «пустое место». Эти символы бывают следующих видов:

Это перечислены самые известные разновидности. В разных языках, например, в древнегреческом, для записи чисел используют буквы. Чаще всего в обиходной речи люди под словом «цифры» подразумевают числа, которыми записываются числовые данные. Следует помнить, что отрицательных, дробных и натуральных цифр не существует.

Привычная нам система исчисления основывается на цифрах арабского происхождения, которые стали известны европейцам в 13-м веке. До этого для записи чисел использовали римские графические символы. Сейчас эту разновидность можно увидеть на циферблате часов, а также в книгах.

Число — это основное математическое понятие. Его используют для:

• количественной характеристики;
• сравнения;
• обозначения нумерации объектов.

Числа записываются цифрами и иногда при помощи символов операций в математике. Они возникли еще в первобытном обществе, когда появилась потребность в счете. Числа бывают:

• натуральные — получаются при естественном счете;
• целые — получаются при помощи объединения натуральных чисел;
• рациональные — имеют вид дроби;
• действительные;
• комплексные.

Два последних вида чисел имеют важное значение для математического анализа и получаются благодаря расширению рациональных (для действительных) и действительных (для комплексных) чисел. Если в древние времена числа были нужны для перечисления, то с научным прогрессом их значение возросло

Если в древние времена числа были нужны для перечисления, то с научным прогрессом их значение возросло.

1. С числами можно проводить различные математические действия. С цифрами такого делать нельзя.
2. Число может быть отрицательным, дробным, в отличие от цифр.
3. Количество цифр всего 10, а чисел — бесконечное множество, т.к. они состоят из цифр.

Кроме различий, с математической точки зрения, существуют и лингвистические отличия. Они рассматривают, в каких случаях можно говорить «цифра», а когда — «число». Если в разговоре упоминаются официальные показатели, то уместно говорить слово «цифра». Это могут быть, например, статистические данные.

Понятие «цифры» широко распространено в нумерологии. Нумерологи используют это понятие как знак, который способен влиять на судьбу человека. Они наделяют его мистическими свойствами. Например, нумерологи уверены в том, что некоторые цифры притягивают удачу.

Число употребляют тогда, когда нужно назвать количество чего-либо, или когда речь идет о календарной дате или дне месяца. В русском языке для употребления этого понятия применяются порядковые числительные.

По сравнению с первобытными и древними обществами, у понятия «цифра» расширилась область употребления. Теперь это — не только в математике. Сейчас люди говорят о цифровом телевидении, цифровом формате. Так же и с числами — теперь они применяются, например, в информатике. Получается, что с развитием общества и науки развиваются и математические понятия. После прочтения всех математических и лингвистических тонкостей читатели знают, чем отличается число от цифры.

Всем людям с раннего детства знакомы цифры, с помощью которых ведется счет предметов. Их всего десять: от 0 до 9. Потому и система исчисления называется десятичной. С помощью них можно записать совершенно любое число.

Тысячелетиями люди применяли свои пальцы для обозначения чисел. Сегодня десятичная система используется повсюду: для измерения времени, при продаже и покупке чего-либо, при различных расчетах. Каждый человек имеет собственные числа, например, в паспорте, на кредитной карте.

Появление чисел

Интуитивное представление о числе, по–видимому, так же старо, как и само человечество, хотя с достоверностью проследить все ранние этапы его развития в принципе невозможно. Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и двух людей или двух и многих людей. То, что первобытные люди сначала знали только “один”, “два” и “много”, подтверждается тем, что в некоторых языках, например в греческом, существуют три грамматические формы: единственного числа, двойственного числа и множественного числа. Позднее человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми. Счет изначально был связан с вполне конкретным набором объектов, и самые первые названия чисел были прилагательными. Например, слово “три” использовалось только в сочетаниях “три дерева” или “три человека”; представление о том, что эти множества имеют между собой нечто общее – понятие троичности – требует высокой степени абстракции. О том, что счет возник раньше появления этого уровня абстракции, свидетельствует тот факт, что слова “один” и “первый”, равно как “два” и “второй”, во многих языках не имеют между собой ничего общего, в то время как лежащие за пределами первобытного счета “один”, “два”, “много”, слова “три” и “третий”, “четыре” и “четвертый” ясно указывают на взаимосвязь между количественными и порядковыми числительными.

Названия чисел, выражающие весьма абстрактные идеи, появились, несомненно, позже, чем первые грубые символы для обозначения числа объектов в некоторой совокупности. В глубокой древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке, выложенных в ряд камешков, причем подразумевалось, что между пересчитываемыми элементами множества и символами числовой записи существует взаимно однозначное соответствие. Но для чтения таких числовых записей названия чисел непосредственно не использовались. Ныне мы с первого взгляда распознаем совокупности из двух, трех и четырех элементов; несколько труднее распознаются на взгляд наборы, состоящие из пяти, шести или семи элементов. А за этой границей установить на глаз их число практически уже невозможно, и нужен анализ либо в форме счета, либо в определенном структурировании элементов. Счет на бирках, по–видимому, был первым приемом, который использовался в подобных случаях: зарубки на бирках располагались определенными группами подобно тому, как при подсчете избирательных бюллетеней их часто группируют пачками по пять или десять штук. Очень широко был распространен счет на пальцах, и вполне возможно, что названия некоторых чисел берут свое начало именно от этого способа подсчета.

Важная особенность счета заключается в связи названий чисел с определенной схемой счета. Например, слово “двадцать три” – не просто термин, означающий вполне определенную (по числу элементов) группу объектов; это термин составной, означающий “два раза по десять и три”. Здесь отчетливо видна роль числа десять как коллективной единицы или основания; и действительно, многие считают десятками, потому что, как отметил еще Аристотель, у нас по десять пальцев на руках и на ногах. По той же причине использовались основания пять или двадцать. На очень ранних стадиях развития истории человечества за основания системы счисления принимались числа 2, 3 или 4; иногда для некоторых измерений или вычислений использовались основания 12 и 60.

Считать человек начал задолго до того, как он научился писать, поэтому не сохранилось никаких письменных документов, свидетельствовавших о тех словах, которыми в древности обозначали числа. Для кочевых племен характерны устные названия чисел, что же касается письменных, то необходимость в них появилась лишь с переходом к оседлому образу жизни, образованием земледельческих сообществ. Возникла и необходимость в системе записи чисел, и именно тогда было заложено основание для развития математики.

Что такое число?

Мы узнали, что такое цифра, но понятие числа все еще неизвестно. Числа — это отвлеченные понятия, которые используются для численной функциональности каких-либо объектов. Они появились еще в обществе первобытных людей. Уже в те времена возникла потребность в счете. Со временем числа преобразовывались и дополнялись. В итоге они оказались первым математическим суждением. Какие же имеются числа?

• Натуральные. Их мы получаем при естественном счислении. Натуральные числа применяются нами ежедневно.
• Целые. Их мы получаем путем объединения натуральных чисел с множеством отрицательных чисел и с нулем. Они ограничены в сложении, вычитании и умножении, но не в делении.
• Рациональные. Они отображаются чаще всего в виде дроби. Для рациональных чисел характерны все четыре арифметические действия: сложение, умножение, вычитание и деление.
• Действительные — это множество рациональных чисел, которые делятся на алгебраические и трансцендентные.
• Комплексные. Они представлены расширением большого количества действительных чисел. Они находятся в обиходе при решении задач гидродинамики, теории упругости, квантовой механики.

Заключение

Из нашей статьи вы узнали о том, как называются цифры, которые мы используем. Теперь вы с легкостью можете ответить на этот вопрос, а также рассказать удивительную историю о том, что их придумали вовсе не арабы, а индусы.

Заслуга арабов заключается лишь в том, что они со знанием дела оценили все достоинства записи именно индийских чисел, а также смогли четко обозначить каждую цифру. Если в арабском тексте мы прочитаем цифры, то наверняка ошибемся. Ведь они пишут справа налево! Римские цифры, по мнению арабов, как и греческие, были неудобны, так как имели очень длинные записи. Когда было необходимо перемножить многозначные числа, то операция становилась невозможной, если запись выполняли при помощи греческой или римской нумерации.

Очень долгое время индийские цифры «кочевали» по разным странам, они претерпевали множество изменений в начертаниях, однако система исчисления остается прежней спустя столетия!

Возможно, многие считают, что арабские цифры придуманы арабами лишь только потому, что само слово «цифра» имеет арабские корни.

На сегодняшний день это вся информация. Возможно, археологи проведут какие-либо раскопки, которые прольют больше света на эту запутанную историю о древних цифрах.