Правило трех сигм 3. нормально распределение. кривая. правило трех сигм

σ цикл

Долгое время считалось, что σ-фактор обязательно покидает основной фермент, как только он инициирует транскрипцию, позволяя свободному σ-фактору связываться с другим основным ферментом и инициировать транскрипцию в другом сайте. Таким образом, σ-фактор переходит от одного ядра к другому. Однако Ричард Эбрайт и его коллеги, используя передачу энергии флуоресцентного резонанса, позже показали, что σ-фактор не обязательно покидает ядро. Вместо этого σ-фактор изменяет свою связь с ядром во время инициации и удлинения. Следовательно, σ-фактор циклически связывает между сильно связанным состоянием во время инициирования и слабосвязанным состоянием во время удлинения.

Практическое применение

На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.

Экономика и финансы

Среднее квадратическое отклонение доходности портфеля σ=DX{\displaystyle \sigma ={\sqrt {D}}} отождествляется с риском портфеля.

В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.

Климат

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой внутри континента. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

Обозначения

Прописная буква Σ обозначает:

Строчная σ обозначает:

• в теории вероятностей и математической статистике — среднеквадратичное отклонение (квадратный корень из дисперсии);
• в теории чисел — функцию суммы делителей числа ()
• в физике — удельную проводимость, тензор напряжений, коэффициент поверхностного натяжения или механическое напряжение;
• в химии — один из видов ковалентной связи и реакционную константу в уравнении Гаммета.
• в электронике существует Сигма-дельта модуляция.
• в астрономии — постоянная Стефана-Больцмана

С названием этой греческой буквы лишь опосредованно связаны названия сигмовидной кишки, а также графиков некоторых математических функций (сигмоиды): по форме они напоминают латинскую букву S.

Wikimedia Foundation . 2010 .

Смотреть что такое «Сигма (буква)» в других словарях:

СИГМА — 1) 18 я буква греческого алфавита, соответствует звуку с; 2) у древних римлян ложе для пиров, имевшее форму греческой буквы сигмы; 3) в мат. греч. сигма употр. для обозначения суммы и как знак интеграла. Словарь иностранных слов, вошедших в… … Словарь иностранных слов русского языка

Сигма — У этого слова несколько значений: Сигма буква греческого алфавита. Сигма (язык) Стандартное отклонение в теории вероятностей. Сигма алгебра в теории множеств. «Сигма» чешский футбольный клуб. Sigma Corporation японский производитель… … Википедия

буква — Знак (азбучный), письмена (множ. ч.), иероглиф (гиероглиф), каракуля, руны. Нагородил какие то каракули, и читай. .. Ср. знак. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. буква … Словарь синонимов

сигма — сумма, буква Словарь русских синонимов. сигма сущ., кол во синонимов: 2 • буква (103) • сумма … Словарь синонимов

СИГМА — (sigma) Буква греческого алфавита; заглавная изображается как Σ, строчная – как σ. В экономической литературе она используется различным образом. Заглавная буква Σ обычно обозначает сумму членов ряда: Σ1N x1=(x1+x2+. +xN) Здесь подстрочный… … Экономический словарь

СИГМА — греческая буква ?, ?. В математике символ ? часто употребляют для обозначения суммы … Большой Энциклопедический словарь

сигма — греческая буква Σ, Σ. В математике символ Σ часто употребляют для обозначения суммы. * * * СИГМА СИГМА, греческая буква S, s. В математике символ S часто употребляют для обозначения суммы … Энциклопедический словарь

СИГМА — греч. буква Г, о. В математике символ часто употребляют для обозначения суммы … Естествознание. Энциклопедический словарь

сигма — (др. греч. Σ, σ, ς σιγμα) 1) 18 я буква греческого алфавита; σ΄ – 200 ; ¸σ – 200000 ; 2) в математике: Σ – сумма … Словарь лингвистических терминов Т.В. Жеребило

сигма — (грч. sigma) назив за грчката буква … Macedonian dictionary

Шаги

Золотое правило нравственности

Часть 1 из 3:

Среднее значение

1. 1

   Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.
   X
   Источник информации

   • Определите количество чисел в наборе данных.
   • Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
   • Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
   • Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.

2. 2

   Для вычисления среднего значения понадобятся все числа данного набора данных.
   X
   Источник информации

   • Среднее значение – это усредненное значение всех чисел в наборе данных.
   • Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
   • В нашем примере (10, 8, 10, 8, 8, 4) n = 6.

3. 3

   Сложите все числа вашего набора данных.
   X
   Источник информации

   • В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
   • 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
   • Сложите числа еще раз, чтобы проверить ответ.

4. 4

   Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.
   X
   Источник информации

   • В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
   • В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
   • 48/6 = 8
   • Среднее значение данной выборки равно 8.

Часть 2 из 3:

Дисперсия

1

Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.
X
Источник информации

Эта величина даст вам представление о том, как разбросаны данные выборки.
Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.

2

Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.
X
Источник информации

В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
10 — 8 = 2; 8 — 8 = 0, 10 — 2 = 8, 8 — 8 = 0, 8 — 8 = 0, и 4 — 8 = -4.
Проделайте вычитания еще раз, чтобы проверить каждый ответ

Это очень важно, так как полученные значения понадобятся при вычислениях других величин.

3

Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.
X
Источник информации

При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
Возведите эти значения в квадрат: 22, 02, 22, 02, 02, и (-4)2 = 4, 0, 4, 0, 0, и 16.
Проверьте ответы, прежде чем приступить к следующему шагу.

4

Сложите квадраты значений, то есть найдите сумму квадратов.
X
Источник информации

В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
4 + 0 + 4 + 0 + 0 + 16 = 24.
Сумма квадратов равна 24.

5

Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке

Таким образом, вы получите дисперсию.
X
Источник информации

В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
n-1 = 5.
В нашем примере сумма квадратов равна 24.
24/5 = 4,8
Дисперсия данной выборки равна 4,8.

Часть 3 из 3:

Среднеквадратическое отклонение

1. 1

   Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.
   X
   Источник информации

   • Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
   • Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
   • В нашем примере дисперсия равна 4,8.

2. 2

   Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.
   X
   Источник информации

   • Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
   • В нашем примере дисперсия равна 4,8.
   • √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
   • 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).

3. 3

   Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.
   X
   Источник информации

   • Обязательно записывайте вычисления.
   • Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
   • Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.

Небольшой экскурс в историю качества

Многие связывают программу Шести сигма со стремлением улучшить качество. Рассматривать эту концепцию таким образом вполне логично, особенно в начале анализа проблем. Но Шесть сигма существенно отличаются от программ качества, с которыми вы, возможно, уже сталкивались. Чем? Чтобы ответить на этот вопрос, давайте кратко вспомним историю достижения высокого качества продукции.

В полной мере понять стремление добиться необходимого качества невозможно, если не вспомнить об идеях Эдвардса Деминга, хорошо известного своими разработками для Японии, которой он помог восстановить все отрасли экономики после Второй мировой войны. Его подход был совершенно новым для своего времени и оказал огромное воздействие на эволюцию качества и реализацию программ непрерывного совершенствования продукции в компаниях по всему миру.

Комплексное управление качеством (TQM – от английского Total Quality Management) – это управленческий подход, сосредоточенный на организации как системе, причем основное внимание уделяется командам, процессам, статистическим данным, постоянному совершенствованию, а также выпуску товаров и услуг, полностью удовлетворяющих ожидания потребителей или превосходящих их. Шесть сигма – это расширенный и более упорядоченный вариант TQM

Было бы справедливо упомянуть, что подход Деминга к управлению, также известный как «комплексное управление качеством» (хотя Демингу этот термин не нравился), изменил характер деятельности тысяч компаний и предопределил его на десятилетия вперед. К середине 1980-х годов масштабы, в которых корпоративное руководство занималось вопросами качества, стали совершенно иными: виды бизнеса, принявшие на вооружение TQM, трансформировались и отказались от всего, на что раньше делали ставку, перейдя к созданию более совершенных товаров и услуг. Руководители начали понимать, что качество вовсе не требует увеличения затрат, что более эффективные и надежные процессы позволяют добиваться отсутствия брака в готовой продукции и что им необходимо сосредоточиться на улучшении процесса производства и удовлетворения спроса потребителей. Словом, TQM – это отличный фундамент, на котором можно надежно строить следующий уровень управления качеством – подход по принципу Шести сигма.

Однако Шесть сигма – это не просто последняя модная новинка в борьбе за качество. Вам нужны доказательства? Компании, реализовавшие концепцию Шести сигма, добились отличных финансовых результатов и разработали более взвешенные, прагматичные планы, позволяющие им реально и существенно улучшить рентабельность бизнеса и добиться его расширения.

Такие компании, как «Motorola», «Texas Instruments», IBM, «AlliedSignal» и «General Electric», успешно реализовали концепцию Шести сигма и добились сокращения затрат на миллиарды долларов. Позже эту методологию приняли на вооружение «Ford», «DuPont», «Dow Chemical», «Microsoft» и «American Express». Причем, когда мы говорим об успехе, речь идет не только об экономии денег. Джек Уэлч, директор-распорядитель, начавший программу Шести сигма в «General Electric», назвал ее «наиболее важным проектом, когда-либо реализовывавшимся в GE», и заявил, что Шесть сигма – это «часть генетического кода нашего будущего лидерства».

Точных вам прогнозов и успехов!

Чем Forecast4AC PRO может вам помочь
при расчете доверительного интервала
?:

Forecast4AC PRO автоматически рассчитает верхнюю или нижнюю границы прогноза для более чем 1000 временных рядов одновременно;

Возможность анализа границ прогноза в сравнении с прогнозом, трендом и фактическими продажами на графике одним нажатием клавиши;

В программе Forcast4AC PRO есть возможность задать значение сигма от 1 до 3.

• Novo Forecast Lite

  — автоматический расчет прогноза
  в Excel

  .

• 4analytics — ABC-XYZ-анализ
  и анализ выбросов в Excel.

• Qlik Sense
  
  Desktop и QlikView

  Personal Edition — BI-системы для анализа и визуализации данных.

Тестируйте возможности платных решений:

Novo Forecast PRO

— прогнозирование в Excel для больших массивов данных.

Как известно, на рынках относительно часто нарушаются законы нормального распределения случайной величины: в каких-то инструментах чаще, в каких-то реже.

По моим наблюдениям, валютные пары менее подвержены нарушениям нормального распределения, чем акции или золото.

В золоте относительно часто происходят отклонения значения цены от нормального распределения на 3 или 4 средних квадратичных отклонения (сигмы).

Здесь, как говорят статистики, наибольшая дисперсия (разброс случайной величины).

Основной закон дисперсии:

Из неравенства Чебышёва следует, что вероятность того, что случайная величина отстоит от своего математического ожидания более чем на k стандартных отклонений, составляет менее 1/k². Так, например, как минимум в 95 % случаев случайная величина, имеющая нормальное распределение, удалена от её среднего не более чем на два стандартных отклонения, а в примерно 99,7 % — не более чем на три.

Приведу еще одну цитату из википедии

Правило трёх сигм (3σ) — практически все значения нормально распределённой случайной величины лежат в интервале (x¯−3σ;x¯+3σ). Более строго — приблизительно с 0,9973 вероятностью значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина x¯ истинная, а не полученная в результате обработки выборки).

На рисунке показан график USDJPY с нанесенными на нем 2σ и 3σ.

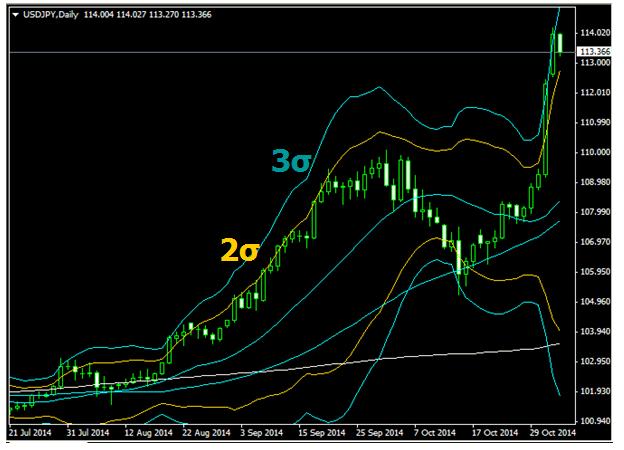
Как мы видим, пара достигла вчера значения сигма равного 3. Для валютного рынка это чересчур много и мы видим, что сегодня пара начала корректироваться вниз.

Теперь начинается консолидация, которая может затянуться очень надолго.

На мой взгляд ближайшие месяцы пара USDJPY проведет в коридоре 110-115. У меня очень большая уверенность, что до конца года USDJPY обязательно побывает в районе 110. Для этого есть много причин, о которых я напишу в других статьях.

3 сигмы на недельном графике AUDJPY

В продолжение темы о дисперсии приведу еще один рисунок. На нем показан недельный график AUDJPY.

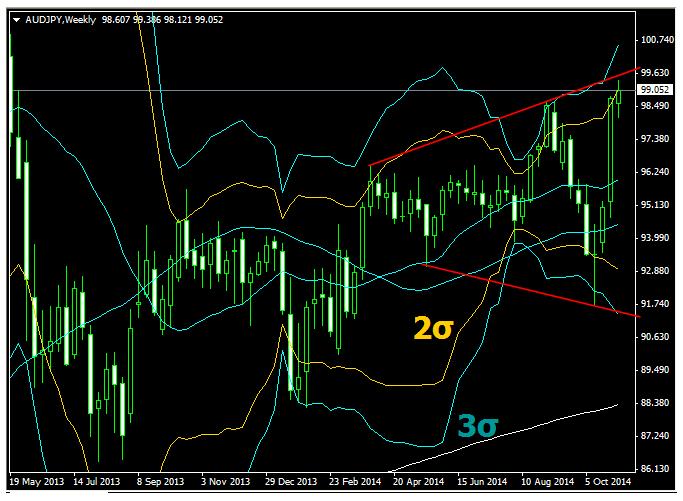
На нем очень хорошо видно, что вслед за касанием линии 3σ всегда происходит достаточно крупный разворот и пара проходила в противоположную сторону как минимум 7-8 фигур и это движение занимает много недель.

Если в ближайшие дни AUDJPY достигнет этого уровня, то с большой вероятностью можно ожидать повторения этого сценария.

Коэффициент вариации в статистике: примеры расчета

Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.

• Показатели описательной статистики
• Среднее арифметическое
• Стандартное отклонение
• Коэффициент вариации
• Расчёты в Microsoft Ecxel 2016

Среднее арифметическое

Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:

• Ширина интервала, куда попадает рост всех студентов, – 18 см.
• В распределении рост наиболее близок к середине этого интервала.
• Встречаются и исключения, которые наиболее близко расположены к верхней или нижней границе интервала.

Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться.

Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического.

Если обратиться к росту студентов, то формула будет выглядеть следующим образом:

Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)

Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).

Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.

Стандартное отклонение

Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.

На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:

Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:

Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:

Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.

Расчёты в Microsoft Ecxel 2016

Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:

Наименование показателя	Расчёт в Excel 2016*
Среднее арифметическое	=СРГАРМ(A1:A10)
Дисперсия	=ДИСП.В(A1:A10)
Среднеквадратический показатель	=СТАНДОТКЛОН.В(A1:A10)
Коэффициент вариации	=СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10)
Коэффициент осцилляции	=(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10)

* — в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.

Итак, обобщим информацию:

1. Среднее арифметическое – это значение, позволяющее найти среднее значение показателя в ряду данных.
2. Дисперсия – это среднее значение отклонений возведенное в квадрат.
3. Стандартное отклонение (среднеквадратичное отклонение) – это корень квадратный из дисперсии, для приведения единиц измерения к одинаковым со среднеарифметическим.
4. Коэффициент вариации – значение отклонений от среднего, выраженное в относительных величинах (%).

Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила — коэффициент вариации, который является мерой однородности данных.

Пояснения

Поскольку
⋂n=1∞An=X∖(⋃n=1∞(X∖An)),{\displaystyle \bigcap _{n=1}^{\infty }A_{n}=X\backslash \left(\bigcup _{n=1}^{\infty }(X\backslash A_{n})\right),}

в пункте 3, достаточно требовать, чтобы только пересечение или только объединение принадлежало S{\displaystyle {\mathfrak {S}}}.

• Для любой системы множеств S{\displaystyle {\mathcal {S}}} существует наименьшая сигма-алгебра σ(S){\displaystyle \sigma ({\mathcal {S}})}, являющаяся её надмножеством.
• Сигма-алгебры являются естественной областью определения . Если мера определена частично (на семействе множеств S{\displaystyle {\mathcal {S}}}) так, что выполнено условие сигма-аддитивности (синоним счётной аддитивности), эта частичная мера имеет единственное продолжение на σ(S){\displaystyle \sigma ({\mathcal {S}})}, то есть на наименьшую сигма-алгебру, это семейство содержащую, и при этом свойство сигма-аддитивности не нарушится.
• σ-алгебра, порождённая случайной величиной ξX→R{\displaystyle \xi :\,X\rightarrow \mathbb {R} }, определяется следующим образом:

σ(ξ)={ξ−1(B)∣B∈B(R)}{\displaystyle \sigma (\xi )=\left\{\xi ^{-1}(B)\mid B\in {\mathcal {B}}(\mathbb {R} )\right\}},

где B(R){\displaystyle {\mathcal {B}}(\mathbb {R} )} — борелевская сигма-алгебра на вещественной прямой. Это — наименьшая сигма-алгебра на пространстве X{\displaystyle X}, относительно которой случайная величина ξ{\displaystyle \xi } всё ещё остаётся измеримой. Эта же конструкция применяется и в том случае, если на пространстве X{\displaystyle X} вообще не выделена никакая сигма-алгебра, в этом случае с помощью функции ξ{\displaystyle \xi } её можно ввести и наделить таким образом пространство X{\displaystyle X} структурой измеримого пространства, так что функция ξ{\displaystyle \xi } будет измеримой.

Как работает стандартное отклонение в Excel

      Добрый день!

     В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику.

А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается.

В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.

В Excel используются несколько вариантов этой функции отклонения:

• Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
• Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
• Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
• Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.

Математическая теория

      Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.

     Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!

     Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так:      Отмечу, что все две оценки предоставляются смещёнными. При общих случаях построить несмещённую оценку не является возможным. Но оценка на основе оценки несмещённой дисперсии будет состоятельной.

Практическое воплощение в Excel

     Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.

      Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:

        =СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:

Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.

      Теперь создадим файл примера и на его основе рассмотрим работу этой функции.

     Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц.

Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.

    Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4).       Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода.

Получится формула следующего вида: =СТАНДОТКЛОН.Г(C4;D4;E4).      Ну вот и сделана половина дел. Следующим шагом мы формируем «Вариацию», это получается делением на среднее значение, стандартного отклонения и результат переводим в проценты.

Получаем такую таблицу:        Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно.

Для получения результата по условиям воспользуемся логической функцией ЕСЛИ и для получения результата напишем формулу:

                =ЕСЛИ(H4

Математическое ожидание

Среднее значение можно вычислить не только для выборки, но для случайной величины, если известно ее распределение. В этом случае среднее значение имеет специальное название – Математическое ожидание. Математическое ожидание характеризует «центральное» или среднее значение случайной величины.

Примечание: В англоязычной литературе имеется множество терминов для обозначения математического ожидания: expectation, mathematical expectation, EV (Expected Value), average, mean value, mean, E или first moment M.

Если случайная величина имеет дискретное распределение, то математическое ожидание вычисляется по формуле:

где x_i – значение, которое может принимать случайная величина, а р(x_i) – вероятность, что случайная величина примет это значение.

Если случайная величина имеет непрерывное распределение, то математическое ожидание вычисляется по формуле:

где р(x) – плотность вероятности (именно плотность вероятности, а не вероятность, как в дискретном случае).

Для каждого распределения, из представленных в MS EXCEL, Математическое ожидание можно вычислить аналитически, как функцию от параметров распределения (см. соответствующие статьи про распределения). Например, для Биномиального распределения среднее значение равно произведению его параметров: n*p (см. файл примера ).

Функция СРОТКЛ в Excel используется для анализа числового ряда, передаваемого в качестве аргумента, и возвращает число, соответствующее среднему значению, рассчитанному для модулей отклонений относительно среднего арифметического для исследуемого ряда.

Структура

Sigma70 region 1.1
Идентификаторы
Символ	Sigma70_r1_1
Pfam
InterPro
Доступные структуры белков
Pfam
PDB
PDBsum

Sigma70 region 1.2
Crystal structure of Thermus aquaticus RNA polymerase sigma subunit fragment containing regions 1.2 to 3.1
Идентификаторы
Символ	Sigma70_r1_2
Pfam
InterPro
PROSITE
SCOP
SUPERFAMILY
Доступные структуры белков
Pfam
PDB
PDBsum

Sigma70 region 2
Crystal structure of a sigma70 subunit fragment from Escherichia coli RNA polymerase
Идентификаторы
Символ	Sigma70_r2
Pfam
Pfam clan
InterPro
PROSITE
SCOP
SUPERFAMILY
Доступные структуры белков
Pfam
PDB
PDBsum

Sigma70 region 3
Solution structure of sigma70 region 3 from Thermotoga maritima
Идентификаторы
Символ	Sigma70_r3
Pfam
Pfam clan
InterPro
SCOP
SUPERFAMILY
Доступные структуры белков
Pfam
PDB
PDBsum

Sigma70 region 4
Solution structure of sigma70 region 4 from Thermotoga maritima
Идентификаторы
Символ	Sigma70_r4
Pfam
Pfam clan
InterPro
SCOP
SUPERFAMILY
Доступные структуры белков
Pfam
PDB
PDBsum

Sigma70 region 4.2
Crystal structure of Escherichia coli sigma70 region 4 bound to its -35 element DNA
Идентификаторы
Символ	Sigma70_r4_2
Pfam
Pfam clan
InterPro
SCOP
SUPERFAMILY
Доступные структуры белков
Pfam
PDB
PDBsum

Сигма факторы имеют четыре основные части, которые обычно присутствуют во всех сигма факторах:

N-terminus --------------------- C-terminus
             1.1    2    3    4

Основные части дополнительно подразделяются (например, 2 включает в себя 2.1, 2.2 и т. Д.)

• Область 1.1 обнаруживается только в «первичных сигма факторах» (RpoD, RpoS в Кишечной палочке). Он обеспечивает связываемость сигма-фактора с промотором только тогда, когда он находится в комплексе с РНК-полимеразой.
• Регион 2.4 распознает и связывается с промотором -10 (он называется «Прибнов-бокс»).
• Регион 4.2 распознает и связывается с промотором -35.

Единственным исключением из этой правила является сигма-фактор типа σ54 . Белки, гомологичные σ54 RpoN, являются функциональными сигма-факторами, но имеют существенно отличающиеся первичные аминокислотные последовательности.