§ 5. логические отношения между понятиями

СОВМЕСТИМЫЕ И НЕСОВМЕСТИМЫЕ ПОНЯТИЯ. ИХ РАЗНОВИДНОСТИ.

Поможем написать любую работу на аналогичную
тему

• Реферат

  От 250 руб

• Контрольная
  работа

  От 250 руб

• Курсовая работа

  От 700 руб

Получить выполненную работу или консультацию специалиста по вашему
учебному проекту

Узнать стоимость

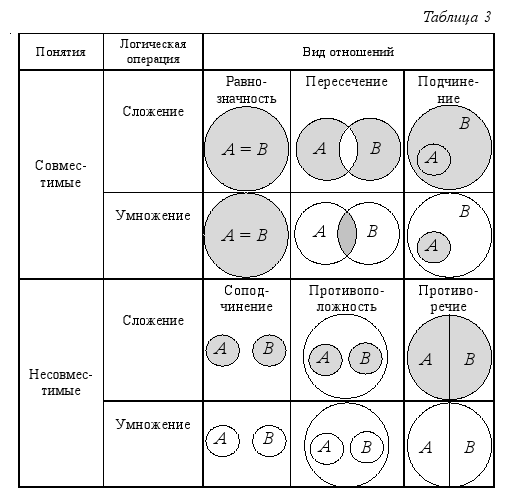
Отношения между понятиями по объёму возможны лишь между сравнимыми понятиями – это такие понятия, в содержании которых имеются общие признаки. Несравнимые – это такие понятия, в содержании которых не имеются общие признаки для сравнения.

Сравнимые делятся на: Совместимые и Несовместимые.

Совместимые – это такие понятия, объёмы которых содержат общие элементы.

Несовместимые – это такие понятия, объёмы которых не содержат общие элементы.

Виды совместимости:

1.                      Равнозначность – отображаются посредством кругов схем на плоскости. Равнозначность имеет место между такими понятиями, содержание которых различно, но объёмы совпадают (студент и учащийся в высшей школе).(рис 1)

2.                      Подчинение – когда объём одного понятия, полностью включает в себя объём другого, например А – учащийся, В – студент. Пересечение –имеет место в случаях, когда объёмы понятий совмещены частично, например, понятия А – студент, В — гурман.

Виды несовместимости:

1.                      Соподчинение – имеет место как минимум между тремя понятиями. Одно из которых является родовым, а остальные видами данного рода, не находящимися в состоянии пересечения. А –дерево, В – дуб, С – берёза, Е –ель. Понятие А – находится в состоянии подчинения ко всем остальным, они подчиняющее. В, С, Е – в состоянии соподчинения между ними нет общих элементов.)

2.                      Противоречие – имеет место, когда одно понятие утверждает наличие каких-либо признаков, а другое понятие эти признаки отрицает. Противоречивое понятие выражается отрицательными частицами. Сумма объёмов противоречивых понятий равна объёму родового понятия. А – белый, Не А – не белый. Изображается с черточкой сверху Ā.

Противоположность – имеет место, когда одно понятие содержит какие-либо признаки предмета, а другое – их отрицает, заменяя на противоположное понятие. Сумма объёмов противоположных понятий не исчерпывает объёма родового понятия. Хороший – Плохой, Белый – Чёрный.

Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас

Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.

Расчет
стоимостиГарантииОтзывы

1.5. Операция определения понятия

   
Определение понятия– это логическая операция, которая раскрывает содержание понятия.   Определения бывают явными и неявными.   
Явноеопределение непосредственно раскрывает содержание понятия, даёт прямой ответ на вопрос, чем является объект, который оно обозначает. Например: «
Термометр – это физический прибор, предназначенный для измерения температуры», – явное определение.   
Неявное
(контекстуальное)определение раскрывает содержание понятия не прямо, а косвенно, с помощью контекста, в котором это понятие употребляется. Например, из следующей фразы: «
Во время этого грандиозного эксперимента сверхточные термометры зафиксировали температуру в 1 000 °C», – косвенно следует ответ на вопрос: «Что такое термометр?» – вытекает неявное определение этого понятия. Понятно, что определениями в полном смысле этого слова надо считать явные определения. В дальнейшем речь пойдёт именно о них.   Определения также бывают реальными и номинальными.   
Реальноеопределение раскрывает содержание понятия, обозначающего какой-то объект, т. е. они посвящены объектам. Например:   «
Термометр – это физический прибор, предназначенный для измерения температуры» – реальное определение.   
Номинальное(от лат. nomen – имя) раскрывает значение термина, которым выражено какое-либо понятие, т. е они посвящены терминам (словам). Например: «
Слово «термометр» обозначает физический прибор, предназначенный для измерения температуры», – номинальное определение.   Как видим, принципиальной разницы между реальными и номинальными определениями не существует. Они различаются, как правило, по форме, но не по сути.   Существует несколько способов определения понятия, но среди них выделяется классический способ, который заключается в том, что определяемое понятие подводится под ближайшее к нему родовое понятие, после чего следует указание на его видовое отличие. Например, определение: «
Астрономия – это наука о небесных телах», – построено по классическому способу. В нём определяемое понятие «
астрономия» сначала подводится под ближайшее к нему родовое понятие «
наука» (астрономия – это обязательно наука, но наука – это не обязательно астрономия), а потом указывается на видовое отличие астрономии от других наук: «…
о небесных телах». Пользуясь классическим способом, вы сможете дать точное и правильное определение любому понятию, конечно, если определяемый объект или термин вам хорошо знаком, и вы знаете, что он собой представляет или что означает, соответственно. Например, нам требуется дать определение понятию «
квадрат». Следуя классическому способу, сначала подведём его под родовое понятие: «
Квадрат – это геометрическая фигура», – а затем укажем его видовое отличие от других геометрических фигур, которое заключается в наличии
равных сторон и прямых углов. Итак: «
Квадрат – это геометрическая фигура, у которой все стороны равны и углы прямые». Давая определение понятию «
квадрат», мы могли бы подвести его под более близкое родовое понятие «
прямоугольник», и тогда определение получилось бы следующим: «
Квадрат – это прямоугольник, у которого все стороны равны», – однако и приведённое выше определение квадрата раскрывает содержание соответствующего понятия и является верным

Обратите внимание на то, что фактически все определения, встречающиеся в научной, учебной и справочной литературе, например в толковых словарях, построены по классическому способу.   Существует несколько логических правил определения. Нарушение хотя бы одного из них приводит к тому, что содержание понятия не раскрывается и определение не достигает своей цели, являясь неверным

Рассмотрим эти правила и ошибки, возникающие при их нарушении:   1.
Определение не должно быть широким, т. е. определение не должно превышать своим объёмом определяемое понятие. Например, определение: «
Солнце – это небесное тело», – является
широким: определение «
небесное тело» по объёму намного больше определяемого понятия «
Солнце». Из приведённого определения не вполне понятно, что такое Солнце, ведь небесное тело – это и планета, и комета и т. п. В данном случае можно также сказать, что, пользуясь классическим способом определения, мы подвели определяемое понятие «
Солнце» под родовое понятие «
небесное тело», но не сделали второй шаг – не указали на его видовое отличие.   2.
Определение не должно быть узким, т. е. определение не должно быть по своему объёму меньше определяемого понятия. Например, определение: «

Отношение между понятиями. Совместимые и несовместимые понятия. Сравнимые и несравнимые понятия.

Поможем написать любую работу на аналогичную
тему

• Реферат

  От 250 руб

• Контрольная
  работа

  От 250 руб

• Курсовая работа

  От 700 руб

Получить выполненную работу или консультацию специалиста по вашему
учебному проекту

Узнать стоимость

Объективные отношения между самими предметами находят свое отражение в отношениях между понятиями. Все многообразие этих отношений также можно классифицировать на основе содержания и объема понятий.

Сравнимые и несравнимые понятия. Сравнимыми называют понятия, в содержании которых имеется хотя бы один общий признак. Почти все понятия являются сравнимыми. В данном случае опровергается известная пословица «Нельзя сравнивать Божий дар с яичницей». С точки зрения логики, это также сравнимые понятия, так как о них, по крайней мере, можно сказать, что и то, и другое – предмет. Это и будет их общий признак. Несравнимыми называют понятия, в содержании которых нет ни одного общего признака. Некоторые авторы в качестве примера несравнимых понятий приводят понятия «предмет» и «свойство». Сравнимые понятия могут быть совместимыми или несовместимыми.

Совместимые и несовместимые понятия. Понятия называются совместимыми, если их объемы имеют хотя бы один общий элемент. Несовместимые – это понятия, в объемах которых нет ни одного общего элемента. Обычно отношения между понятиями изображают с помощью так называемых кругов Эйлера (рис. 2, 3).

Виды совместимых понятий. Совместимые понятия могут быть равнозначными (тождественными), перекрещивающимися, а также подчиненным и подчиняющим.

Равнозначные (тождественные) — это понятия, объемы которых полностью совпадают (рис. 2, а).

Пример. А – понятие «автор романа «Анна Каренина»»; В – понятие «автор романа «Война и мир»».

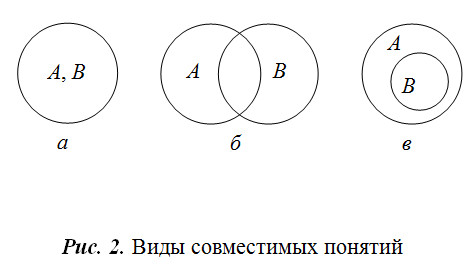
Перекрещивающиеся — это понятия, объемы которых частично совпадают (рис. 2, б).

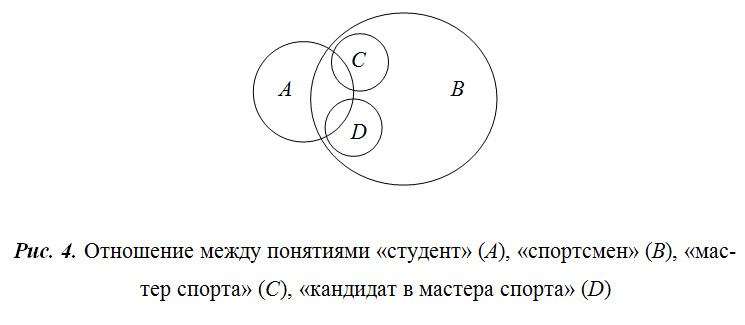
Пример. А – понятие «студент»; В – понятие «спортсмен».

Подчиняющее и подчиненное понятия. Объем подчиненного понятия полностью входит в объем подчиняющего, не исчерпывая его (рис. 2, в).

Пример. А – понятие «деревья»; В – понятие «береза».

Виды несовместимых понятий. Несовместимые понятия бывают соподчиненными, противоположными (контрарными) и противоречащими (контрадикторными).

Соподчиненные – это понятия, объемы которых различны и входят в объем общего для них понятия, не исчерпывая его (рис. 3, а).

Пример. А – понятие «фиалка»; В – понятие «роза»; С – понятие «цветы».

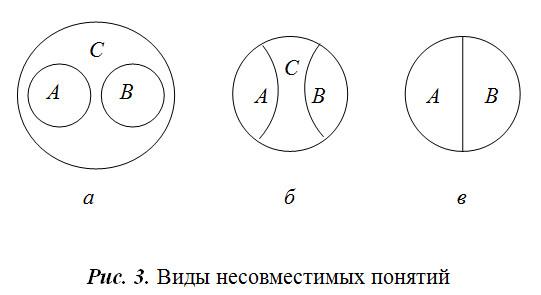
Противоположными (контрарными) понятиями являются такие, которые соподчинены третьему понятию и представляют собой крайние степени выраженности некоторого качества. Можно сказать, что их объемы занимают полярные места в объеме общего для них понятия (рис. 3, б).

Пример. А – «черный»; В – «белый»; С – «цвет».

Противоречивые (контрадикторные) понятия подчиняются общему для них понятию, и при этом в общем понятии не существует такого элемента, который не был бы элементом одного из этих понятий. Их объемы делят объем общего для них понятия на две части (рис. 3, в).

Пример. А – «монархия»; В – «республика». Общим для этих понятий является понятие «форма правления». Причем «монархия» и «республика» – несовместимые формы правления, и в то же время других форм правления не существует.

С помощью кругов Эйлера можно получать достаточно сложные схемы. Например, можно изобразить отношение между понятиями А – «студент», В – «спортсмен», С – «мастер спорта», D – «кандидат в мастера спорта» (рис. 4).

Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас

Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.

Расчет
стоимостиГарантииОтзывы

Изучение отношений между понятиями имеет огромное значение для правильного употребления понятий в устной и письменной речи. И наоборот, незнание этих отношений способно повлечь за собой искаженное отражение действительности – отношений между самими вещами.

Функции и законы

Итак, мы уже знаем, какие логические операции использует булева алгебра. Функции описывают все свойства элементов математической логики и позволяют упрощать сложные составные условия задач. Самым понятным и простым кажется свойство отказа от производных операций. Под производными понимаются исключающее ИЛИ, импликация и эквивалентность. Поскольку мы ознакомились только с основными операциями, то и свойства рассмотрим тоже только их.

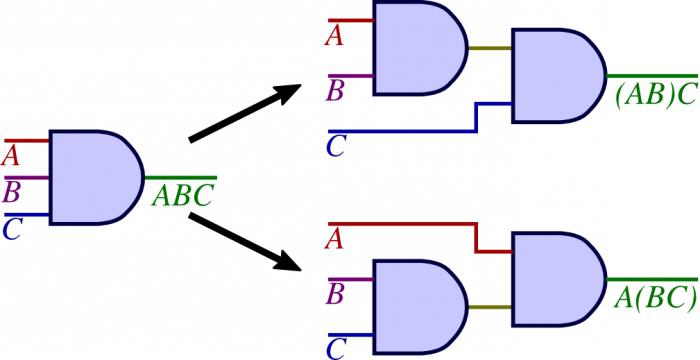
Ассоциативность означает, что в высказываниях типа «и А, и Б, и В» последовательность перечисления операндов не играет роли. Формулой это запишется так:

(A∧Б)∧В=A∧(Б∧В)=A∧Б∧В,

(A∨Б)∨В=A∨(Б∨В)=A∨Б∨В.

Как видим, это свойственно не только конъюнкции, но и дизъюнкции.

Коммутативность утверждает, что результат конъюнкции или дизъюнкции не зависит от того, какой элемент рассматривался вначале:

A∧Б=Б∧A; A∨Б=Б∨A.

Дистрибутивность позволяет раскрывать скобки в сложных логических выражениях. Правила схожи с раскрытием скобок при умножении и сложении в алгебре:

A∧(Б∨В)=A∧Б∨A∧В; A∨Б∧В=(A∨Б)∧(A∨В).

Свойства единицы и нуля, которые могут быть одним из операндов, также аналогичны алгебраическим умножению на ноль или единицу и сложению с единицей:

A∧0=0,A∧1=A; A∨0=A,A∨1=1.

Идемпотентность говорит нам о том, что если относительно двух равных операндов результат операции оказывается аналогичным, то можно «выбросить» лишние усложняющие ход рассуждений операнды. И конъюнкция, и дизъюнкция являются идемпотентными операциями.

Б∧Б=Б; Б∨Б=Б.

Поглощение также позволяет нам упрощать уравнения. Поглощение утверждает, что когда к выражению с одним операндом применяется другая операция с этим же элементом, результатом оказывается операнд из поглощающей операции.

A∧Б∨Б=Б; (A∨Б)∧Б=Б.

Совместимые понятия

Отношения совместимости могут быть трех видов. Сюда входят равнозначность, перекрещивание и подчинение.

Равнозначность. Отношение равнозначности иначе называется тождеством понятий. Оно возникает между понятиями, содержащими один и тот же предмет. Объемы этих понятий совпадают полностью при разном содержании. В этих понятиях мыслится либо один предмет, либо класс предметов, содержащий более чем один элемент. Говоря более просто, в отношении равнозначности находятся понятия, в которых мыслится один и тот же предмет.

В качестве примера, иллюстрирующего отношения равнозначности, можно привести понятия «равносторонний прямоугольник» и «квадрат». В этих понятиях содержится отражение одного и того же предмета – квадрата, значит, объемы этих понятий полностью совпадают. Однако содержание их различно, потому что каждое из них содержит разные признаки, характеризующие квадрат. Отношение между двумя подобными понятиями на круговой схеме отражается в виде двух полностью совпадающих кругов (рис. 1).

Пересечение (перекрещивание). Понятиями, находящимися в отношении пересечения, признаются те, объемы которых совпадают частично. Объем одного, таким образом, частично входит в объем другого и наоборот. Содержание таких понятий будет разным. Схематичное отражение отношение пересечения находит в виде двух частично совмещенных кругов (рис. 2). Место пересечения на схеме для удобства штрихуется. Примером могут служить понятия «селянин» и «тракторист»; «математик» и «репетитор». Та часть круга А, которая не пересечена с кругом В, содержит отражение всех селян – не трактористов. Та часть круга В, которая не пересечена с кругом А, содержит отражение всех трактористов, которые не являются селянами. В месте пересечения кругов А и В мыслятся селяне-трактористы. Таким образом, получается, что не все селяне есть трактористы и не все трактористы являются селянами.

Подчинение (субординация). Отношение субординации характерно тем, что объем одного понятия полностью входит в объем другого, но не исчерпывает его, а составляет лишь часть.

Это отношения род – > вид – > индивид.

В таком отношении находятся, к примеру, понятия «планета» и «Земля»; «спортсмен» и «боксер»; «ученый» и «физик». Как несложно заметить, здесь объем одних понятий шире, чем других. Ведь Земля суть планета, но не каждая планета является Землей. Кроме Земли есть еще Марс, Венера, Меркурий и еще множество планет, в том числе неизвестных человеку. Та же ситуация возникает и в других приведенных примерах. Не каждый спортсмен – боксер, но боксер – это всегда спортсмен; любой физик есть ученый, но, говоря об ученом, мы не всегда подразумеваем физика и т. д. Здесь одно из понятий является подчиненным, другое – подчиняющим. Очевидно, что подчиняет понятие, имеющее больший объем. Подчиняющее понятие обозначается буквой А, подчиненное – буквой В.

На схеме отношение подчинения отображается в виде двух кругов, один из которых вписан в другой (рис 3).

Когда в отношение подчинения входит два понятия, каждое из которых является общим (но не единичным), понятие А (подчиняющее) становится родом, а В (подчиненное) – видом. То есть понятие «планета» будет родом для понятия «Земля», а последнее есть вид. Бывают случаи, когда отдельное понятие может быть одновременно и родом, и видом. Это происходит, если понятиерод, содержащее в себе понятие-вид, относится к третьему понятию, которое шире последнего по объему. Получается тройное подчинение, когда более общее понятие подчиняет менее общее, но одновременно находится в отношении подчинения с другим, имеющим больший объем. В качестве примера можно привести следующие понятия: «биолог», «микробиолог» и «ученый». Понятие «биолог» является подчиняющим по отношению к понятию «микробиолог», но подчинено понятию «ученый».

Возможна ситуация, когда в отношение подчинения вступают общее и единичное понятия. В этом случае общее и по совместительству подчиняющее понятие является видом. Единичное понятие становится по отношению к общему индивидом. Такой вид отношения иллюстрирует подчинение понятия «Земля» понятием «планета». Также можно привести следующий пример: «русский писатель» – «Н. Г. Чернышевский».

Таким образом, отношение подчинения упрощенно можно отразить в линейных схемах: «род – > вид – > вид».

Забегая вперед, можно отметить, что отношение «род – > вид – > индивид» используется в таких логических операциях с понятиями, как обобщение, ограничение, определение и деление.

Виды совместимости понятий

1) Тождество (равнообъемность, равнозначность)

В отношении тождества находятся такие понятия, объемы которых полностью совпадают.

Например:

Москва (А), Столица России (В);

Преступление (А), Общественно опасное деяние (В).

2) Пересечение

В отношении пересечения находятся понятия, объемы которых частич­но совпадают.

Преподаватель (А), Женщина (В).

Не каждый преподаватель является женщиной. Так же как и не каждая женщина является препо­давателем, но есть такие преподаватели, которые одновременно являются женщинами.

3) Подчинение

В отношении подчинения находятся такие понятия, объем одного из ко­торых полностью входит в объем другого, но не исчерпывает его.

При этом понятие с большим объемом (ро­довое) называется подчиняющим (А), понятие с меньшим объемом (видовое) – подчиненным (В).

Преступление (А), Кража (В).

Виды несовместимости понятий

1) Соподчинение

В отношении соподчинения находятся два или более непересекающихся понятия, принадлежащих общему родовому понятию. Другими словами, это отношение двух и более видов к одному роду.Дерево (А) Сосна (В) Береза (С)

2) Противоположность

В отношении противоположности находятся понятия, которые явля­ются видами одного и того же рода, при этом одно из них содержит какие-то признаки, а другое эти признаки исключает и заменяет противоположными признаками.

Объемы понятий (В и С) в объеме родового по­нятия (А) занимают наиболее удаленные части.Чай (А) Горячий (В) Холодный (С)

В сумме объемы противоположных понятий не исчерпывают объем родо­вого понятия. В середине круга оставлено место для любого другого среднего, промежуточного понятия. Например, понятия «правда» и «ложь» являются противоположными понятиями, но между ними может быть понятие «заблуж­дение», которое является промежуточным.Противоположные понятия можно рассматривать как соподчиненные.

3) Противоречие

В отношении противоречия находятся такие два понятия, которые являются видами одного и то­го же рода, при этом одно понятие указывает на не­которые признаки, а другое эти признаки исключает, но ничем другим не заменяет.

Виновный (А) Невиновный (не-А)

Для чего необходимо уметь правильно соотносить объемы понятий?

Имея представление о соотношении понятий, человек верно строит с ни­ми суждения.

Например, как соотносятся между собой понятия «преступник» и «нар­коман»? Отношение пересечения, но никак не подчинение. Отсюда следует, что суждение «Все наркоманы преступники» – ложно.

Виды понятий

Среди понятий выделяют определенные виды. Виды понятийвыделяют по двум основаниям: по качеству, или содержанию и по количеству, или объему.

По количеству понятия делят на простые, сложные и дескриптивные;единичные, общие и пустые; регистрирующие и нерегистрирующие:

–       простые выражаются одним словом («республика», «гражданство», «кодекс», «совесть»);

–       сложные выражаются словосочетанием из двух слов («столица республики», «гражданское право», «кодекс чести», «свобода совести»);

–       дескриптивные, или описательные выражаются словосочетанием из трех и более слов («абсолютно черное тело», «редкие свойства души»);

–       единичные – это понятия, в которых мыслится лишь один элемент определенного класса («столица Украины», «студент I курса Иванов»);

–       общие – это понятия, в которых мыслитсямножество элементов определенного класса («страна», «государство», «экономист», «автомобиль»);

–       пустые – это понятия, в которых мыслится множество, не содержащее ни одного элемента (пустое множество) («философский камень», «кентавр», «вечный двигатель», «золотой век», «идеальный газ»);

–       регистрирующие – это понятия, объем которых представляет собой конечное множество элементов, количество которых может быть точно определено («государства-члены ООН», «вес человека»);

–        нерегистрирующие – это понятия, объем которых представляет собой бесконечное множество элементов либо количество этих элементов практически определить невозможно («человек», «улика», «ум»).

По качеству понятия делят на положительные (позитивные) и отрицательные (негативные), конкретные и абстрактные, соотносительные и безотносительные, собирательные и несобирательные (разделительные):

–       позитивные – это понятия, в содержании которых мыслится присущий предмету определенный признак («вежливый», «моральный», «алчный», «ненастный», «безупречный», «беспечный»);

–       негативные – это понятия, в содержании которых фиксируется отсутствие у предмета хотя бы одного признака («невежливый», «аморальный», «безграмотный», «некрасивый», «бескорыстный»);

–       конкретные – это понятия, элементами объема которых являются реальные, самостоятельно существующие предметы («справедливый руководитель», «поэма В. Маяковского «Хорошо!»», «свидетель», «субботник», «развитие», «зачетно-экзаменационная сессия»);

–       абстрактные отражают свойства предметов или отношения между ними и не существуют отдельно от них («гениальный», «справедливый», «честный», «тождество», «неравенство», «причинность»);

–       соотносительныеотражают предметы, существование которых немыслимо без существования некоторых других предметов («дебет – кредит», «брат – сестра», «начальник – подчиненный»);

–       безотносительныеотражают предметы, которые существуют самостоятельно и не нуждаются для своего понимания в наличии другого понятия («человек», «дом», «книга», «банк», «город»);

–       собирательные отражают совокупность однородных предметов, мыслимых как единое целое (общие – «созвездие», «библиотека»; единичные – «созвездие «Большая Медведица»», «библиотека им. Н. К. Крупской»);

–       несобирательные – это понятия, содержание которых можно отнести и ко всем элементам определенного множества (класса), и к каждому элементу в отдельности, мыслимого в понятии («вуз», «ручка», «река», «игрушка»). Единичные понятия разделительными быть не могут, т.к. в них мыслится только один элемент, а по отношению к нему квантор общности неприменим.

Так, отталкиваясь от выше изложенного, может быть дана полная логическая характеристика, например, понятия «мировоззрение»: по количеству выражающих слов – это простое понятие, по объему – общее, нерегистрирующее, по содержанию – позитивное, конкретное, безотносительное, разделительное.

Исходя из контекста употребления того или иного понятия в предложении, можно определить, или это понятие является универсальным, или неуниверсальным. Универсальным является понятие, если оно употреблено в своем сущностном общем значении. В универсальные понятия входят все предметы, рассматриваемые в данной области знания или в пределах данных рассуждений («натуральные числа – в арифметике», «растения – в ботанике»). Понятие, употребленное не в своем сущностном общем значении, – неуниверсально.