Круги эйлера и примеры задач на логику

Задачи на делимость (сложная делимость)

Это задачи уже повышенной сложности. Предварительно советуем изучить тему «делимость». Обязательно к прочтению только тем, кто собирается занимать призовые места.

Для скольких чисел между и верно следующее утверждение: число делится на или не делится на ?

Такое страшное и непонятное условие становится простым, если воспользоваться кругами Эйлера. Понятно, что в этой задаче рассматриваются числа, которые — нас интересуют те, что внутри соответствующего круга. Также есть числа, которые vdots 12 — нас интересуют числа, которые вне. А что же с числами, которые принадлежат обоим множествам? Во-первых, каким общим свойством они обладают, а во-вторых, интересуют ли они нас?

Сначала ответим на первый вопрос. Оказывается, если число одновременно делится на два других числа, то оно делится на Наименьшее Общее Кратное этих двух чисел, то есть на минимальное число, которое делится без остатка на оба исследуемых. Для чисел и НОК есть ничто иное, как число , так как и , а меньше числа с такими свойствам нет. Итого, в пересечении наших множеств лежат числа, которые .

«ИЛИ»

Итак, диаграмма Эйлера-Венна выглядит следующим образом:
Штриховкой обозначены те числа, которые и надо найти. Теперь, надеюсь, очевидно, что нам необходимо найти, сколько всего числе в рассматриваемой задаче, из этого количества вычесть количество чисел, которые и прибавить количество чисел, которые .

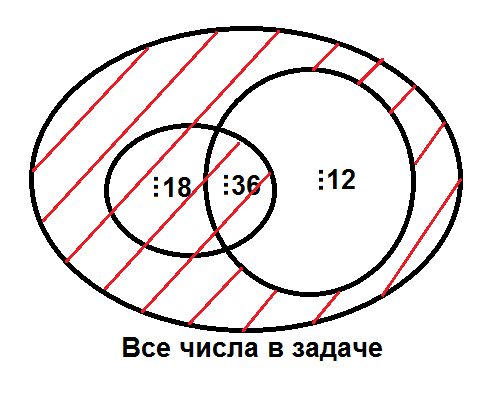
Итак, приступим:

1. В задаче рассматриваются числа между и . Это значит, что мы имеем дело с числами . Это подряд идущие числа, а, значит, их количество
2. Числа, которые : . Уменьшим их всех в раз. Получится новый ряд с таким же количеством чисел: . Это уже подряд идущие числа. Их .
3. Числа, которые vdots : . Уменьшим их в раз. Получится новый ряд с таким же количеством чисел: . Это подряд идущие числа. Их .

Итак, подведём итог. Если Вы собираетесь поступать в 5 класс физико-математического лицея, то общие знания по кругам Эйлера-Венна Вам необходимы. Основная область применения — задачи, где присутствуют множества объектов, обладающих определёнными свойствами, и необходимо найти количество объектов обладающих (или не обладающих) совокупностью указанных свойств.

Пример решения задачи с помощью кругов Эйлера

58 человек ежедневно добираются на работу общественным транспортом: на автобусе, на трамвае или на метро. Каждый пользуется хотя бы одним из видов транспорта. 42 человека из них используют метро, 32 – трамвай, 44 – автобус. 21 человек из них используют метро и трамвай, 31 – метро и автобус, 22 – трамвай и автобус. Сколько среди них человек, которые используют все три вида транспорта, чтобы добраться на работу?

Тут нужно понимать, что если сказано, что «42 человека используют метро», то это вовсе не означает, что кроме метро они не используют никаких других видов транспорта. Кто-нибудь из них может быть и использует. Может быть ещё какой-то один вид транспорта, трамвай или автобус. А может и сразу оба! Вопрос задачи как раз и состоит в том, чтобы посчитать людей, которые используют все три вида транспорта.

С первого взгляда даже непонятно, с чего начинать решение. Но если немного поразмыслить, становится ясно, что действовать нужно по следующему алгоритму. Будем стараться расписать всех людей (58 человек) через известные из условия данные. Нам известно, что автобус используют 44 человека. Прибавим к этому количество людей, которые используют метро. Их всего 42 человек. С помощью кругов Эйлера эту операцию можно изобразить наглядно в следующем виде:

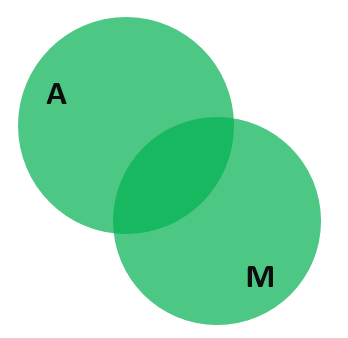
То есть пока что мы имеем дело с выражением 58 = 44 + 42… Знак «…» означает, что выражение ещё не закончено. Проблема в том, что мы посчитали людей на пересечении этих кругов дважды. Соответствующая область на диаграмме выделена тёмно-зелёным цветом. Поэтому один раз их нужно вычесть. Это люди, которые пользуются автобусом и метро. Их, как известно, 31. То есть наше «неоконченное» выражение принимает вид: 58 = 44 + 42 — 31… И на диаграмме при этом пропадает тёмно-зелёный цвет:

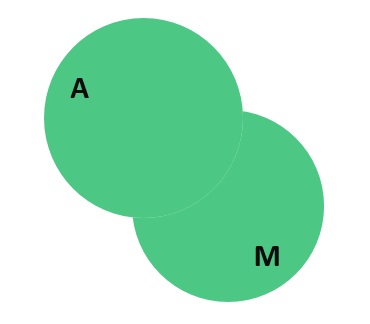
Пока всё хорошо. Прибавляем теперь людей, которые ездят на трамвае. Таких людей 32. Выражение принимает вид: 58 = 44 + 42 — 31 + 32… Диаграмма с кругами Эйлера, в свою очередь, становится следующей:

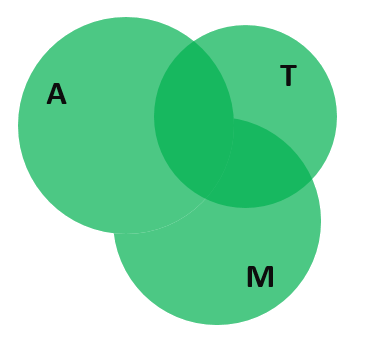
Проблема в том, что опять мы хватанули лишку. Люди, которых мы вновь посчитали дважды, отмечены на диаграмме тёмно-зелёным цветом. Эта область находится на пересечении множества, которое мы получили на предыдущем этапе, и множества людей, пользующихся трамваем.

Нужно вычесть людей, которых мы посчитали дважды. Но как это сделать? Единственное, что мы можем сделать, — это разом вычесть людей, которые передвигаются на трамвае и автобусе (их 22 человека), а также на трамвае и метро (таких людей 21). После этого наше неоконченное выражение для общего количества людей примет вид: 58 = 44 + 42 — 31 + 32 — 22 — 21…, а диаграмма с кругами Эйлера окажется с дыркой в центре, потому что центральную часть мы вычли дважды:

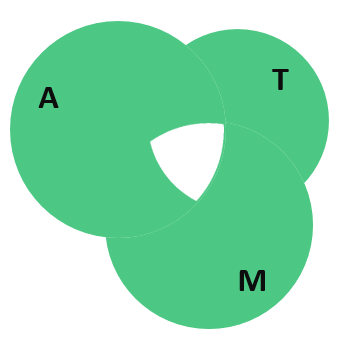
К счастью в незакрашенной области как раз и находятся те люди, число которых нам нужно посчитать. Действительно, эти бедняги используют ежедневно все три вида транспорта для того, чтобы добраться до работы, ведь они находятся на пересечении всех трёх множеств. Обозначим количество этих бедолаг за . Тогда диаграмма примет следующий вид:

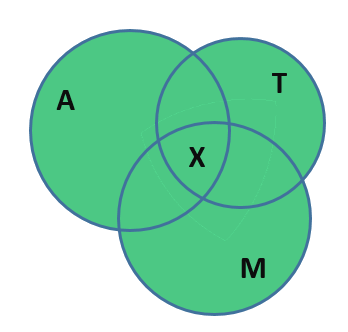
А уравнение станет следующим:

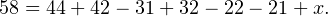
Расчёты дают . Это и есть ответ к задаче. Столько людей используют все три вида транспорта каждый день, чтобы добраться на работу.

Вот такое вот простое решение. Фактически, в одно уравнение. Просто удивительно, не правда ли?! А теперь представьте, как пришлось бы решать эту задачу без использования кругов Эйлера. Это было бы настоящее мучение. Так что в очередной раз убеждаемся, что любые методы визуализации чрезвычайно полезны при решении задач по математике. Используйте их, это поможет вам в решении сложных задач как на олимпиадах, так и на вступительных экзаменах по математике в лицеи и вузы.

Чтобы проверить, хорошо ли вы поняли решение данной задачи, ответьте на следующие вопросы:

1. Сколько человек используют только один вид транспорта для того, чтобы добраться до работы?
2. Сколько человек используют для этого ровно два вида транспорта?

В чем же суть?

На практике круги Эйлера, схема которых изображена ниже, могут применяться не только в математике, так как понятия «множества» присущи не только данной дисциплине. Так, они с успехом применяются и в менеджменте.

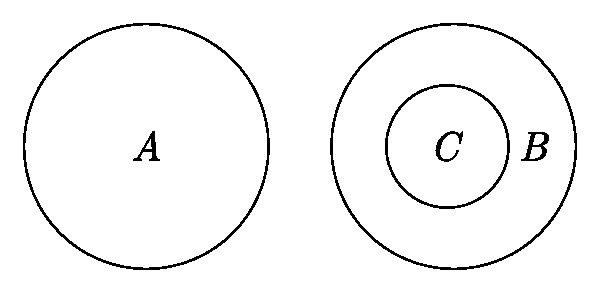
Схема выше показывает отношения множеств А (иррациональные числа), В (рациональные числа) и С (натуральные числа). Круги показывают, что множество С включено в множество В, тогда как множество А с ними никак не пересекается. Пример простейший, но наглядно объясняет специфику «взаимоотношений множеств», которые слишком абстрактны для реального сравнения хотя бы в силу их бесконечности.

Решение задач с помощью кругов Эйлера

Давайте рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.

Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Решение:

Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:

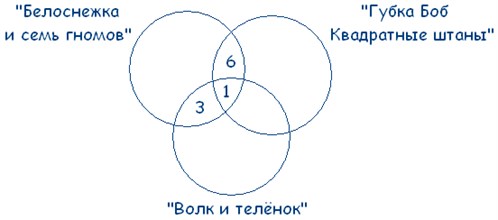
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:

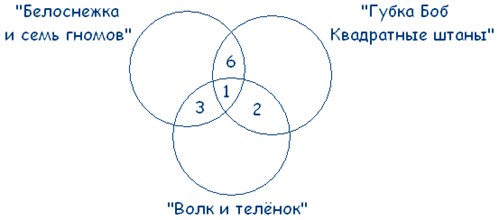
Выходит, что:

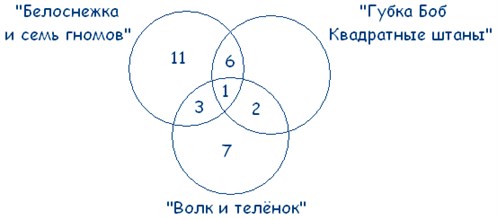
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».

13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».

Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Губка Боб Квадратные Штаны». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».

Теперь смело можем сложить все полученные цифры и выяснить, что:

мультфильм «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.

А еще давайте рассмотрим задачу, которая в 2011 году была вынесена на демонстрационный тест ЕГЭ по информатике и ИКТ (источник — http://eileracrugi.narod.ru/index/0-6).

Условия задачи:

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц (в тысячах)
Крейсер | Линкор	7000
Крейсер	4800
Линкор	4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?

Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.

Опираясь на условия задачи, составим уравнения:

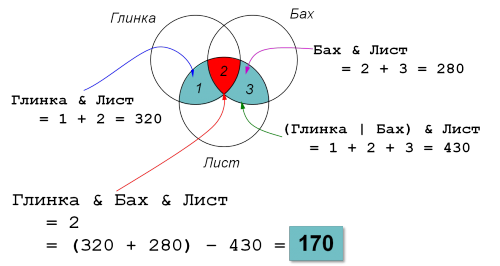
1. Крейсер | Линкор: 1 + 2 + 3 = 7000
2. Крейсер: 1 + 2 = 4800
3. Линкор: 2 + 3 = 4500

Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:

4800 + 3 = 7000, откуда получаем 3 = 2200.

Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:

2 + 2200 = 4500, откуда 2 = 2300.

Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор.

Как видите, круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

Алгебра логики

Данная область математической логики оперирует высказываниями, которые могут носить как истинный, так и ложный характер. Например, из элементарного: число 625 делится нацело на 25, число 625 делится нацело на 5, число 625 является простым. Первое и второе утверждения – истина, тогда как последнее – ложь. Конечно, на практике все сложнее, но суть показана ясно. И, конечно же, в решении опять участвуют круги Эйлера, примеры с их использованием слишком удобны и наглядны, чтобы их игнорировать.

Немного теории:

• Пусть множества А и В существуют и не являются пустыми, тогда для них определены следующие операции пересечения, объединения и отрицания.
• Пересечение множеств А и В состоит из элементов, что принадлежат одновременно как множеству А, так и множеству В.
• Объединение множеств А и В состоит из элементов, что принадлежат множеству А или множеству В.
• Отрицание множества А — это множество, что состоит из элементов, которые не принадлежат множеству А.

Все это изображают опять же круги Эйлера в логике, так как с их помощью каждая задача, вне зависимости от степени сложности, становится очевидной и наглядной.

Отношения между множествами

Также следует различать понятия элементов и множества, объем которых отображают круги Эйлера. Понятие множества заимствовано из математической науки и имеет достаточно широкое значение. Примеры в логике и математике отображают его как некую совокупность объектов. Сами же объекты являются элементами данного множества. «Множество есть многое, мыслимое как единое» (Георг Кантор, основатель теории множеств).

Обозначение множеств осуществляется заглавными буквами: А, В, С, D… и т. д., элементов множеств – строчными: а, b, с, d…и др. Примерами множества могут быть студенты, находящиеся в одной аудитории, книги, стоящие на определенной полке (или, например, все книги в какой-либо определенной библиотеке), страницы в ежедневнике, ягоды на лесной поляне и т. д.

В свою очередь, если определенное множество не содержит ни одного элемента, то его называют пустым и обозначают знаком Ø. Например, множество точек пересечения параллельных прямых, множество решений уравнения х2 = -5.

Объяснение заданий 17 ЕГЭ по информатике

17-я тема — «Логические выражения и запросы для поисковых систем» — характеризуется, как задания повышенного уровня сложности, время выполнения – примерно 2 минуты, максимальный балл — 1

Логические выражения и запросы для поисковых систем

• Таблицы истинности и порядок выполнения операций
• Поисковые запросы:
• операция «И» в поисковом запросе всегда ограничивает поиск (уменьшает количество страниц в выдаче), т. е., в ответ на запрос яблоко И груша поисковый сервер выдаст меньше страниц, чем на запрос яблоко, потому что будет искать страницы, на которых присутствуют оба этих слова;
• операция «ИЛИ» в поисковом запросе всегда расширяет поиск (увеличивает количество страниц в выдаче), т. е., в ответ на запрос яблоко ИЛИ груша поисковик выдаст больше страниц, чем на запрос яблоко, потому что будет искать страницы, на которых присутствует хотя бы одно из этих слов (или сразу оба слова);
• если в запросе присутствует фраза, заключенная в кавычки, то поисковик будет искать страницы с точно такой же фразой, а не просто отдельные слова из этой фразы; взятие словосочетания в кавычки ограничивает поиск, то есть, в ответ на запрос «яблоко груша» поисковик выдаст меньше страниц, чем на запрос яблоко груша, потому что поиск будет осуществляться только среди тех страниц, на которых эти слова стоят одно за другим.

Круги Эйлера

Большинство задач, связанных с поисковыми запросами, проще решать, используя круги Эйлера.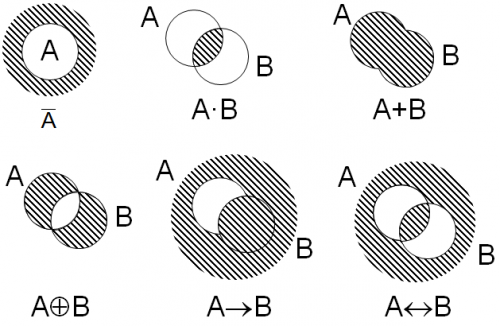

Пример использования кругов Эйлера:

Пример:
Известно количество сайтов, которых находит поисковый сервер по следующим запросам :

Ключевое слово	Количество сайтов, для которых данное слово является ключевым
Глинка & Лист	320
Бах & Лист	280
(Глинка | Бах) & Лист	430

Сколько сайтов будет найдено по запросу

Глинка & Бах & Лист

Вставка круга

1. На верней панели открываете вкладку Вставка.
2. В группе Иллюстрации нажимаете кнопку Фигуры и выбираете объект Овал.

1. Рисуете указателем мышки овал в нужном месте документа, а чтобы он автоматически становился кругом, одновременно зажмите и удерживайте клавишу Shift на клавиатуре.

Таким образом, получается ровная геометрическая фигура произвольного размера.

Чтобы нарисовать круг нужного диаметра, необходимо проделать 2 шага:

Шаг 1. Выделяете щелчком мыши нарисованное изображение.

Шаг 2. Переходите в раздел Средства рисования и вводите вручную в поле Размер высоту и ширину. К примеру нарисован объект диаметром 4 см.

Если вы хотите нарисовать круг и вставить туда текст или нарисовать круг с цифрой внутри, то потребуется сделать следующее:

1. Кликаете правой кнопкой мыши на иллюстрацию и выбираете функцию Добавить текст.

1. Добавляете внутрь изображения слова или цифру, а далее редактируете подходящий размер, шрифт, цвет, стиль и т.д.

Совместимые и несовместимые понятия

Под понятием в логике подразумевается форма мышления, отражающая существенные признаки класса однородных предметов. Они обозначаются одним либо группой слов: «карта мира», «доминантовый квинтсептаккорд», «понедельник» и др.

В случае когда элементы объема одного понятия полностью или частично принадлежат объему другого, говорят о совместимых понятиях. Если же ни один элемент объема определенного понятия не принадлежит к объему другого, мы имеем место с несовместимыми понятиями.

В свою очередь, каждый из видов понятий имеет собственный набор возможных отношений. Для совместимых понятий это следующие:

• тождество (равнозначность) объемов;
• пересечение (частичное совпадение) объемов;
• подчинение (субординация).

Для несовместимых:

• соподчинение (координация);
• противоположность (контрарность);
• противоречие (контрадикторность).

Схематически отношения между понятиями в логике принято обозначать при помощи кругов Эйлера-Венна.

Занимательная задача — «Кто?»

В редакции работают главный редактор, корректор, верстальщик, заместитель редактора и рядовой журналист.

Их фамилии – Ковалева, Кричковская, Иванченко, Мотыга и Тюлька.

Когда корректор и журналист учились в лингвистическом ВУЗе, они снимали вместе квартиру. Главный редактор на данный момент человек не семейный. Тюлька и Ковалева – неприятели. Муж Иванченко очень обрадовался, когда узнал, что главред разрешил его жене взять очередной отпуск в августе. Мотыга расстроился, когда узнал от главного редактора, что верстальщик и корректор скоро сыграют свадьбу. Ковалева и Кричковская пока еще не замужем.

Вопрос: какая фамилия у каждого сотрудника редакции?

Ответ	Показать ответ>

Резюме

Круги Эйлера – это очень полезная методика решения задач и установления логических связей, а заодно и занимательный и интересный способ провести время и потренировать мозг. Так что, если вам хочется совместить приятное с полезным и поработать головой, предлагаем пройти наш курс «Нейробика», включающий в себя самые разные задания, в том числе и круги Эйлера, эффективность которых научно обоснована и подтверждена многолетней практикой.

Круги Эйлера, на самом деле, достаточно часто встречаются в нашей жизни. Еще в младшей школе ученики начинают работать со схематическими фигурами, которые наглядно объясняют соотношения предметов и понятий.

Решение заданий 17 ЕГЭ по информатике

Задание 17 ЕГЭ по информатике 2017 ФИПИ вариант 1 (Крылов С.С., Чуркина Т.Е. «Типовые экзаменационные варианты»):
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».

 
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:

Запрос	Найдено страниц (в тысячах)
Пьер & Наука	180
Пьер & (Наука | Кюри)	410
Пьер & Кюри	320

Какое количество страниц (в тысячах) будет найдено по запросу:

Пьер & Наука & Кюри

Решение:

• Везде присутствует сомножитель «Пьер &» (и в искомом запросе!), сократим его:

Запрос	Найдено страниц (в тысячах)
Наука	180
Наука | Кюри	410
Кюри	320

Искомый запрос: Наука & Кюри

Используем круги Эйлера для решения, обозначив цифрами каждую составляющую:

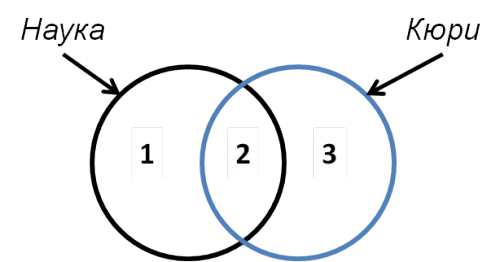
Из схемы и исходных данных получим:

1. №1 + №2 = 180 (Наука)
2. №2 + №3 = 320 (Кюри)
3. №1 + №2 + №3 = 410 (Наука | Кюри)

Сделаем подстановку в п.3 из п.1 и получим:

№1 + №2 + №3 = 180 + №3 = 410
№3 = 410 - 180 = 230

Сделаем подстановку в п.2:

№2 + №3 = №2 + 230 = 320
№2 = 320 - 230 = 90

Результат: 90

Детальный разбор данного задания 17 ЕГЭ по информатике предлагаем посмотреть в видео:

17 задание. Демоверсия ЕГЭ 2018 информатика:

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».

 
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:

Запрос	Найдено страниц (в сотнях тысяч)
Бабочка	22
Гусеница	40
Трактор	24
Трактор | Бабочка | Гусеница	66
Трактор & Гусеница	12
Трактор & Бабочка

Какое количество страниц (в сотнях тысяч) будет найдено по запросу

Бабочка & Гусеница?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

• Поскольку запрос Трактор & Бабочка возвращает значение 0, это значит, что в схеме кругов Эйлера-Вена два данных сектора пересекаться НЕ будут! Учитывая данный факт, отобразим круги Эйлера для решения, обозначив цифрами каждую составляющую:

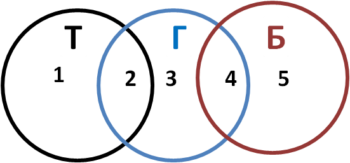
Получим значения отдельных секторов схемы, исходя из условий задачи:

1. №4 + №5 = 22
2. №2 + №3 + №4 = 40
3. №1 + №2 = 24
4. №1 + №2 + №3 + №4 + №5 = 66
5. №2 = 12

Искомый запрос: №4 = ?

№4 можно было бы выразить из п.1, если бы мы знали значение №5:

№4 + №5 = 22  ->
№4 = 22 - №5

№5 можно было бы найти из п.4, если бы мы знали значение №1:

№1 + №2 + №3 + №4 + №5 = 66  ->
№5 = 66 - №1 - (№2 + №3 + №4)
из пунктов 4 и 2:
№5 = 66 - №1 - 40 

Вычислим значение №1 из п.2 и п.5:

№2 = 12
№1 + №2 = 24  ->
№1 = 24 - 12 = 12

Теперь можно найти №5:

№5 = 66 - №1 - 40  ->
№5 = 66 - 12 - 40 = 14

Найдем №4:

№4 = 22 - №5  ->
№4 = 22 - 14 = 8

Результат: 8

Подробное решение 17 задания демоверсии ЕГЭ 2018 года смотрите на видео:

Решение задач

Для решения большого количества задач активно используются круги Эйлера. Примеры в логике наглядно демонстрируют связь логических операций с теорией множеств. При этом используются таблицы истинности понятий. Например, круг, обозначенный именем А, представляет собой область истинности. Таким образом, область вне круга будет представлять ложь. Чтобы определить область диаграммы для логической операции, следует заштриховать области, определяющие круг Эйлера, в которых ее значения для элементов А и В будут истинны.

Использование кругов Эйлера нашло широкое практическое применение в разных отраслях. Например, в ситуации с профессиональным выбором. Если субъект озабочен выбором будущей профессии, он может руководствоваться следующими критериями:

W – что я люблю делать?

D – что у меня получается?

P – чем я смогу хорошо зарабатывать?

Изобразим это в виде схемы: круги Эйлера (примеры в логике – отношение пересечения):

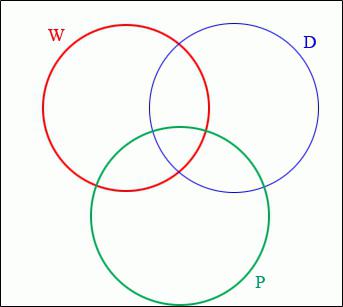
Результатом станут те профессии, которые окажутся на пересечении всех трех кругов.

Отдельное место круги Эйлера-Венна занимают в математике (теория множеств) при вычислении комбинаций и свойств. Круги Эйлера множества элементов заключены в изображении прямоугольника, обозначающего универсальное множество (U). Вместо кругов также могут использоваться другие замкнутые фигуры, но суть от этого не меняется. Фигуры пересекаются между собой, согласно условиям задачи (в наиболее общем случае). Также данные фигуры должны быть обозначены соответствующим образом. В качестве элементов рассматриваемых множеств могут выступать точки, расположенные внутри различных сегментов диаграммы. На ее основе можно заштриховать конкретные области, обозначив тем самым вновь образованные множества.

С данными множествами допустимо выполнение основных математических операций: сложение (сумма множеств элементов), вычитание (разность), умножение (произведение). Кроме того, благодаря диаграммам Эйлера-Венна можно проводить операции сравнения множеств по числу входящих в них элементов, не считая их.

Решение задач, примеры

Круги Эйлера и как решать сложные логические задачи, используя свойства диаграммы, можно показать на примерах.

Задача 1. Пусть имеется следующее условие: 54 школьника шестых классов занимаются в авиамодельном, музыкальном и танцевальном кружках. Каждый посещает хотя бы один кружок. Музыкой занимаются 32 ученика, 22 — танцами, 34 — авиамоделированием. Участвуют в музыкальном и танцевальном кружках 11 школьников, в музыкальном и авиамоделировании — 21, в танцевальном и авиамоделировании — 12. Сколько учащихся посещают все три кружка?

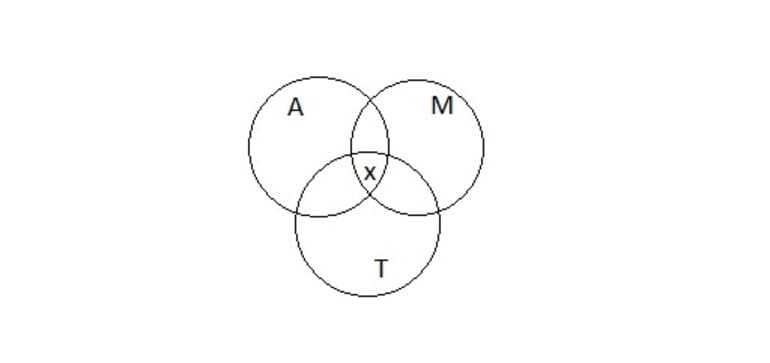
Рисунок 2

Проект решения предполагает необходимость расписать всех 54 школьников в соответствии с условиями задачи. Известно, что в авиамодельном кружке 34 ученика. Если прибавить к этому число учеников, которые занимаются музыкой, их 32 человека, то получится A ⋃ M, где ⋃ обозначение объединения множеств, будет состоять из 34 + 32… учеников.

Но при взгляде на круги Эйлера (Рисунок 2) становится понятно, что те, кто занимается и музыкой, и авиамоделированием посчитаны дважды. Это область на диаграмме, которая принадлежит и кругу A, и кругу М, таких учеников 21. Значит, объединение множеств A ⋃ M будет 34 + 32 — 21…

Теперь нужно прибавить 22 школьника, занимающихся танцами. A ⋃ M ⋃ T равно 34 + 32 — 21 + 22… Тут опять некоторые ученики оказываются посчитаны дважды. Можно вычесть из общей суммы тех, кто занимается танцами и музыкой — 11 человек и 12 человек, участвующих в авиамодельном и танцевальном кружках одновременно. Функция принимает следующий вид: A ⋃ M ⋃ T будет 34 + 32 — 21 + 22 — 11 — 12…

Но при этом школьники, которые посещают все три кружка, оказались отняты дважды. Их число обозначено x и его надо прибавить один раз к имеющейся формуле. Чтобы решить задачу, требуется определить x из полученного уравнения (Рисунок 3).

54 = 34 + 32 — 21 + 22 — 11 — 12 + х; откуда следует, что x = 10. Ответ: 10.

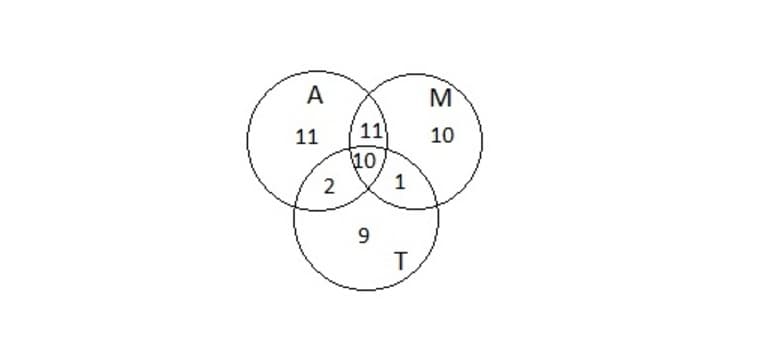
Рисунок 3

Задача 2. В школьную библиотеку пришло 30 учеников седьмого класса. Из них 15 человек взяли учебник по алгебре, 12 — по русскому языку, 10 человек не взяли ни одного учебника. Сколько учеников получили учебники по алгебре и русскому языку?

Множества на диаграммах представлены на рисунке 4. В большом круге 30 учеников, внутри двух малых 30 — 10 = 20 человек. По условию задачи 15 учеников получили учебник по алгебре, значит, 20 — 15 = 5 учеников получили только учебник по русскому языку. А в условии говорится, что 12 человек взяли учебник по русскому, то есть 12 — 5 = 7 школьников получили учебники и по алгебре, и по русскому. Ответ: 7.

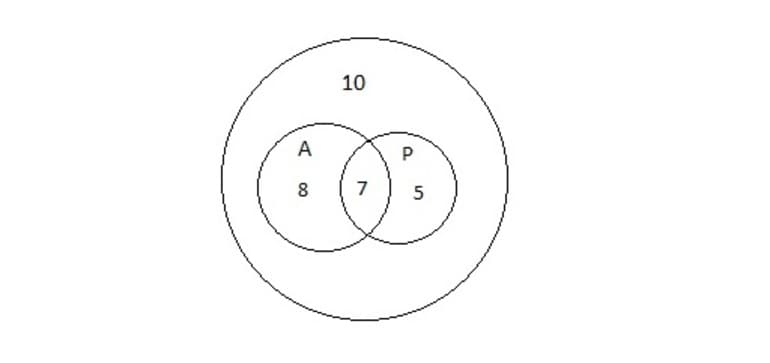
Рисунок 4

Круги Эйлера часто применяются для решения самых разных задач. Они служат для развития способности к логическому мышлению у дошкольников. Большой раздел задач для школьников может решаться с помощью диаграмм. Многие учёные в своих исследованиях тоже обращаются к этому методу, который повышает наглядность решаемых проблем и помогает в их обдумывании. Использование простых фигур позволяет свести решение любой сложной задачи к символической логике и упростить ход рассуждений. Диаграммы могут применяться и в обычной жизни, например при поиске работы. Пересечение кругов «лучше всего получается», «больше всего нравится делать» и «чем можно заработать», возможно, даст нужный результат.

Предыдущая
ИнформатикаКак сделать оглавление в ворде — алгоритм создания и примеры
Следующая
ИнформатикаФормула Шеннона — выводы, условия применения и примеры решения

Совместимые и несовместимые понятия

Под понятием в логике подразумевается форма мышления, отражающая существенные признаки класса однородных предметов. Они обозначаются одним либо группой слов: «карта мира», «доминантовый квинтсептаккорд», «понедельник» и др.

В случае когда элементы объема одного понятия полностью или частично принадлежат объему другого, говорят о совместимых понятиях. Если же ни один элемент объема определенного понятия не принадлежит к объему другого, мы имеем место с несовместимыми понятиями.

В свою очередь, каждый из видов понятий имеет собственный набор возможных отношений. Для совместимых понятий это следующие:

• тождество (равнозначность) объемов;
• пересечение (частичное совпадение) объемов;
• подчинение (субординация).

Для несовместимых:

• соподчинение (координация);
• противоположность (контрарность);
• противоречие (контрадикторность).

Схематически отношения между понятиями в логике принято обозначать при помощи кругов Эйлера-Венна.

Множества в математике

Диаграммы Венна помогают показать связь теории множеств и логических операций. Круги Эйлера, множества чисел и других предметов тесно связаны. Под множеством понимается совокупность каких-то объектов, называемых элементами. В множества можно объединять объекты с общим признаком. Например, множество студентов второго курса университета или множество статей, написанных одним учёным. Можно выделить три вида таких математических объектов:

• конечное, например, множество стран;
• бесконечное — множество звёзд во вселенной;
• пустое — множество острых углов в прямоугольнике.

В курсах информатики и обычно изучаются такие темы как «Введение в математическую логику» и «Поиск информации в Интернет». При решении задач по этим темам помощь оказывают диаграммы Венна. Для их построения можно использовать онлайн-калькулятор. Обозначения операций над множествами, которым должны соответствовать обозначения в калькуляторе:

• дополнение ¯A в калькуляторе имеет вид A’;
• пересечение A∩B представлено как A intersection B;
• объединение А⋃B обозначено A union B;
• симметрическая разность A∆B — symmetric difference of A and B;
• Относительное дополнение AB — AB.

Кольцом в теории множеств называют непустую систему R, замкнутую относительно пересечения и симметрической разности, то есть при пересечении или операции симметрической разности любых двух множеств обязательно получается множество, входящее в R. Это означает, что для любых элементов A, B из кольца элементы A∩B и A∆B будут лежать в кольце.

Отношения между понятиями

Логические операции, разрешающие доказывать утверждения и делать выводы, основаны на связях и отношениях разных понятий. При классификации понятия делятся на сравнимые, между которыми существуют логические связи и отношения, и несравнимые, которые не имеют связей. К несравнимым относятся, например, «машина» и «квадрат», «озеро» и «клетка». У них нет общих элементов и их нельзя сравнивать.

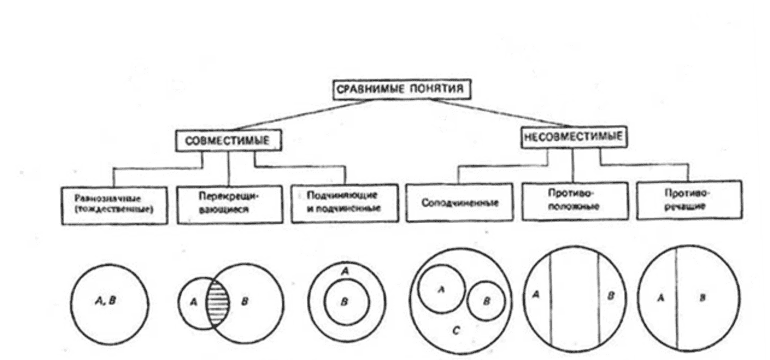
Рисунок 1

Сравнимые понятия подразделяются на совместимые и несовместимые. Совместимые понятия отличаются тем, что имеют хотя бы один общий элемент:

• равнозначные (тождественные);
• перекрещивающиеся;
• подчиняющие и подчинённые.

У равнозначных понятий объёмы полностью совпадают. Например, А — писатель Чехов, В — автор пьесы «Вишнёвый сад». Графически тождественность можно представить как два круга, слившиеся в один (Рисунок 1).

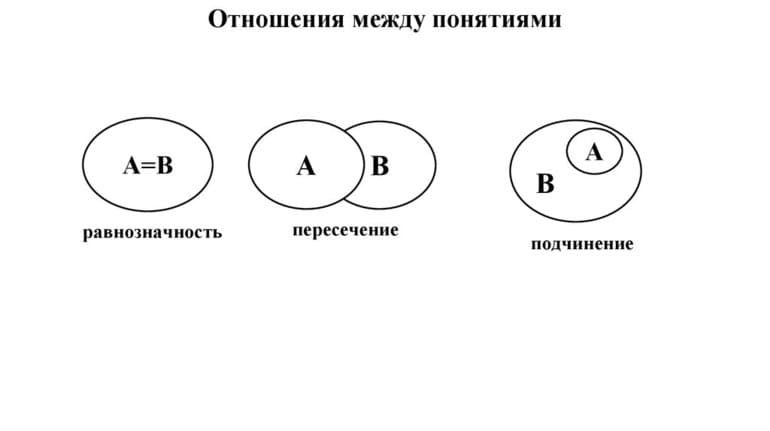
Пересекающимися понятиями, или находящимися в отношении перекрещивания, считаются те, объёмы которых совпадают частично. Пример: A — «математик», B — «репетитор»; A — «студент», B — «спортсмен». Часть объёма понятия «математик» входит в объём понятия «репетитор» и наоборот.

Понятия, состоящие в отношении подчинения, содержат одинаковые элементы, а объём подчинённого целиком входит в объём подчиняющего. Например, «млекопитающее» и «коза».

Несовместимыми называют понятия, не имеющие общих элементов:

• соподчинённые;
• противоположные;
• противоречащие.

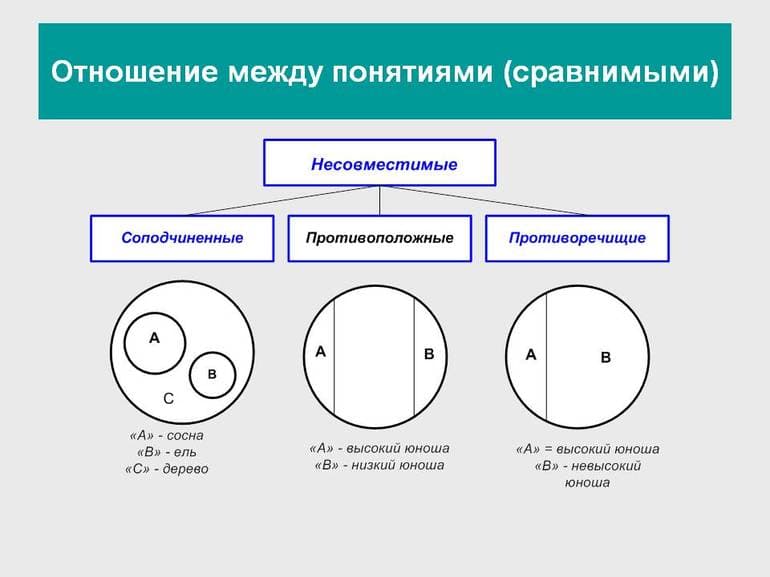
Соподчинённые понятия имеют общие элементы и вместе входят в родовое понятие, но в их объёмах общие элементы отсутствуют. Например, А — «корова», B — «овца», C — «млекопитающее». Круги A и B необходимо поместить внутри круга, изображающего объём понятия C, но они не смогут пересекаться, так как не бывает млекопитающих, которые были бы и коровой, и овцой одновременно.

Противоположные понятия — это виды одного и того же рода, но одно из них имеет какой-то признак, а другое не обладает им и содержит признак, несовместимый с первым, направленный против него. Таковы A — «большой дом» и B — «маленький дом». Тут в отличие от отношения противоречия возможны предметы, которые не входят ни в A и ни в B. Если общее родовое C — дом, то в его круге будут изображения двух сегментов A и B, расположенных напротив друг друга, а оставшаяся часть должна соответствовать всем остальным домам (средним, меньше средних).

Заключение

Полагаю, нам удалось убедить вас, что круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьный уроках, но и вполне себе житейских проблем. Выбора будущей профессии, например.

Вам еще наверняка будет любопытно узнать, что в современной массовой культуре круги Эйлера нашли отражение не только в виде мемов, но и в популярных сериалах. Таких, как «Теория большого взрыва» и «4исла».

Используйте это полезный и наглядный метод для решения задач. И обязательно расскажите о нем друзьям и одноклассникам. Для этого под статьей есть специальные кнопки.