Диаграмма сродства

Шпаргалка при подготовке презентаций с данными

Кемаев Олег (Kemaev Oleg)Follow

Nov 16, 2018 · 7 min read

При разработке большинства презентаций мы часто сталкиваемся с проблемой — не хватает времени на детальную проработку структуры и главной идеи.

А в презентациях-отчётах эта проблема усугубляется тем, что данные для представления собираются в последний момент. И когда данные собраны нужно быстро придумать как о них рассказать.

В таких ситуациях нам хочется “ухватиться за соломинку”, которая поможет выплыть в бушующем море дедлайнов. Заметка станет экспресс-помощью всем, делающим презы и визуализирующим данные. Сфокусируемся на пяти основных видах диаграмм и быстрых способах их выбора под задачу.

Для особо любознательных, в конце заметки есть краткий список литературы.

ПРИМЕР ДИАГРАММЫ СРОДСТВА #1

Производственная команда  использовала схему сходства для организации списка потенциальных показателей эффективности. На рисунке 1 показан список элементов. Поскольку команда работает по сменному графику, и участники не могут встретиться, чтобы сделать диаграмму сходства вместе, они изменили процедуру.

Рисунок 1 мозговой штурм для примера диаграммы сходства

Члены команды записывали каждую идею на стикеры и размещали их в случайном порядке на используемой двери. В течение нескольких дней все просматривали заметки и перемещали их в связанные группы. Некоторые люди пересматривали эволюционирующую модель несколько раз. Через несколько дней появилась естественная группировка, показанная на рисунке 2 (ниже).

Обратите внимание, что одна из заметок, “безопасность”, стала частью заголовка для своей группы. Остальные заголовки были добавлены после появления группы

Были определены пять основных направлений деятельности: качество продукции, техническое обслуживание оборудования, производственные затраты, объем производства, безопасность и охрана окружающей среды.

Рисунок 2 Пример Диаграммы Сходства

‍

‍

Позиционное сравнение

Здесь важна позиция, которую объект занимает по отношению к другим объектам. На сколько он больше или меньше других объектов, какое место занимает в “строю” других объектов. Для позиционного сравнения лучше подходит линейчатая диаграмма

При позиционном сравнении лучше подходит линейчатая диаграмма

В линейчатой диаграмме по вертикали располагаются обозначения сравниваемых элементов, шкала располагается горизонтально. Саму шкалу можно не отображать, а значения подписывать у линеек диаграммы (как на рисунке выше).

Линейчатая диаграмма подходит для позиционного сравнения лучше чем гистограмма. Нашим глазам привычнее позицию воспринимать по вертикали (вверху — лучше, внизу — хуже). А ещё, при таком расположении оси обозначений, появляется больше места для записи названий показателей.

Существует большое количество видов и способов использования линейчатых диаграмм. Но разбирать каждый пример не цель данной заметки, поэтому привожу только рисунок с шестью видами из книги.

рисунок взят из книги Джин Желязны «Говори на языке диаграмм»

Пример применения диаграммы сродства

Библиотека получает большое количество негативных отзывов клиентов о качестве обслуживания. Для анализа ситуации решили использовать диаграмму сродства. В состав группы были включены библиотекари. Участники эксперимента (шесть библиотекарей различного возраста, представляющих различные отделы библиотеки) сначала определили предмет исследования. Они формулировали его название с таким расчетом, чтобы получить в результате рекомендации для проведения мероприятий по повышению удовлетворенности обслуживанием клиентов библиотеки. После мозгового штурма доска со стикерами, наклеенными в случайном порядке, выглядела так, как показано на рисунке 1.

Рисунок 1. Идеи, расположенные в случайном порядке

После первой попытки сгруппировать идеи, длившейся примерно час, стало ясно, сразу сейчас это сделать не удастся: слишком много сил и энергии отнял мозговой штурм. Поэтому вся информация на доске сохранялась в неизменном виде в течение двух дней. Все это время библиотекари часто подходили к доске, чтобы изменить положение стикеров. Результирующая диаграмма сродства показана на рисунке 2.

Стрелки на диаграмме показывают связи между отдельными элементами, которые оказалось невозможным поместить в какую-либо группу. Это упражнение позволило разработать подходящие меры. Все имеющиеся идеи и решения были разбиты на группы (когорты), в которые включались идеи, имеющие внутренние связи.

Последующая работа была спланирована так, чтобы одновременно принималась во внимание только одна группа идей

Рисунок 2. Результат группировки идей по сродству

Просмотры:
5 677

Быстро: простые графики в Pandas

Pandas имеет встроенные функции построения графиков, которые можно вызывать непосредственно из Series и DataFrame. За что я обожаю эти функции, это за их краткость, за разумные значения по умолчанию и за то, что с их помощью можно быстро понять, что происходит с данными.

Для создания графика просто вызовите метод следующим образом:

np.exp(data==2018]).plot(
    kind='hist'
)

В результате выполнения этой команды получится следующий график:

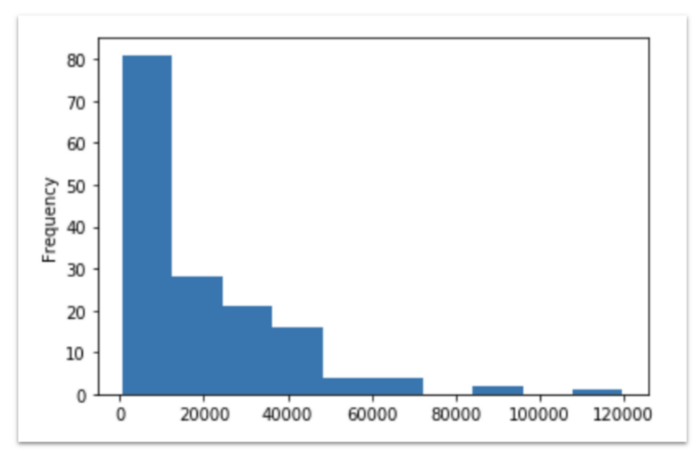
2018: Гистограмма количества стран в зависимости от ВВП на душу населения. Тут никаких сюрпризов: большинство стран бедны!

При построении графиков в Pandas я использую пять основных параметров:

• Pandas должна знать, какого типа график вы хотите строить. Возможны следующие варианты: .
• Позволяет переопределить значение размера, заданное по умолчанию (6 дюймов в ширину и 4 дюйма в высоту). Данный параметр принимает на вход кортеж, например , что я часто использую.
• Добавляет к графику заголовок. Как правило, я его использую, чтобы кратко описать, что происходит на графике, дабы потом это можно было быстро понять. Данный параметр принимает на вход строку.
• Позволяет переопределить ширину областей гистограммы. Данный параметр принимает на вход список или подобную ему последовательность, например .
• Позволяет переопределить максимальные и минимальные значения осей и . Оба параметра принимают на вход кортежи, например .

Давайте быстро пробежимся по некоторым типам таких графиков.

Вертикальная гистограмма

data == 2018
].set_index('Country name').nlargest(15).plot(
    kind='bar',
    figsize=(12,8)
)

2018: Список 15 самых счастливых стран в мире. Лидирует Финляндия.

Горизонтальная гистограмма

np.exp(data == 2018
].groupby('Continent')\
       .mean()).sort_values().plot(
    kind='barh',
    figsize=(12,8)
)

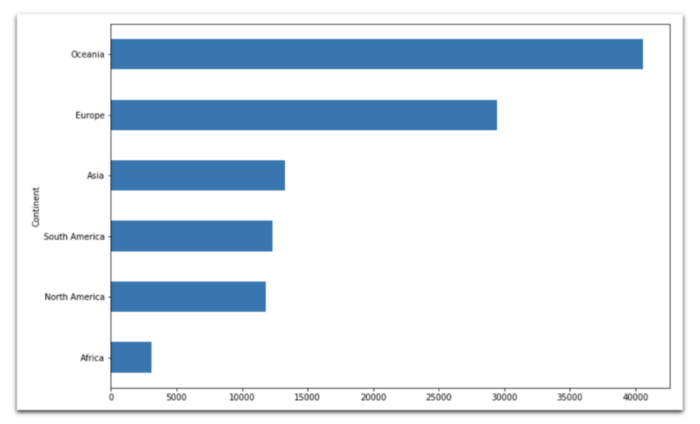
Средний ВВП на душу населения с разбивкой по континентам. Лидерство Австралии и Новой Зеландии неоспоримо.

Ящик с усами (Box plot)

data.plot(
    kind='box',
    figsize=(12,8)
)

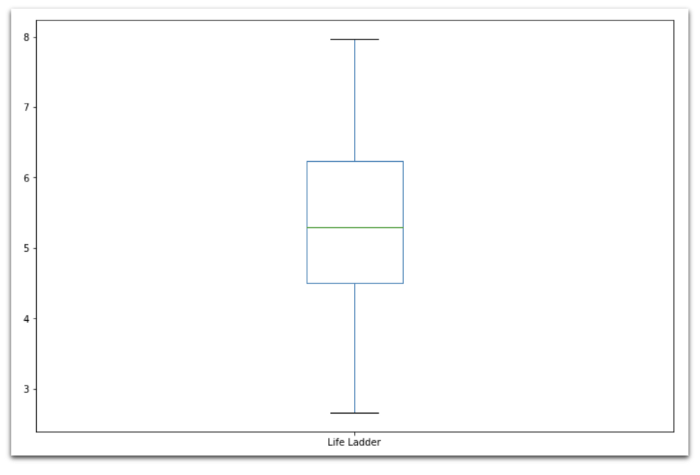
Распределение параметра Life Ladder («лестница жизни») показывает, что медианное значение «счастья» находится где-то в районе 5.5, и варьируется от 3 до 8.

Точечный график (диаграмма рассеяния)

data].plot(
    kind='scatter',
    x='Healthy life expectancy at birth',
    y='Gapminder Life Expectancy',
    figsize=(12,8)
)

Диаграмма рассеяния ожидания продолжительности здоровой жизни из Всемирного доклада о счастье (ось х) и ожидания продолжительности жизни из Gapminder (ось у) демонстрирует сильную корреляцию между этими данными (что не удивительно).

Гексбиновая диаграмма

data == 2018].plot(
    kind='hexbin',
    x='Healthy life expectancy at birth',
    y='Generosity',
    C='Life Ladder',
    gridsize=20,
    figsize=(12,8),
    cmap="Blues", # по умолчанию зеленый
    sharex=False # необходимо, чтобы не допустить ошибок
)

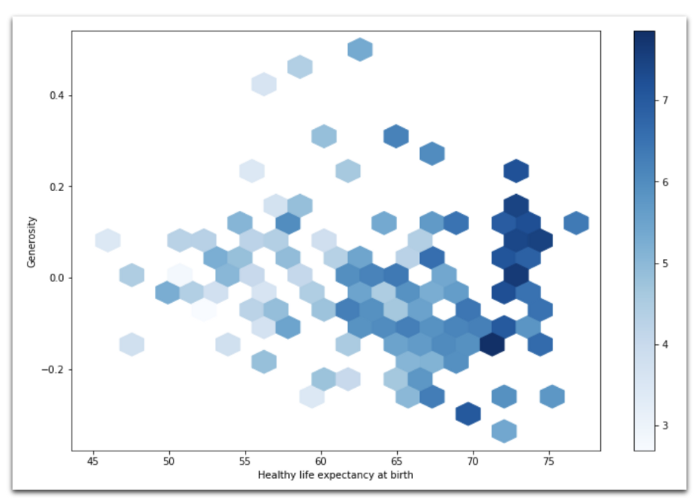
2018: Гексбиновая диаграмма показывает зависимость ожидаемой продолжительности жизни от щедрости.

Круговая диаграмма

data == 2018].groupby(
    
).sum().plot(
    kind='pie',
    figsize=(12,8),
    cmap="Blues_r", # по умолчанию оранжевый
)

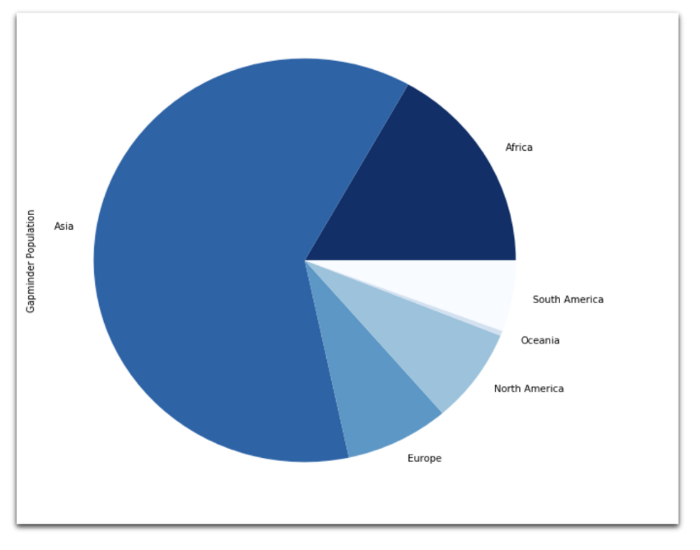
2018: Круговая диаграмма показывает количество жителей планеты с разбивкой по континентам.

Диаграмма с накоплением

data.groupby(
    
).sum().unstack().plot(
    kind='area',
    figsize=(12,8),
    cmap="Blues", # по умолчанию оранжевый
)

Количество жителей планеты растет.

Линейный график

data == 'Germany'
].set_index('Year').plot(
    kind='line',
    figsize=(12,8)
)

Динамика счастья в Германии.

Выводы

Строить графики в библиотеке pandas удобно, просто и быстро. Правда, они выходят слегка корявыми. Но это нормально, так как для создания более эстетичных графиков у нас есть другие инструменты. Переходим к библиотеке .

Очень красиво: потрясающие интерактивные графики в Plotly

И наконец-то, больше никакой Matplotlib! У библиотеки Plotly есть три важных свойства:

• «Зависание»: когда курсор «зависает» над графиком, всплывает окно с аннотацией.
• Интерактивность: графики легко могут быть сделаны интерактивными (то есть меняющимися во времени в зависимости от ваших действий) без каких-либо дополнительных настроек.
• Прекрасные геопространственные карты: в Plotly есть свои базовые инструменты для построения карт, однако для совершенного результата всегда можно воспользоваться интеграцией с Mapbox.

Точечный график (диаграмма рассеяния)

С помощью библиотеки Plotly графики строятся следующим образом. Создаем переменную , а затем запускаем функцию .

Логарифм подушевого ВВП

Точечный график (диаграмма рассеяния) — путешествие во времени

fig = px.scatter(
    data_frame=data, 
    x="Log GDP per capita", 
    y="Life Ladder", 
    animation_frame="Year", 
    animation_group="Country name",
    size="Gapminder Population", 
    color="Continent", 
    hover_name="Country name", 
    facet_col="Continent",
    size_max=45,
    category_orders={'Year':list(range(2007,2019))}     
)
fig.show()

Визуализация того, как данные меняются со временем.

Параллельные категории — прикольный способ визуализировать категоральные переменные

def q_bin_in_3(col):
    return pd.qcut(
        col,
        q=3,
        labels=
    )
_ = data.copy()
_ = _.groupby('Year').transform(q_bin_in_3)
_ = _.groupby('Year').transform(q_bin_in_3)
_ = _.groupby('Year').transform(q_bin_in_3)
_ = _.groupby('Year').transform(q_bin_in_3)
_ = _.groupby().mean().reset_index()
fig = px.parallel_categories(_, color="Life Ladder", color_continuous_scale=px.colors.sequential.Inferno)
fig.show()

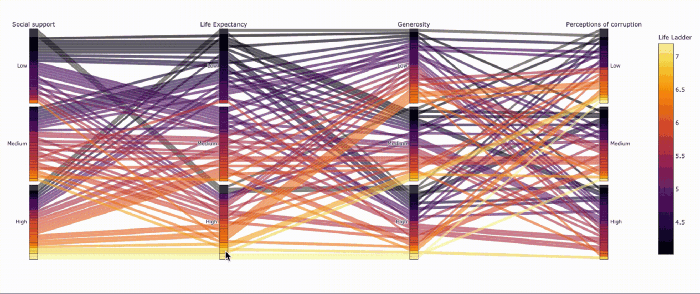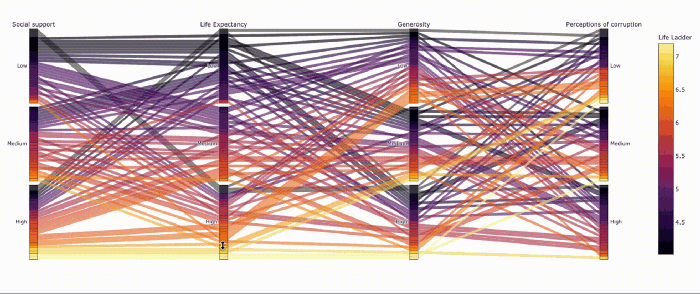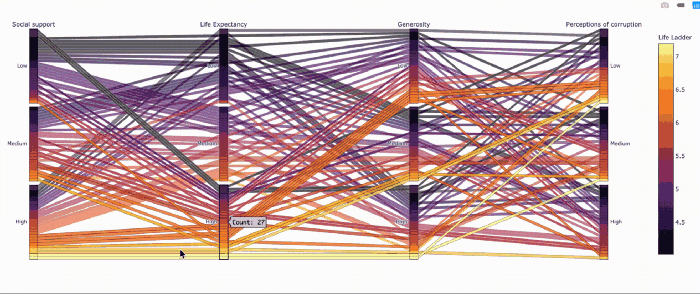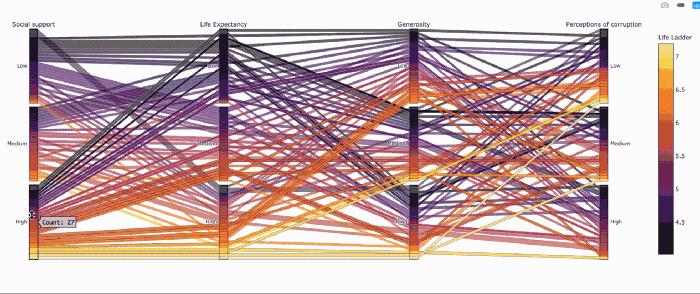
Похоже, не все страны с высокой продолжительностью жизни одинаково счастливы.

Столбчатые диаграммы — пример интерактивных фильтров

fig = px.bar(
    data, 
    x="Continent", 
    y="Gapminder Population", 
    color="Mean Log GDP per capita", 
    barmode="stack", 
    facet_col="Year",
    category_orders={"Year": range(2007,2019)},
    hover_name='Country name',
    hover_data=
)
fig.show()

Сюжетный график — как уровень счастья меняется со временем

fig = px.choropleth(
    data, 
    locations="ISO3", 
    color="Life Ladder", 
    hover_name="Country name", 
    animation_frame="Year")
fig.show()

Карта, визиолизирующая, как уровень счастья менялся со временем. Сирия и Афганистан в самом низу «лестницы счастья», что совсем не удивительно.

Частотное сравнение

Частотное сравнение используем когда нужно отобразить частоту попадания числовых значений в некий диапазон (интервал). Такое сравнение удобно использовать, когда нужно обобщить (суммировать) большой объём информации, чтобы показать какую-то взаимосвязь. Для визуализации частотного сравнения хорошо подходят гистограммы и графики

Используются две шкалы. Вертикальная — шкала частотности и горизонтальная — шкала диапазонов

Для шкалы диапазонов важно правильно подобрать размер и количество диапазонов (интервалов)

Через малое количество интервалов бывает трудно проследить модель распределения, а слишком большое количество разбивает модель на мелкие части. В среднем, для лучшего визуального восприятия, можно рекомендовать количество интервалов от 5 до 10.

Размеры интервалов надо подбирать так, чтобы нагляднее показать идею (главную мысль).

Варианты корреляции

Форма и расположение кластера точек на диаграмме разброса определяют различные варианты корреляции парных данных. Наиболее часто встречающиеся из них приведены на рисунках ниже.

Положительная (прямая) корреляция	Слабая положительная корреляция	Отсутствие корреляции
Отрицательная корреляция	Слабая отрицательная корреляция	Нелинейная корреляция

Диаграмма разброса является удобным и простым инструментом для выявления взаимосвязи парных данных. Однако сильная взаимосвязь не обязательно означает, что одна переменная напрямую связана с другой переменной. В частности, может быть третья переменная, которая влияет на исследуемые парные данные и которая в итоге «кластеризует» точки на диаграмме разброса.

Покомпонентное (долевое) сравнение

При таком сравнении мы показываем размер компонента в процентах от некоего целого. Целое обычно представляется в виде стандарта в 100%. При компонентном сравнении мы показывает долю от целого, поэтому его можно назвать и долевым сравнением. Круг у нас всегда ассоциируется с целым, поэтому для визуализации наиболее подходит круговая диаграмма.

При компонентном сравнении лучше подходит круговая диаграмма

Рекомендации по круговым диаграммам

Наши глаза не могут быстро определять количество объектов больше пяти. Секторов (долей) в диаграмме лучше не делать больше шести. Если значений больше, можно выделить пять основных, а остальные объединить в сектор “прочие”.

Мы привыкли по кругу двигаться по часовой стрелке

Самый важный компонент лучше располагать на линии 12-ти часов и обратить на него внимание выделив цветом. Если “важный” компонент выделять не надо, то сектора диаграммы лучше расположить от большего к меньшему

А цвет просто должен помогать чётко разделять сегменты.

Когда нужно сравнить компоненты (доли) нескольких целых, то лучше использовать гистограмму нормированную на 100%. В этом случае, самый важный показатель нужно размещать внизу.

Загрузка данных и импорт библиотек

Для начала давайте загрузим данные, которые мы будем использовать в этой статье. Я также произвел предобработку данных (интерполяцию и экстраполяцию — там, где это было уместно).

# загружаем данные
data = pd.read_csv('https://raw.githubusercontent.com/FBosler/AdvancedPlotting/master/combined_set.csv')
# присваиваем метки каждому году 
data  = data.groupby('Year').transform(
    pd.qcut,
    q=5,
    labels=()
)

Загруженный датасет содержит данные в следующих колонках:

• Year (год): год, в котором производились измерения (с 2007 по 2018).
• Life Ladder («лестница жизни»): респондент измеряет качество свой жизни по шкале от 0 до 10 (наилучшая оценка). Это так называемая лестница или шкала Кэнтрила.
• Log GDP per capita (логарифм ВВП на душу населения): ВВП на душу населения, подсчитанный по паритету покупательной способности доллара в 2011 году. Взято из индикаторов мирового развития (WDI — World Development Indicators), опубликованных Всемирным Банком 14 ноября 2018 года.
• Social support (социальная поддержка): Ответ на вопрос: «Если бы вы были в беде, то могли бы рассчитывать на помощь друзей или родственников или нет?»
• Healthy life expectancy at birth (ожидаемая продолжительность здоровой жизни): ожидаемое количество лет, в течение которых человек сможет вести активный образ жизни без всяких ограничений по здоровью. Показатели — на основе данных Всемирной организации здравоохранения (WHO — World Health Organization) за 2005, 2010, 2015 и 2016 годы.
• Freedom to make life choices (свобода делать жизненный выбор): Ответ на вопрос: «Удовлетворены ли вы вашим уровнем свободы выбирать, что делать со своей жизнью?»
• Generosity (щедрость): Ответ на вопрос: «Жертвовали ли вы деньги на благотворительность в прошлом месяце?» (в привязке к ВВП на душу населения).
• Perceptions of corruption (восприятие коррупции): Ответы на вопросы: «Широко ли распространена коррупция в правительственных кругах?» и «Широко ли распространена коррупция в бизнесе?»
• Positive affect (положительный аффект): включает в себя среднюю частоту счастья, смеха и радости в предыдущий день.
• Negative affect (отрицательный аффект): включает в себя среднюю частоту беспокойства, грусти и гнева в предыдущий день.
• Confidence in national government (доверие собственному правительству): не нуждается в пояснениях.
• Democratic Quality (качество демократии): насколько демократична страна.
• Delivery Quality (качество управления): насколько хорошо страна управляется.
• Gapminder Life Expectancy (продолжительность жизни от Gapminder): данные о продолжительности жизни от Gapminder.
• Gapminder Population (население страны от Gapminder): население страны.

4.5. Матричная диаграмма (таблица качества)

Матричная диаграмма — инструмент выявления важности различных связей. Такие матричные диаграммы (таблицы качества) часто называют сердцем «новых инструментов управления качеством» и QFD-методологии «дома качества». Матричную диаграмму используют для такой организации и представления большого количества данных (элементов), чтобы графически проиллюстрировать логические связи между различными элементами с одновременным отображением важности (силы) этих связей. Цель матричной диаграммы — табличное представление логических связей и относительной важности этих связей между большим количеством словесных (вербальных) описаний, имеющих отношение к следующему:задачам (проблемам) качества;причинам проблем качества;требованиям, установленным и предполагаемым потребностям потребителей;характеристикам и функциям продукции;характеристикам и функциям процессов;характеристикам и функциям производственных операций и оборудования. Матричная диаграмма выражает соответствие определенных факторов (и явлений) различным причинам их проявления и средствам устранения их последствий, а также показывает степень (силу) зависимости этих факторов от причин их возникновения и/или от мер по их устранению. Пример матричной диаграммы, часто называемой матрицей связей, приведен в табл

4.2. В табл. 4.2 использованы следующие обозначения:А (а1, а2, …, а6) — основные причины проблемы, представленные в виде компонентов а1, а2, аЗ, а4, а5, а6;В (b1, Ь2, ЬЗ,…, Ь7) — возможные средства для устранения последствий этих причин, изображенных в виде элементов (компонентов) b1, Ь2, ЬЗ, Ь4, Ь5, Ь6, Ь7.Символ который находится на пересечении строки и столбца матричной диаграммы, указывает не только на наличие связи между компонентами, но и на тесноту этой связи. Связь между компонентами А и В часто изображают в виде символов, характеризующих степень (силу) тесноты этих связей, например, ∆— слабая связь (1); О — средняя связь (3), ⊙ — сильная связь (9). Каждому из используемых в табл. 4.2 символов часто ставят в соответствие определенное значение весового коэффициента (как, например, указанные выше в скобках значения 1, 3 и 9). В некоторых случаях возникает необходимость в более подробном отображении силы (тесноты) связей. Тогда можно использовать следующие символы и весовые коэффициенты: Часто связь между факторами может быть как положительной, так и отрицательной. В этом случае можно рекомендовать для использования представленные ниже символы и весовые коэффициенты; В практической работе применяют различные по своей компоновке матрицы связей. Наибольшее распространение получили матричные диаграммы в виде L-, Т- и Х-карты, приведенные на рис. 4.7. Из рис. 4.7 видно, что L-, Т-, Х-карты получили такие названия, потому что выделенные более жирными линиями строки и столбцы напоминают:повернутую на -90° латинскую букву L;повернутую на +90° букву Т;повернутую на +45° букву X. Матричные диаграммы в виде L-карты применяют на практике наиболее часто, особенно при развертывании функции качества (QFD-методология, «дом качества»). Этим объясняется их второе назначение — таблицы качества. При практическом построении матричной диаграммы (в процессе работы команды качества) рекомендуется следующее:Рис. 4.7. Примеры различных форм матричных диаграмм: а — Ь-карта; б — Т-карта; в — Х-карта. С применением метода «мозговой атаки» («штурма») сформулируйте перечень компонентов (а1. а2, …. аn). (b, Ь2. …. Ьк), (с1, с2….cm).определяющих причины А, меры борьбы В с этими причинами и средства С, необходимые для достижения успеха.Составьте форму матричной диаграммы (таблицы качества) в виде L-, Т- или Х-карты и подготовьте (напечатайте) необходимое количество экземпляров таких таблиц. Предложите каждому участнику команды (кружка, группы) самостоятельно заполнить подготовленную таблицу качества символами, отображающими тесноту связи между рассматриваемыми компонентами. Сравните полученные результаты и в процессе обсуждения выработайтеобщее мнение (придите к консенсусу). Аккуратно оформите матрицу связей (таблицу качества) — результат работы команды. Не забудьте на этом документе указать сведения, которые позволят человеку, даже не принимавшему участия в работе команды, полностью понять и однозначно истолковать полученный результат. Для этого рядом с таблицей качества (матричной диаграммой) следует указать:название, местоположение (цех, участок) и основные характеристики объекта исследования;состав команды и ее руководителя;главные результаты работы;даты начала и окончания работы;любые другие сведения, достойные внимания.

Пример

1. Определяем цель составления матрицы приоритетов: уменьшить количество дефектов в изделии.

2. Формируем команду экспертов: для примера состав команды экспертов будет состоять из 3 человек. Каждый из них знаком с методом выработки решений на основе мозгового штурма.

3. Составляем список возможных решений проблемы: список решений поставленной проблемы сформированный командой экспертов.

изменить технологию изготовления;

увеличить число точек контроля;

провести обучение мастеров;

изменить конструкцию изделия;

4. Определяем состав критериев: состав критериев для оценки приоритетности решений.

требуется не более 100 чел\час на реализацию решения

низкая стоимость реализации решения

количество вовлекаемого персонала не более 50 чел.

снижение затрат на брак не менее чем в 1,5 раза.

5. Назначаем весовой коэффициент для каждого критерия. Рассмотри назначение критериев для каждого из 3-х методов — аналитического, метода консенсуса и матричного метода.

Для аналитического метода:

	Критерий	Весовой коэффициент
требуется не более 100 чел\час на реализацию решения	3
низкая стоимость реализации решения	9
количество вовлекаемого персонала не более 50 чел.	1
снижение затрат на брак не менее чем в 1,5 раза	9

Для метода консенсуса:

Устанавливаем, что каждый эксперт может распределить между критериями 4 балла.

Критерий	Эксперт 1	Эксперт 2	Эксперт 3	Весовой коэффициент
требуется не более 100 чел\час на реализацию решения	1	1
низкая стоимость реализации решения	2	3	1	6
количество вовлекаемого персонала не более 50 чел.	1	1
снижение затрат на брак не менее чем в 1,5 раза	1	3	4

Для матричного метода:

Критерии	требуется не более 100 чел\час на реализацию решения	низкая стоимость реализации решения	количество вовлекаемого персонала не более 50 чел.	снижение затрат на брак не менее чем в 1,5 раза	Итого
требуется не более 100 чел\час на реализацию решения	Х	1	1
низкая стоимость реализации решения	2	Х	2	1	5
количество вовлекаемого персонала не более 50 чел.	1	Х	1
снижение затрат на брак не менее чем в 1,5 раза	2	1	2	Х	5

6. Определяем наиболее значимые критерии: т.к. количество выбранных для примера критериев составляет всего 4, то оставляем все критерии.

7. Выбираем метод подсчета значимости каждого из предложенных ранее (на шаге 3) решений. Для определения значимости воспользуемся шкалой «1»-«3»-«9», где 9 — наиболее значимое решение, 3 — значимое решение, 1 — малозначимое решение.

8. Проведем оценку значимости кадого решения по отношению к каждому критерию: для оценки значимости решений воспользуемся аналитическим методом. Весовые коэффициенты критериев определены на шаге 5.

Решения	Критерии
требуется не более 100 чел\час на реализацию решения	низкая стоимость реализации решения	количество вовлекаемого персонала не более 50 чел.	снижение затрат на брак не менее чем в 1,5 раза
весовой коэффициент =3	весовой коэффициент =9	весовой коэффициент =1	весовой коэффициент =9
изменить технологию изготовления	3	1	1	9
увеличить число точек контроля	9	3	9	3
провести обучение мастеров	9	9	1	1
изменить конструкцию изделия	3	3	9	3

9. Определяем приоритетность каждого решения: оценка каждого решения перемножается на весовой коэффициент каждого критерия и значения суммируются.

Решения	Критерии	Итого
требуется не более 100 чел\час на реализацию решения	низкая стоимость реализации решения	количество вовлекаемого персонала не более 50 чел.	снижение затрат на брак не менее чем в 1,5 раза
весовой коэффициент =3	весовой коэффициент =9	весовой коэффициент =1	весовой коэффициент =9
изменить технологию изготовления	9	9	1	81	100
увеличить число точек контроля	27	27	9	27	90
провести обучение мастеров	27	81	1	9	119
изменить конструкцию изделия	9	27	9	27	72

10. Распределяем решения по порядку приоритетности:

1. Провести обучение мастеров — 118

2. Изменить технологию изготовления — 100

3. Увеличить число точек контроля — 90

4. Изменить конструкцию изделия — 72

Матрица приоритетов, по сравнению с другими метода ранжирования, дает возможность более объективно оценить значимость данных и установить величину этой значимости.

Вместе с тем, очевиден и недостаток этого инструмента качества – он достаточно трудоемкий, особенно когда необходимо провести ранжирование большого количества данных по большому количеству критериев.

Особенности метода

Диаграмма сродства

Рекомендации:

1. При формулировании темы для обсуждения использовать «правило 7 плюс или минус 2». Предложение должно иметь не менее 5 и не более 9 слов, включая глагол и существительное.
2. При проведении «мозговой атаки» использовать стандартную методику.
3. Каждая формулировка записывается на отдельную карточку.
4. Если карточка может быть отнесена больше чем к одной группировке, следует сделать копии.

Примечание. Карточки, не вошедшие ни в какую группировку, составляют остаток. Как правило, это 4 или 5 карточек.

Дополнительная информация:

Диаграмма сродства используется в работе не с конкретными числовыми данными, а со словесными высказываниями.

Диаграмму сродства следует применять, главным образом, когда:

• необходимо систематизировать большое количество информации (различных идей, разных точек зрения и т. д.);
• ответ или решение не всем абсолютно очевиден;
• принятие решения требует согласия среди членов команды (а воз- можно, и среди других заинтересованных лиц), чтобы эффективно работать.

Временное сравнение

Используем, когда надо продемонстрировать, как показатели (данные) меняются во времени (динамика изменений). В визуальном восприятии мы привыкли воспринимать время слева (прошлое), направо (будущее). При временном сравнении для визуализации данных лучше подходит гистограмма.

Здесь тоже можно руководствоваться правилом “не больше пяти”. То есть, если на временной оси нужно показать более 5 значений (столбиков), возможно лучше использовать график. График однозначно нужно использовать вместо диаграммы, если значений больше семи, или нужно отобразить какие-то тренды.

Если на графике нужно отобразить изменение нескольких показателей, то лучше не использовать более трёх линий тренда. При нескольких линиях тренда, линию главного показателя выделяем цветом или толщиной.

Как и в случае с линейчатыми диаграммами, у гистограмм тоже есть множество разновидностей, за подробностями ныряйте в список литературы.